c++实验4 栈及栈的应用+回文+中、后缀表达式

栈及栈的应用+回文+中、后缀表达式

1、栈顺序存储结构的基本操作算法实现

（1）栈顺序存储结构的类定义：

class SeqStack
{
private:
    int maxsize;
    DataType *data;      //顺序堆栈数组
    int top;                                            //栈顶位置指示器
public:
    SeqStack(int size);      //构造函数
    ~SeqStack(void) {}            //析构函数
    void Push(const DataType item);      //入栈
    DataType Pop(void);                  //出栈
    DataType GetTop(void)const;      //取栈顶数据元素
    void GetAll();
    void Destory();
    void ClearAll();
    int NotEmpty(void)const            //堆栈空否
    {return(top==-);};
    int Full(void)const             //堆栈满否
    {return(top==maxsize-);};
};

（2）构造栈算法

输入：栈元素个数的最大数size

初始化栈：栈顶指示置为-1，创建存储栈的数组，栈元素个数的最大数maxsize置 为size;

SeqStack::SeqStack(int size)
{
    top=-;
    maxsize=size;
    data=new DataType[maxsize];
}

（3）获得栈顶元素算法

输入：无

前置条件：栈不空

动作：取栈顶数据元素给e

输出：返回栈顶元素值e

后置条件：无

DataType SeqStack::GetTop(void)const           //取栈顶数据元素
//取当前栈顶数据元素并返回
{
    if(top==-)
    {
        cout<<"堆栈空!"<<endl;
        exit();
    }
    DataType e=data[top-];
    return e;                        //返回当前栈顶元素
}

（4）进栈算法

输入：要进栈的项item

前置条件：栈未满

动作：把item压入栈顶

输出：无

后置条件：栈顶增加一个新元素，栈顶指示加1;

void SeqStack::Push(const DataType item)       //入栈
//把元素item入栈;堆栈满时出错退出
{
    if(top==maxsize)
    {
        cout<<"堆栈已满!"<<endl;
        exit();
    }
    data[top]=item;                       //先存储item
    top++;                                //然后top加1
}

（5）出栈算法

输入：无

前置条件：栈非空

动作：删除栈顶元素

输出：返回删除的栈顶元素值

后置条件：删除栈顶元素，栈顶指示减1

DataType SeqStack::Pop()                       //出栈
//出栈并返回栈顶元素;堆栈空时出错退出
{
    if(top==-)
    {
        cout<<"堆栈已空!"<<endl;
        exit();
    }
    top--;                             //top先减1
    return data[top];                 //然后取元素返回
}

（6）遍历栈算法

输入：无

前置条件：栈非空

动作：遍历输出每个栈非空元素

输出：无

后置条件：无

void SeqStack::GetAll()
{
    if(top==-)
    {
        cout<<"堆栈已空!"<<endl;
        exit();
    }
    for(int i=top-;i>=-;i--)
    {
        cout<<data[i]<<" ";
    }
    cout<<endl;
}

（7）销毁栈算法

输入：无

前置条件：栈存在

动作：删除存储栈元素的数组

输出：无

后置条件：栈的存储元素区域不存在，栈顶指针归-1,maxsize为0

void SeqStack::Destory()
{
    top=-;

    delete data;
    cout<<"栈的存储元素区域不存在"<<endl;
    maxsize=;
}

（8）清空栈算法

输入：无

前置条件： 无

动作：清空栈，栈顶指示器归-1;

输出：无

后置条件：栈顶指示为-1

void SeqStack::ClearAll()
{
    top=-;
}

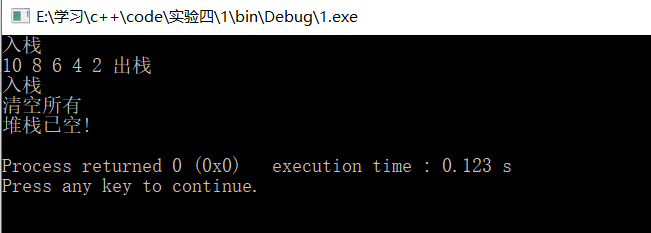
上机实现以上基本操作，写出main()程序：

#include <iostream>
typedef int DataType;
#include"SeqStack.h"
using namespace std;
int main()
{
    SeqStack stack1335();
    DataType test[]={,,,,};
    for(int i=;i<;i++)
        stack1335.Push(test[i]);
     cout<<"入栈"<<endl;
    while(!stack1335.NotEmpty())
        cout<<stack1335.Pop()<<" ";
    cout<<"出栈"<<endl;
    for(int i=;i<;i++)
        stack1335.Push(test[i]);
    cout<<"入栈"<<endl;
    stack1335.ClearAll();
    cout<<"清空所有"<<endl;
    stack1335.GetAll();
    return ;
}

2、用以上基本算法，实现：void conversion()

将输入10进制数转化为2进制和8进制数

void SeqStack::conversion(int num)
{
    int a=num;
    while(a)
    {
        Push(a%);
        a/=;
    }
    cout<<"转换为二进制：";
    GetAll();
    ClearAll();
    while(num)
    {
        Push(num%);
        num/=;
    }
     cout<<"转换为八进制：";
     GetAll();
　　}
} 

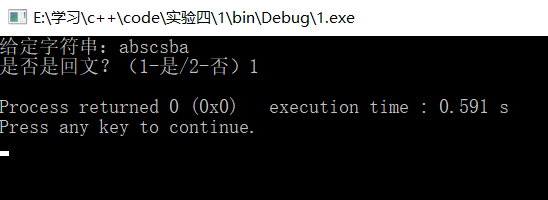
3、回文是指正读反读均相同的字符序列，如“acdca”、“dceecd”均是回文，但“book”不是回文。利用1中的基本算法，试写一个算法判定给定的字符串是否为回文。（提示：将一半字符入栈，依次弹出与另一半逐个比较）//判s串是否为回文，是则返回1，否则返回0;

int SeqStack::HuiWen(char *s)
{
    int i,j;
    for(i=;s[i]!='\0';i++);
    for(j=;j<(i-)/;j++)
    {
        Push(s[j]);
    }
    char ch= Pop();
    if(s[j]==ch)
    {
        for(int k=j;k<i-;i++)
        {
            if(s[k]!=Pop())
                return ;
        }
        return ;
    }

    else if(s[j+]==ch)
    {
        for(int k=j+;k<i-;k++)
        {
            if(s[k]!=Pop())
                return ;
        }
        return ;

     }
     else
        return ;
}
int main()
{
    SeqStack stack1335();
    char b[]={'a','b','s','c','s','b','a'};
cout<<"给定字符串："<<b<<"是否是回文？（1-是/2-否）"<<stack1335.HuiWen(b)<<endl;
}

4、实现栈的链式操作算法。

#include<stdlib.h>
#include<iostream>
using namespace std;
template<class T>
class LinStack;
template <class T>
class StackNode
{
    friend class LinStack<T>;
private:
    T data;
    StackNode<T> *next;
public:
    StackNode(StackNode<T> *ptrNext=NULL)
    {next=ptrNext;}
    StackNode(const T& item,StackNode<T> *ptrNext=NULL)
    {data=item;next=ptrNext;}
    ~StackNode(){}
};
template<class T>
class LinStack
{
private:
    StackNode<T>*head;
    int size;
public:
    LinStack(void);                           //构造函数
    ~LinStack(void);                          //析构函数
    void Push(const T& item);           //入栈
    T Pop(void);                                   //出栈
    T GetTop(void) const;                  //取栈顶元素
    int NotEmpty(void) const;             //堆栈非空否
};
template <class T>
LinStack <T>::LinStack()                    //构造函数
{
    head=new StackNode <T>;                 //头指针指向头结点
    size=;                                 //size的初值为0
}
template <class T>
LinStack <T>::~LinStack(void)               //析构函数
//释放所有动态申请的结点空间
{
    StackNode <T> *p,*q;
    p=head;                                 //p指向头结点
    while(p!=NULL)                          //循环释放结点空间
    {
        q=p;
        p=p->next;
        delete q;
    }
}
template <class T>
int LinStack <T>::NotEmpty(void) const      //堆栈非空否
{
    if(size!=)
        return ;
    else
        return ;
}
template <class T>
void LinStack <T>::Push(const T& item)      //入栈
{
    //新结点newNode的data域值为item,next域值为head->next
    StackNode <T> *newNode=new StackNode <T> (item,head->next);
    head->next=newNode;                    //新结点插入栈顶
    size++;                                //元素个数加1
}
template <class T>
T LinStack <T>::Pop(void)                  //出栈
{   if(size==)
    {
        cout<<"堆栈已空无元素可删!"<<endl;
        exit();
    }
    StackNode <T> *p=head->next;       //p指向栈顶元素结点
    T data=p->data;
    head->next=head->next->next;       //原栈顶元素结点脱链
    delete p;                          //释放原栈顶结点空间
    size--;                            //结点个数减1
    return data;                   //返回原栈顶结点的data域值
}
template <class T>
T LinStack <T>::GetTop(void) const         //取栈顶元素
{
    return head->next->data;
}

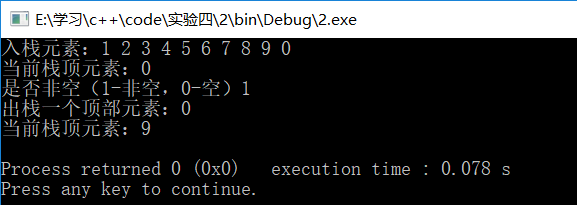
测试数据（main函数）

#include <iostream>
#include"LinStack.h"
using namespace std;

int main()
{
    int n[]={,,,,,,,,,};
    LinStack<int>li;
    cout<<"入栈元素：";
    for(int i=;i<;i++)
    {
        cout<<n[i]<<" ";
        li.Push(n[i]);
    }
    cout<<"\n当前栈顶元素："<<li.GetTop()<<endl;;
    cout<<"是否非空（1-非空，0-空）"<<li.NotEmpty()<<endl;
    cout<<"出栈一个顶部元素："<<li.Pop()<<endl;;
    cout<<"当前栈顶元素："<<li.GetTop()<<endl;;
    return ;
}

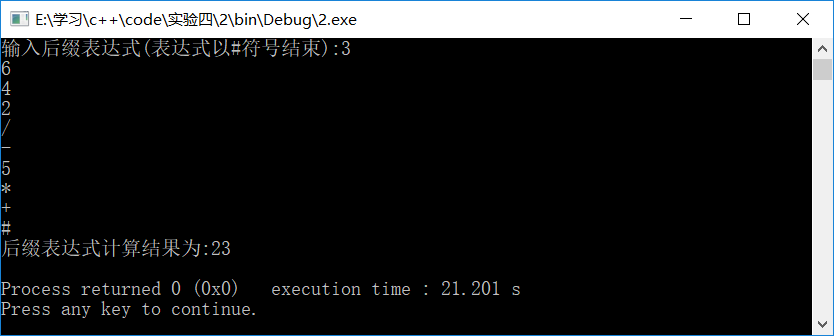
5、实现后缀表达式求值Eval(postexp e)算法。

#include <iostream>
#include<ctype.h>
#include<stdlib.h>
#include"LinStack.h"
template <class T>
void PostExp(LinStack <T> &s)
{
    char ch;           //ch为char类型变量
    T x,x1,x2;
    cout<<"输入后缀表达式(表达式以#符号结束):";
    while(cin>>ch&&ch!='#')   //循环直到输入为'#'
    {
        if(isdigit(ch))       //ch为数字类型
        {
            cin.putback(ch);  //回退一位
            cin>>x;           //按数值类型重新输入
            s.Push(x);        //x入栈
        }
        else
        {
            x2=s.Pop();       //退栈得操作数
            x1=s.Pop();       //退栈得被操作数
            switch(ch)
            {
            case'+':{x1+=x2;break;}
            case'-':{x1-=x2;break;}
            case'*':{x1*=x2;break;}
            case'/':
                if(x2==0.0)
                {
                    cout<<"除数为0错!";
                    exit();
                }
                else
                {
                    x1/=x2;
                    break;
                }
            }
             s.Push(x1);        //运算结果入栈
          }
    }
    cout<<"后缀表达式计算结果为:"<<s.Pop()<<endl;
}
using namespace std;
int main()
{

    LinStack<int>li;
　　 PostExp(li);
}

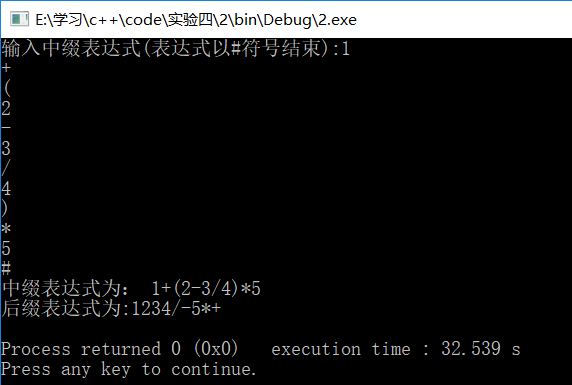
6、实现中缀表达式转换成后缀表达式postfix(expression e)算法

void error()
{
     cout<<"输入有误 退出"<<endl;
     exit();
}
template <class T>
int PostFix(LinStack <T> &s)
{
    string a,b;
    char ch;           //ch为char类型变量
    T x1,x2=' ';
    s.Push('#');
    cout<<"输入中缀表达式(表达式以#符号结束):";
    int flag=;
    while(true)   //循环直到输入为'#'
    {
        if(x2!='#'&&flag==)
        {
            b+=ch;
            cin>>ch;
        }
        if(!isdigit(ch))       //ch不为数字类型
        {
            x1=s.GetTop();
            x2=ch;
            if(x2==')')
                flag=;
            if(x1=='+'||x1=='-')
            {
                if(x2=='+'||x2=='-'||x2==')'||x2=='#')
                {
                    a+=s.Pop();
                }
                else if(x2=='*'||x2=='/'||x2=='(')
                    s.Push(x2);
                else
                    error();
            }
             if(x1=='*'||x1=='/')
            {
                if(x2=='+'||x2=='-'||x2==')'||x2=='#'||x2=='*'||x2=='/')
                     a+=s.Pop();
                else if(x2=='(')
                    s.Push(x2);
                else
                    error();
            }
            if(x1=='(')
            {
                if(x2==')')
                {
                    s.Pop();
                    flag=;
                }

                else if(x2=='+'||x2=='-'||x2=='*'||x2=='/'||x2=='(')
                    s.Push(x2);
                 else
                     error();
            }
             if(x1==')')
            {
                if(x2=='+'||x2=='-'||x2=='*'||x2=='/'||x2==')'||x2=='#')
                    a+=s.Pop();
                 else
                     error();

            }
             if(x1=='#')
            {
                if(x2=='+'||x2=='-'||x2=='*'||x2=='/'||x2=='(')
                {
                    s.Push(x2);
                }
                else if(x2=='#')
                {
                    cout<<"中缀表达式为："<<b<<"\n后缀表达式为:"<<a<<endl;
                    return ;
                }
                else
                     error();
            }
        }
        else                    //ch是数字
        {
            a+=ch;
        }
    }
}

测试函数（main函数）

主函数
int main()
{

    LinStack<int>li;
　　 PostFix(li);
}