luoguP4284 [SHOI2014]概率充电器 概率期望树形DP

这是一道告诉我概率没有想象中那么难的题.....

首先，用期望的线性性质，那么答案为所有点有电的概率和

发现一个点的有电的概率来源形成了一个"或"关系，在概率中，这并不好计算...（其实是可以算的，只不过式子要复杂点...）

考虑反面，一个点没电的概率来源是一个“与”关系，比较好计算

举个荔枝，有$A, B, C$三个变量，$A, B, C$分别有$0.5, 0.3, 0.2$的概率为$1$

问$A | B | C$为$1$的概率？

如果，我们从正面考虑，那么答案为$0.5 + (1 - 0.5) * 0.3 + (1 - 0.5 - (1 - 0.5) * 0.3) * 0.2 = 0.72$

但是，如果从反面考虑，那么答案为$1 - (1 - 0.2)(1 - 0.3)(1 - 0.5) = 0.72$

从这个荔枝可以看出，概率中“或”很难算，“与”比较好算（其实求解$| = !\&!$）

那么，考虑一个点没电，大体上分为子树不给电和父亲不给电两种情况

分别来考虑：

记$i$自己用爱发电的概率为$e_i$，边$(u, v)$用爱发电的概率为$e(u, v)$

设子树内不给$u$充电的概率为$f[u]$，那么$f[u] = (1 - e_i) * \prod_{v \in son_u} f[v] + (1 - f[v]) * (1 - e(u, v))$

再来考虑父亲不给电

设父亲不给$u$充电的为$g[u]$，那么有$g[u] = g[fa] + (1 - g[fa])(1 - e(u, fa))$

那么，求解$g[fa]$就成了一个问题，如果我们在$O(n ^2 )$的时间内求出所有的$g[fa]$，那么我们就能在$O(n ^ 2)$求出所有的$f$

在$O(n ^ 2)$的时间内求出$g[fa]$，自然是不难的，发现这是一个以$fa$为根的$dp$

对于一个节点，$f[u] *g[u]$就是答案

进一步分析，发现其实求$g[fa]$的时候非常的状态是重复的，能不能优化呢？

当然是可以的，画个美妙的图

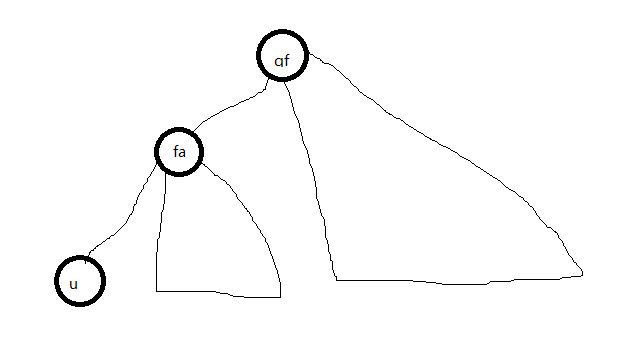
那么，注意到以$fa$为根的子树包括$gf$的子树和$fa$除了$u$以外的子树

那么，只要能快速地调用除了$u$以外的所有子树转移值得乘积，就能解决左边的子树

同时，右边的子树可以调用$g[gf]$来快速转移

然后就是$O(n)$啦!

代码好像还加了点优化

年代久远了，忘了是什么优化了...

#include <cstdio>
#define dl double
#define sid 500050
#define ri register int
using namespace std;

char RR[];
extern inline char gc() {
    static char *S = RR + , *T = RR + ;
    if(S == T) fread(RR, , , stdin), S = RR;
    return *S ++;
}
inline int read() {
    int p = , w = ; char c = gc();
    while(c > '' || c < '') { if(c == '-') w = -; c = gc(); }
    while(c >= '' && c <= '') { p = p *  + c - ''; c = gc(); }
    return p * w;
}

int n, cnt;
dl a[sid], s[sid], f[sid], pi[sid * ];
int cap[sid], node[sid * ], nxt[sid * ];

void addedge(int u, int v, dl p) {
    nxt[++ cnt] = cap[u]; cap[u] = cnt;
    node[cnt] = v; pi[cnt] = 1.0 - p;
}

void son_fa(int e, int fa) {
    s[e] =  - a[e];
    for(int i = cap[e]; i; i = nxt[i]) {
        int d = node[i];
        if(fa == d) continue;
        son_fa(d, e);
        s[e] *= s[d] + ( - s[d]) * pi[i];
    }
}

void fa_son(int e, int fa) {
    for(int i = cap[e]; i; i = nxt[i]) {
        int d = node[i];
        if(d == fa) continue;
        dl P = f[e] / (s[d] + ( - s[d]) * pi[i]);
        f[d] = (P + ( - P) * pi[i]) * s[d];
        fa_son(d, e);
    }
}

int main() {
    n = read();
    for(ri i = ; i < n; i ++) {
        int u = read(), v = read(), p = read();
        addedge(u, v, p / 100.0); addedge(v, u, p / 100.0);
    }
    for(ri i = ; i <= n; i ++) {
        int p = read();
        a[i] = p / 100.0;
    }
    son_fa(, );
    f[] = s[];
    fa_son(, );
    dl ans = ;
    for(ri i = ; i <= n; i ++) ans +=  - f[i];
    printf("%.6lf\n", ans);
    return ;
}