JAVA数据结构--优先队列（堆实现）

优先队列（堆）的定义

堆（英语：Heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。在队列中，调度程序反复提取队列中第一个作业并运行，因为实际情况中某些时间较短的任务将等待很长时间才能结束，或者某些不短小，但具有重要性的作业，同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。

我个人比较通俗的理解就是比如我们平常下载视频看，我们打算下载两部视频，一部2G，一部只有200M。优先队列的思想就是先下载那部体积较小的视频，这样也比较合理，可以下完200M后看的同时再下2G的视频。

堆是一颗被完全填满的二叉树，唯一可能的例外是在最底层。所以堆具有两个性质——堆序性和结构性。一个高为h的完全二叉树有2^h或2^h-1个节点，并且堆中每一个节点X的父亲的值小于或等于X中的关键字，所以堆的最小值总可以在根中找到。

堆的构造实现

private static final int DEFAULT_CAPACITY=10;//定义堆的大小
private int currentSize;//当前实际堆的大小
private T [] array;    //数组表示堆中元素

 public BinaryHeap(int capacity) {//初始化堆数组
         currentSize=0;
         array=(T[])new Comparable[capacity+1];
 }
 public BinaryHeap(T[] items) {
         currentSize=items.length;
         array=(T[])new Comparable[(currentSize+2)*11/10];

         int i=1;
         for(T item:items)
             array[i++]=item;//堆数组赋值
         buildHeap();
 }

private void buildHeap() {
    for(int i=currentSize/2;i>0;i--)//逐层下滤
        percolateDown(i);
}

注意！用数组实现堆时，元素的下标是从1开始，不是从0开始。原因是因为当插入的元素是比堆顶还小的元素时，我们不需要对堆做任何操作即可把堆冒出。

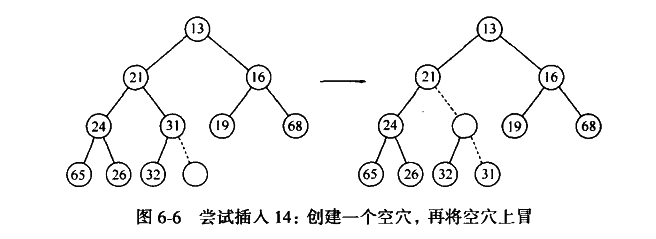
元素插入

 public void insert(T x) {
         if(currentSize==array.length-1)
             enlargeArray(array.length*2+1);//堆扩容
         int hole=++currentSize;    //空穴表示的数组下标
         /*
          * hole/2是当前空穴的父节点的数组下标，如果x比父节点的元素小，则父节点元素下沉，空穴上冒
          * */
         for(array[0]=x;x.compareTo(array[hole/2])<0;hole/=2)
             array[hole]=array[hole/2];    //元素交换
         array[hole]=x;
 }

删除最小元

　删除最小元基本的思想是将最小元置为空穴，再将堆的最后一个元素放入其中，则此时的堆是不合法的，我们需要做的就是将此时的堆顶元素下沉到合适的位置。

 public T deleteMin() throws Exception {
         if(isEmpty())
             throw new Exception();
         T minItem=findMin();//获取最小元
         array[1]=array[currentSize--];//取出最后一个元素
         percolateDown(1);//元素下滤
         return minItem;
 }

 private void percolateDown(int hole) {//下滤元素
         int child;
         T tmp=array[hole];
         for(;hole*2<=currentSize;hole=child) {
             child=hole*2;//孩子节点的下标
             if(child!=currentSize&&
                     array[child+1].compareTo(array[child])<0)//找出较小的孩子节点
                 child++;
             if(array[child].compareTo(tmp)<0)//逐层下滤
                 array[hole]=array[child];//元素替换
             else
                 break;
         }
         array[hole]=tmp;
 }

全部代码实现（数据结构与算法分析中的demo）

 // BinaryHeap class
 //
 // CONSTRUCTION: with optional capacity (that defaults to 100)
 //               or an array containing initial items
 //
 // ******************PUBLIC OPERATIONS*********************
 // void insert( x )       --> Insert x
 // Comparable deleteMin( )--> Return and remove smallest item
 // Comparable findMin( )  --> Return smallest item
 // boolean isEmpty( )     --> Return true if empty; else false
 // void makeEmpty( )      --> Remove all items
 // ******************ERRORS********************************
 // Throws UnderflowException as appropriate

 /**
  * Implements a binary heap.
  * Note that all "matching" is based on the compareTo method.
  * @author Mark Allen Weiss
  */
 public class BinaryHeap<AnyType extends Comparable<? super AnyType>>
 {
     /**
      * Construct the binary heap.
      */
     public BinaryHeap( )
     {
         this( DEFAULT_CAPACITY );
     }

     /**
      * Construct the binary heap.
      * @param capacity the capacity of the binary heap.
      */
     public BinaryHeap( int capacity )
     {
         currentSize = 0;
         array = (AnyType[]) new Comparable[ capacity + 1 ];
     }

     /**
      * Construct the binary heap given an array of items.
      */
     public BinaryHeap( AnyType [ ] items )
     {
             currentSize = items.length;
             array = (AnyType[]) new Comparable[ ( currentSize + 2 ) * 11 / 10 ];

             int i = 1;
             for( AnyType item : items )
                 array[ i++ ] = item;
             buildHeap( );
     }

     /**
      * Insert into the priority queue, maintaining heap order.
      * Duplicates are allowed.
      * @param x the item to insert.
      */
     public void insert( AnyType x )
     {
         if( currentSize == array.length - 1 )
             enlargeArray( array.length * 2 + 1 );

             // Percolate up
         int hole = ++currentSize;
         for( array[ 0 ] = x; x.compareTo( array[ hole / 2 ] ) < 0; hole /= 2 )
             array[ hole ] = array[ hole / 2 ];
         array[ hole ] = x;
     }

     private void enlargeArray( int newSize )
     {
             AnyType [] old = array;
             array = (AnyType []) new Comparable[ newSize ];
             for( int i = 0; i < old.length; i++ )
                 array[ i ] = old[ i ];
     }

     /**
      * Find the smallest item in the priority queue.
      * @return the smallest item, or throw an UnderflowException if empty.
      */
     public AnyType findMin( )
     {
         if( isEmpty( ) )
             throw new UnderflowException( );
         return array[ 1 ];
     }

     /**
      * Remove the smallest item from the priority queue.
      * @return the smallest item, or throw an UnderflowException if empty.
      */
     public AnyType deleteMin( )
     {
         if( isEmpty( ) )
             throw new UnderflowException( );

         AnyType minItem = findMin( );
         array[ 1 ] = array[ currentSize-- ];
         percolateDown( 1 );

         return minItem;
     }

     /**
      * Establish heap order property from an arbitrary
      * arrangement of items. Runs in linear time.
      */
     private void buildHeap( )
     {
         for( int i = currentSize / 2; i > 0; i-- )
             percolateDown( i );
     }

     /**
      * Test if the priority queue is logically empty.
      * @return true if empty, false otherwise.
      */
     public boolean isEmpty( )
     {
         return currentSize == 0;
     }

     /**
      * Make the priority queue logically empty.
      */
     public void makeEmpty( )
     {
         currentSize = 0;
     }

     private static final int DEFAULT_CAPACITY = 10;

     private int currentSize;      // Number of elements in heap
     private AnyType [ ] array; // The heap array

     /**
      * Internal method to percolate down in the heap.
      * @param hole the index at which the percolate begins.
      */
     private void percolateDown( int hole )
     {
         int child;
         AnyType tmp = array[ hole ];

         for( ; hole * 2 <= currentSize; hole = child )
         {
             child = hole * 2;
             if( child != currentSize &&
                     array[ child + 1 ].compareTo( array[ child ] ) < 0 )
                 child++;
             if( array[ child ].compareTo( tmp ) < 0 )
                 array[ hole ] = array[ child ];
             else
                 break;
         }
         array[ hole ] = tmp;
     }

         // Test program
     public static void main( String [ ] args )
     {
         int numItems = 10000;
         BinaryHeap<Integer> h = new BinaryHeap<>( );
         int i = 37;

         for( i = 37; i != 0; i = ( i + 37 ) % numItems )
             h.insert( i );
         for( i = 1; i < numItems; i++ )
             if( h.deleteMin( ) != i )
                 System.out.println( "Oops! " + i );
     }
 }