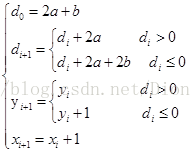OpenGL1.0 线段
OpenGL1.0线段
DionysosLai2014-06-16
本篇作为我学习Opengl第一篇文档。希望自己能在图形学路上走得远一点,达到可以渲染游戏画质目的,现阶段是Box2D对物理世界模拟非常好。但自己无法做到材质渲染非常好,致使很多效果差强人意。
谈到,画线。相信非常多游戏引擎都非常好的完美支持了,仅仅须要给出起点和终点,就行非常好的帮你实现画线问题。
我们今天来分析底层是怎样实现的。(ps:知识是网上视频学到,这里仅仅是起到一个学习记录作用。顺便分享出来,没有盗取他人成果意思)。这里先做两点如果:1. 起始点x0 < x1; 2. 线段斜率0~1之间。
1. 直线方程方法
基本思想:利用直线方程几何方程y=mx+b,确定路径上的像素点位置。
方法:逐点添加x的值,求出相应y的值,在进行取整运算;
主要运算:乘法+加法+取整---->这些是浮点运算
2. DDA(Digital DifferentialAnalyzer,数字差分分析法)方法
基本思想:y(i+1) = m(x(i+1))+b=mxi+m+b=yi+m;
方法:就是每次都要获取前面的y值
主要运算:加法+取整---->取整是浮点运算
代码例如以下:
void lineDDA(int x0, int y0, int x1, int y1)
{
/* x0 <= x1, 0 < m < 1*/
int x;
float m, dx, dy, y;
dx = x1 - x0;
dy = y1 - y0;
m = dy / dx;
y = y0;
for(x = 0; x <= x1, ++x)
{
int iy = (int)(y + 0.5);
SetPixel(x, iy); ///< 画点
y = y + m;
}
}3. 中点运算方法
目标:消除DDA中的浮点运算。浮点取整运算。不利于硬件实现。
直线的一般方程:F(x,y) = ax + by + c = 0; 当中 a=y0-y1=-dy;b=x1-x0=dx; c=x0y1-x1y0
方法:依据所取点间的中点(xi+1,yi+0.5)在直线的位置
依据中点坐标(xi+1,yi+0.5)。构造方程d=F(M)=F(xi+1,yi+0.5)的值,依据d的值,推断M在线段位置:d>=0,中点M在线段上方,取E, d<0, 中点在线段下方,取NE, 如图所看到的:
watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvRGlvbnlzb3NfbGFp/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center" alt="" />
怎样推断下一个像素呢
如果当前像素点(x+1, y+0.5)的d值,參考上面计算:
1).d>=0, 则取像素点E,那么下一个像素点的d值为:
d=F(xi+2,yi+0.5)=a(xi+2)+b(yi+0.5)+c=d+a;----->明显可以看到d的增量为a;
2).d<0, 则取像素点NE,那么下一个像素点的d值为:
d=F(xi+2,yi+1.5)=a(xi+2)+b(yi+1.5)+c=d+a+b,------>明显d的增量为a+b;
既然d的增量公式知道了,以下就是要知道d的初始值。依据构造方程d0=F(x0+1,y0+0.5)=F(x0,y0)+a+0.5b=a+0.5b; 在这里d0的运算结果有存在个0.5,即除法运算。也就是浮点运算,因为我们并不须要d的值。关系的是d与0的大小关系,因此,两边同一时候乘以2,消除浮点运算。
OK,至此我们可以得到以下的递推关系:
那么。终于结果就是例如以下所看到的:
主要运算:加法-->没有浮点运算
代码例如以下:
void lineMidPoint(int x0, int y0, int x1, int y1)
{
/* x0 <= x1, 0 < m < 1*/
int a, b, d1, d2, d, x, y;
a = y0 - y1;
b = x1 - x0;
d = a + a + b;
d1 = a + a;
d2 = (a+b) + (a+b);
x = x0;
y = y0;
SetPixel(x,y); ///< 画点
while(x < x1)
{
if(d<0)
{
++y;
d += d2;
}
else
d += d1;
x++;
SetPixel(x,y); ///< 画点
}
}Ok。这就是我今天所学的。快一点了,该睡觉。明天生活更美好。
OpenGL1.0 线段的更多相关文章
- HDU 1394 Minimum Inversion Number(最小逆序数/暴力 线段树 树状数组 归并排序)
题目链接: 传送门 Minimum Inversion Number Time Limit: 1000MS Memory Limit: 32768 K Description The inve ...
- HDU 5023 A Corrupt Mayor's Performance Art (据说是线段树)
题意:给定一个1-n的墙,然后有两种操作,一种是P l ,r, a 把l-r的墙都染成a这种颜色,另一种是 Q l, r 表示,输出 l-r 区间内的颜色. 析:应该是一个线段树+状态压缩,但是我用s ...
- OpenGL2.0及以上版本中glm,glut,glew,glfw,mesa等部件的关系
OpenGL2.0及以上版本中gl,glut,glew,glfw,mesa等部件的关系 一.OpenGL OpenGL函数库相关的API有核心库(gl),实用库(glu),辅助库(aux).实用工具库 ...
- 【POJ】2828 Buy Tickets(线段树+特殊的技巧/splay)
http://poj.org/problem?id=2828 一开始敲了个splay,直接模拟. tle了.. 常数太大.. 好吧,说是用线段树.. 而且思想很拽.. (貌似很久以前写过貌似的,,) ...
- HDU 1394 Minimum Inversion Number(线段树/树状数组求逆序数)
Minimum Inversion Number Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java ...
- NBOJv2 1050 Just Go(线段树/树状数组区间更新单点查询)
Problem 1050: Just Go Time Limits: 3000 MS Memory Limits: 65536 KB 64-bit interger IO format: % ...
- Stars(树状数组或线段树)
Stars Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 37323 Accepted: 16278 Description A ...
- [BZOJ 1901] Dynamic Rankings 【树状数组套线段树 || 线段树套线段树】
题目链接:BZOJ - 1901 题目分析 树状数组套线段树或线段树套线段树都可以解决这道题. 第一层是区间,第二层是权值. 空间复杂度和时间复杂度均为 O(n log^2 n). 线段树比树状数组麻 ...
- poj 2481 Cows(数状数组 或 线段树)
题意:对于两个区间,[si,ei] 和 [sj,ej],若 si <= sj and ei >= ej and ei - si > ej - sj 则说明区间 [si,ei] 比 [ ...
随机推荐
- Unity3D 5.0版本+注册工具分享
Unity3D引擎5.0正式版本发布也有一段时间了.笔者今天下载了新版本顺便分享一下资源. 主要有两个资源,一个是5.0f4的官方客户端,另外一个是vs的调试插件.有需要的盆友就拿去.都在下面的连接地 ...
- java生成webservice
使用Eclipse生成一个WebService应用 1.创建一个Dynamic web project 2.创建一个对外提供服务的类.比如: package com.guorui.services; ...
- 74HC164dD驱动LED
驱动要点: 1.上升沿写入串行数据: CLK=0; DAT=num&0x01; CLK=1; 2.写入数据的数码管编码(指代码中的 tab[]) 串行数据是FIFO先进先出,也就是先写高位,移 ...
- jQuery补充,模拟图片放大镜
jQuery补充,模拟图片放大镜 html <!DOCTYPE html> <html lang="en"> <head> <meta c ...
- Codeforces Round #266 (Div. 2)
http://codeforces.com/contest/466 噗,b没写出来啊.a写完后过了40分钟了啊,罚时4次啊!果然太弱 总结: a题看错题,没有考虑m>=n其实也是可行的,导致调了 ...
- debugging openstack with pdb
在要开始debug的地方导入pdb: class KeypairAPI(base.Base): """Sub-set of the Compute Manager API ...
- mysql根据查询结果,创建表
create table copy_materials_details (SELECT * FROM `materials_details`);
- 收藏几个支持中文的PHP字符串截取函数
字符串截取是一个非常常见的编程任务,而往往带中文的字符串截取会经常用到.虽然不难,但是自己写函数实现又耗费时间,这里介绍一个比较好用的字符串截取函数,能够胜任基本的需求了. <?php func ...
- 我学cocos2d-x (一) 游戏基本概念:坐标系与Anchor Point
坐标系: 游戏开发中.全部物体都有自己的位置,而我们须要一个參考系来描写叙述物体的位置.使用cocos2d-x开发的时候.有几个比較重要坐标系须要掌握:屏幕坐标系和Cocos2d坐标系 屏幕坐标系: ...
- typescript 实现函数重载
class Demo { // #region 声明 log() : void; log(arg1: string): void; log(arg1: number, arg2: string): v ...