hdu 1174:爆头（计算几何，三维叉积求点到线的距离）

爆头

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 1447    Accepted Submission(s): 601

Problem Description

gameboy是一个CS高手，他最喜欢的就是扮演警察，手持M4爆土匪的头。也许这里有人没玩过CS，有必要介绍一下“爆头”这个术语：所谓爆头，就是子弹直接命中对方的头部，以秒杀敌人。

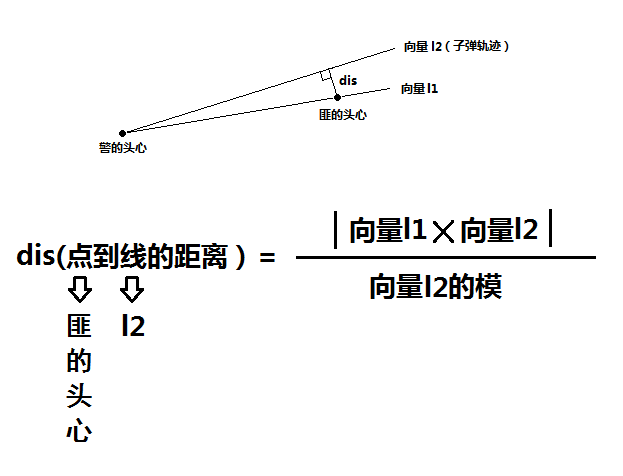
现在用一个三维的直角坐标系来描述游戏中的三维空间（水平面为xoy平面，z轴正方向是上方）。假设游戏中角色的头是一个标准的球。告诉你土匪的身高，头部半径，所站位置的坐标；gameboy所控警察的身高，头部半径，所站位置的坐标，以及枪头所指方向的单位向量。gameboy所控警察所握的是M4，抢瞄准时枪膛中的子弹跟视线基本同线，我们忽略它们的距离，就当成同线。由于土匪手持AK47,所以他是很嚣张地正立着。而警察手持M4，正在瞄准，由于瞄准时身体微弯，视线从头心出发，他头部的实际高度比正立时低10%。

你的任务就是，计算gameboy在这一刻扣下扳机，能否爆土匪的头。注意：这里忽略子弹的直径和重力作用，也就是说子弹是无限小的，弹道是一条笔直的射线，警察与土匪间没有障碍物。并且只要子弹擦到头部，哪怕是边缘，也算爆头。

 

Input

测试数据的第一行有一个正整数T，表示有T组测试数据。每组数据的第一行有五个实数，h1,r1,x1,y1,z1，分别表示土匪的身高，头部半径以及所站的位置。第二行有八个实数，h2,r2,x2,y2,z2,x3,y3,z3，分别表示警察的身高，头部半径，所站位置，以及枪头所指方向的方向向量。

 

Output

每一组输入数据对应一行输出。如果能爆土匪的头，输出"YES",否则输出"NO"。

 

Sample Input

2
1.62 0.1 10.0 10.0 10.0
1.80 0.09 0.0 0.0 0.0 1.0 1.0 1.0
1.62 0.1 0.0 0.0 0.0
1.80 0.09 10.0 10.0 10.0 -1.0 -1.0 -1.0

 

Sample Output

YES
YES

 

Author

lwg

 

Recommend

We have carefully selected several similar problems for you:  1172 1176 1107 1246 1247 

---

 

　　计算几何：三维向量的叉积求点到线的距离。

　　三维向量的叉积可以求点到线的距离，对这道题来说就是求匪的头心到子弹射出形成的射线间的距离（dis）。那么可以用如下公式来求。

　　

 　　

　　三维向量的叉积模板：

 struct Vector3{    //方向向量
     double x,y,z;
 };
 double xmulti3(Vector3 v1,Vector3 v2)    //三维向量的叉积
 {
     double x1 = v1.x;
     double y1 = v1.y;
     double z1 = v1.z;
     double x2 = v2.x;
     double y2 = v2.y;
     double z2 = v2.z;
     double x = y1*z2 - z1*y2;
     double y = z1*x2 - x1*z2;
     double z = x1*y2 - y1*x2;
     return sqrt(x*x+y*y+z*z);
 }

　　参考链接：

　　ACM HDU 1174 爆头（数学题，求空间点到直线的距离，用叉积）

　　http://blog.sina.com.cn/s/blog_70743a560100lneu.html

　　

　　本题代码：

 #include <iostream>
 #include <cmath>
 using namespace std;
 struct Vector3{    //方向向量
     double x,y,z;
 };
 double xmulti3(Vector3 v1,Vector3 v2)    //三维向量的叉积
 {
     double x1 = v1.x;
     double y1 = v1.y;
     double z1 = v1.z;
     double x2 = v2.x;
     double y2 = v2.y;
     double z2 = v2.z;
     double x = y1*z2 - z1*y2;
     double y = z1*x2 - x1*z2;
     double z = x1*y2 - y1*x2;
     return sqrt(x*x+y*y+z*z);
 }
 int main()
 {
     double h1,r1,x1,y1,z1;
     double h2,r2,x2,y2,z2,x3,y3,z3;
     int T;
     cin>>T;
     while(T--){
         cin>>h1>>r1>>x1>>y1>>z1;
         cin>>h2>>r2>>x2>>y2>>z2>>x3>>y3>>z3;
         Vector3 v1,v2;
         //确定警头心到匪头心的射线
         v1.x = x1 - x2;
         v1.y = y1 - y2;
         v1.z = z1 + h1 -r1 - ( h2*0.9 + z2 -r2);
         //确定子弹射线
         v2.x = x3;
         v2.y = y3;
         v2.z = z3;
         //求匪的头心到射线的距离
         double dis = fabs(xmulti3(v1,v2))/sqrt(x3*x3+y3*y3+z3*z3);
         //判断能否爆头
         if(dis <= r1)
             cout<<"YES"<<endl;
         else
             cout<<"NO"<<endl;
     }
     return ;
 }

Freecode : www.cnblogs.com/yym2013