寻找最大(小)的K个数

　　<<编程之美>>一书中提到了寻找最大的K个数的问题，问题可以简单描述为：在长度为N的数组中，寻找第K(K<N)个最大的数。问题的解法涉及到了很多排序算法，对我们理解和运用排序算法有较大帮助。

　　1.解决方案

　　解决思路一：我们首先可以想到的方法，先对数据进行排序，然后选择K个最大的值，算法时间复杂度O(N*logN) + O(K) = O(N*logN)。

解决思路二：注意到题目要求造成K个最大的数，并没有要求这个K个最大的数是否有序。联想到快速排序算法，快速排序算法每一步可以讲数组分词两个部分，其中，一个部分的所有元素均要小于另一部分的所有元素。我们可以利用快速排序算法思想，分割数据，产生K个最大的原始，算法的步骤如下：两个部分

1）随机选择pivot元素，将数组分成S_a与S_b两个部分，

2）若S_b长度大于等于K，则返回S_b中寻找第K的最大元素；

　  3）若S_b长度小于等于K，则返回S_a中第K-|S_b|个最大元素

算法平均时间复杂度O(N*logK)。

　　解决思路三：在N个元素中找出K个最大的元素，本质上与寻找K个最大的元素中最小的那个，我们假设这个元素是Vk，N个元素中最大的是Vmax，最小的元素是是Vmin。那么Vk，必然在[Vmin，Vmax]之间，因此我们可以使用二分查找排序的方法在[Vmin，Vmax]之间找出这个原则Vk。

　　解决思路四：上面的三种解决方案，都需要将N个元素加载到内存，但如果N是一个非常大的值，比如超过4G空间，现有的内存空间加载这N个元素失败，造成三种算法失效。对于这个问题，我们可以考虑采用“在线更新”策略：维持K个元素，对于一个新的元素，如果比K个元素中最小元素小，则不更新当前的K个元素；如果新的元素要比K个元素中最小元素大，则更新这个K个原则。于是乎一种优美更新排序方法，堆排序算法，进入了我们的视野。

　　解决思路五：直方图法，假设存在这样的一个直方图，该直方图的横坐标是序列中出现的元素，而纵坐标则是序列中改元素出现的次数。当我需要K个最大的元素，只需要沿着横坐标反方向，累加相应纵坐标相应的值，直到k为止。这个方法依赖于哈希结构。算法的时间复杂度O(N)，然而算法需要额外的存储结构哈希表。

　　2.基础算法实现

　　上述解决方案中，依赖与基础算法：快速排序，堆排序，因此，我们首先实现这三个基础算法。

• 　　堆排序算法实现：

　　堆排序(heap sort)算法是一种非常优良的算法，特别在当今大数据的时代，亦更能体现其价值，奥地利符号计算研究所的Christoph Koutschan博士在自己的页面上发布一篇文章，选出了计算机科学中最重要的32个算法，快速排序位列其中。堆排序算法的平均时间复杂度O(N*logN)。

　　首先简单回顾一下堆排序算法，堆排序算法依赖与二叉树定义的数据结构，它定义父节点的值均大于子节点的值。堆属于完全二叉树，可以将堆简单的映射到向量存储结构中，具有高效的实现效率，假设存储节点的下标从1开始，父节点下标记为i，则左子节点下标2*i，右子节点下标2*i + 1。此外涉及堆的操作包括：堆的构建、入堆，出堆已经堆排序。

　　算法实现上，我们检查C++SLT中是否有heap数据结构，如果有，就可以直接拿过来用。可惜的是，STL中并没有把heap单独作为一种容器，而是把它作为其他容器的底层容器(如Priority Queue)，但STL在泛型算法提高了构造heap堆的接口，我们可以依托vector与相关堆的算法，实现堆排序功能。

//STL heap implement, main.cpp

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int _tmain(int argc,_TCHAR* argv[])
{

  int myints[] = {, , , , };
  vector<int> v(myints, myints+);

  make_heap (v.begin(),v.end());             //构建堆
  cout << "initial max heap   : " << v.front() << '\n';

  pop_heap (v.begin(), v.end());             //出堆，返回最大的元素，STL并没有删除该值，而是放在vector尾端
  v.pop_back();
  cout << "max heap after pop : " << v.front() << '\n';

  v.push_back();                           //入堆，调整堆结构
  push_heap (v.begin(),v.end());
  cout << "max heap after push: " << v.front() << '\n';

  sort_heap (v.begin(),v.end());              //强制排序

  cout << "final sorted range :";
  for (unsigned i=; i<v.size(); i++)
    cout << ' ' << v[i];

  cout << '\n';

  system("pause");
  return ;

}

　例子源于这里略有改动，以上是STL“算法”的堆实现，用起来并不是很方便，因此，我们尝试直接实现堆数据结构。

// heap.h
#ifndef HEAP_H
#define HEAP_H

#include <vector>
#include <iostream>
#include <functional>
#include <climits>

using namespace std;

const int start_index = ;      //容器中堆元素起始索引

template <typename T, typename Compare = less<T> >
class Heap
{
public:
    Heap();
    void InitHeap(T *data,const int n);   //初始化操作
    void MakeHeap();                      //建堆
    void PushHeap(T elem);                //向堆中插入元素
    void PopHeap();                       //堆顶元素出堆
    vector<T> SortHeap();
    T Top();                              //从堆中取出堆顶的元素
    bool IsEmpty();                       //判读堆是否为空
    size_t size() const;
    void PrintHeap() const;

private:
    void adjustHeap(int childTree, T adjustValue);  //调整子树
    void percolateUp(int holeIndex, T adjustValue); //上溯操作

private:
    vector<T> heapDataVec;                           //存放元素的容器
    int heapSize;                                   //堆中元素个数
    Compare comp;                                    //比较规则
};

#endif

//heap.cpp

#include "heap.h"

using namespace std;

template <typename T, typename Compare>
Heap<T,Compare>::Heap():heapSize()
{
    heapDataVec.push_back(INT_MAX);
}

template <typename T, typename Compare>
void Heap<T,Compare>::InitHeap(T *data, const int n)
{
    for (int i = ;i < n;++i)
    {
        heapDataVec.push_back(*(data + i));
        ++heapSize;
    }
}

template <typename T, typename Compare>
size_t Heap<T,Compare>::size() const
{
    return heapSize;
}

template <typename T, typename Compare>
T Heap<T, Compare>::Top()
{
    return heapDataVec[start_index];
}

template<typename T, typename Compare>
bool Heap<T, Compare>::IsEmpty()
{
    return heapSize == ;
}

template<typename T, typename Compare>
void Heap<T, Compare>::PrintHeap() const
{
    for (int i = ; i <= heapSize; i++)
        cout<< heapDataVec[i]<<" ";
    cout<<endl;
}

template <typename T, typename Compare>
void Heap<T, Compare>::MakeHeap()
{
    //建堆：从叶节点开始调整不断的调整堆
    if (heapSize < )
        return;

    int parent = heapSize / ;  //第一个需要调整的子树的根节点多，起始下标从1开始
    while()
    {
        adjustHeap(parent,heapDataVec[parent]);
        if (start_index == parent)
            return;

        --parent;
    }
}

template <typename T,typename Compare>
vector<T> Heap<T,Compare>::SortHeap()
{
    //堆排序：堆中所以元素出堆的过程

    while(!IsEmpty())
        PopHeap();

    return vector<T>(heapDataVec.begin() + , heapDataVec.end());
}

template <typename T, typename Compare>
void Heap<T,Compare>::PushHeap(T elem)
{
    //将新元素添加到vector底部，并执行一次上溯
    heapDataVec.push_back(elem);
    ++heapSize;
    percolateUp(heapSize,heapDataVec[heapSize]);//执行一次上溯操作，调整堆，以使其满足最大堆的性质
}

template <typename T, typename Compare>
void Heap<T,Compare>::PopHeap()
{
    //将堆顶的元素放在容器的最尾部，然后将尾部的原元素作为调整值，重新生成堆
    T adjustValue = heapDataVec[heapSize];
    heapDataVec[heapSize] = heapDataVec[start_index];
    --heapSize;
    adjustHeap(start_index,adjustValue);
}

template <typename T,typename Compare>
void Heap<T,Compare>::adjustHeap(int childTree,T adjustValue)
{
    //调整以childTree为根的子树为堆
    int holeIndex = childTree;
    int secondChid =  * holeIndex + ;                    //洞节点的右子节点（注意：起始索引从1开始）

    while(secondChid <= heapSize)
    {
        if (comp(heapDataVec[secondChid],heapDataVec[secondChid - ]))
        {
            --secondChid;
        }

        heapDataVec[holeIndex] = heapDataVec[secondChid]; //令较大值为洞值
        holeIndex = secondChid;                           //洞节点索引下移
        secondChid =  * secondChid + ;                  //重新计算洞节点右子节点
    }

    if (secondChid == heapSize + )                       //如果洞节点只有左子节点
    {
        heapDataVec[holeIndex] = heapDataVec[secondChid - ];
        holeIndex = secondChid - ;
    }

    heapDataVec[holeIndex] = adjustValue;  //将待调整值放入到叶子节点
    percolateUp(holeIndex,adjustValue);    //需要再执行一次上溯操作
}

template <typename T, typename Compare>
void Heap<T,Compare>::percolateUp(int holeIndex,T adjustValue)
{
    //上溯操作： 将新节点与其父节点进行比较，如果键值比其父节点大，就父子交换位置。
    //          直到不需要对换或直到根节点为止
    int parentIndex = holeIndex / ;
    while(holeIndex > start_index && comp(heapDataVec[parentIndex],adjustValue))
    {
        heapDataVec[holeIndex] = heapDataVec[parentIndex];
        holeIndex = parentIndex;
        parentIndex /= ;
    }
    heapDataVec[holeIndex] = adjustValue;
}

// main.cpp
#include "heap.h"
#include "heap.cpp"

#include <iostream>

using namespace  std;

int main()
{
    const int heap_size = ;
    int data[heap_size] = {,,,,};

    Heap<int> myHeap;
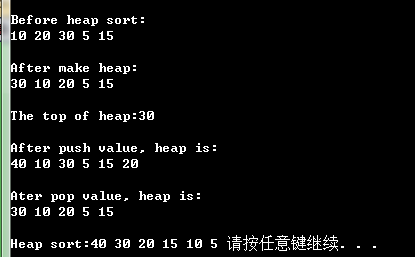
    myHeap.InitHeap(data, );

    cout<<"\nBefore heap sort:"<<endl;
    myHeap.PrintHeap();

    myHeap.MakeHeap();
    cout<<"\nAfter make heap:"<<endl;
    myHeap.PrintHeap();

    cout<<"\nThe top of heap:"<<myHeap.Top()<<endl;

    myHeap.PushHeap();
    cout<<"\nAfter push value, heap is:"<<endl;
    myHeap.PrintHeap();

    cout<<"\nAter pop value, heap is:"<<endl;
    myHeap.PopHeap();
    myHeap.PrintHeap();

    vector<int> sortedHeap = myHeap.SortHeap();
    cout<<"\nHeap sort:";
    for (vector<int>::reverse_iterator riter = sortedHeap.rbegin(); riter != sortedHeap.rend(); riter++)
        cout<<*riter<<" ";

    system("pause");
    return ;
}

程序的运行的程序的结果如下:

• 快速排序算法实现

　　快速排序算法在算法占有举足轻重的位置，在<<The Best of the 20th Century: Editors Name Top 10 Algorithms>>一文中，列举了20实际最伟大的算法，快速排序位列其中，很多人认为，快速排序算法是排序算法的首先，可惜的是最近列出的32个计算机的重要算法中，没有列出，不知为何。

　　快速排序算法属于典型的快速分治算法：将原问题划分成更小的子问题，其中，每个更小的子问题都有着与原问题相同的解形式。假设待排序的数组A[p...r]，快速排序算法的基本思路如下：

　　1）分解：将A[p...r]分解成两个部分A[p...q]与A[q+1, r]两个部分，其中A[p...q]中的元素均小于A[q+1, r]中的元素

　　2）子问题：两个子问题A[p...q-1]与A[q+1, r]的排序，与原问题形式相同，递归调用快速排序

　　3）解的合并：子问题排序是直接在A中就地排序，因此无须合并结果，直接返回A，得到排序结果

　　快速排序的实现版本有多种，主要的区别在于：1）起始轴元素的选择，国内教材倾向于选择序列的第一个元素，而<<算法导论>>选择序列的最后一个元素；2）分解问题时，切分序列所采用的遍历方法不同，有的倾向于双向的遍历方法(严版数据结构采用的方法)，有的则使用单向的遍历方法(<<算法导论>>）采用的方法。本文给出个人认为较为优雅的实现方法((严版数据结构采用的方法)。

#include <iostream>
#include <algorithm>
#include <functional>

using namespace std;

template<typename T, typename Compare>
int partition(T* array, int low, int high, Compare cmp)
{
　　//分解算法，返回轴元素的位置
    T privot_value = array[low];
    while (low < high)
    {
        while((low < high) && (cmp(privot_value, array[high]))) //从高向低寻找小于轴元素的元素
            --high;

        swap(array[low],array[high]);                           //算法执行第一次与轴元素交换，之后，与大于轴元素的元素交换           

        while ((low < high) && (cmp(array[low], privot_value))) //从低向高寻找大于轴元素的元素
            ++low;

        swap(array[low], array[high]);
    }
    array[low] = privot_value;
    return low;
}

template<typename T, typename Compare>
void quick_sort(T* array, int low, int high, Compare cmp = less<int>())
{
    int privot_loc = partition(array, low, high, cmp);      //问题分解
    partition(array, low, privot_loc - , cmp);             //低半部分子问题求解
    partition(array, privot_loc + , high, cmp);            //高半部分子问题求解

}

int main()
{
    const int array_size = ;
    int my_array[array_size] = {, , , , };

    cout<<"Befor sort："<<endl;
    for (int i = ; i != array_size; i++)
        cout<<my_array[i]<<" ";

    quick_sort(my_array, , array_size-, less<int>());
    cout<<"After sort："<<endl;
    for (int i = ; i != array_size; i++)
        cout<<my_array[i]<<" ";
　　cout<<endl;

    system("pause");
    return ;
}

　　

　　快速排序算法的性能与轴元素的选择十分相关，在最坏情况下算法的时间复杂度O(N²)，算法平均的时间复杂度0(N*logN)。一种简单产生轴元素方法即在序列随机产生轴元素，此外一些文献中会论述了如何产生轴元素，有兴趣的读者可以翻阅相关文献。

　　3.寻找最大(小)排序元素C++实现

　　在第一个部分提到的五种解决思路中，思路一，思路四直接利用第二部分的的基础算法可以实现，思路三实现较为简单，我们实现剩下的两种种方法。

　　思路二的C++实现：

template<typename T, typename Compare>
T quick_select(T* array, int low, int high, int k, Compare cmp = less<int>())
{
    int privot_loc = partition(array, low, high, cmp);
    int m = high - privot_loc + ;

    if (m == k)
    {
        //如果当前轴在序列中的位置(从高到低)与K相同，
        //则直接返回轴元素
        return array[privot_loc];
    }
    else if (m < k)
    {
        //如果当前轴在序列中的位置(从高到低)小于k，
        //则在序列的低半部分，寻找剩下的k-m个最大值
        return quick_select(array, low, privot_loc -  , k-m, cmp);

    }
    else
    {
        //如果当前轴在序列中的位置(从高到低)大于k，
        //则在序列的高半部分，寻找剩下的k个最大值
        return quick_select(array, privot_loc + , high, k, cmp);
    }

}

int main()
{
    const int array_size = ;
    int k =;
    int my_array[array_size] = {, , , , , , , , , };
    cout<<"Please enter the kth greater: ";
    cin>>k;

    int kth_value = quick_select(my_array, , array_size - , k, less<int>());
    cout<<"The kth greater value is "<<kth_value;
    system("pause");
    return ;
}

quick_select调用了在在第二部分实现的partition部分，quick_select实现也与第二部分的quick_sort十分相似，只是多了域范围判断。

　　思路五的C++实现：

#include <iostream>
#include <algorithm>
#include <climits>

using namespace std;

int select_kth_max(int* array, int array_size, int k)
{
    int* p_max = max_element(array, array+array_size);
    int* hash_tabel = new int[*p_max];
    memset(hash_tabel,  , sizeof(int) * (*p_max));
    int kth_value = INT_MIN;

    for (int i = ; i != array_size; i++)
    {
        hash_tabel[array[i]]++;
    }

    int acc_num = ;
    for (int i = (*p_max) -; i >=; i--)
    {
        acc_num += hash_tabel[i];
        if (acc_num >= k)
        {
            kth_value = i;
            break;
        }
    }

    return kth_value;

}

int main()
{
    const int array_size = ;
    int my_array[array_size] = {, , , , , , , , , };
    int k ;
    cout<<"Please enter the kth greater: ";
    cin>>k;

    int kth_value = select_kth_max(my_array, array_size, k);
    cout<<"The kth greater value is "<<kth_value;

    system("pause");
    return ;
}

　　

　　4.参考文献

　　书籍：<<编程之美>>、<<算法导论>>、<<数据结构(c语言版)>>(严蔚敏)

　　网上资源： 编程艺术总结，http://blog.csdn.net/v_july_v/article/details/6543438

　　　　　　　 C++参考网站，http://www.cplusplus.com/reference/algorithm/make_heap/

C++堆实现，http://blog.csdn.net/xiajun07061225/article/details/8553808

ps：在算法实现上，使用了C++template技术，使用template遇到了一些小问题：

1）vs编译器，不支持模块头文件与实现文件的分离，否则会报Link Erro错误，解决方法有两种：

　　　　　　（1）模板的实现文件与头文件合在一起；

　　　　　　（2）仍然分离模板的实现文件与头文件，但在包含模板头文件的同时也包括实现文件。

　　　　2）C++类模板支持省略参数，但是C++模板函数并不支持默认参数（有点奇怪~）。