浅层神经网络 反向传播推导：MSE softmax

基础：逻辑回归

Logistic 回归模型的参数估计为什么不能采用最小二乘法？

logistic回归模型的参数估计问题不能“方便地”定义“误差”或者“残差”。

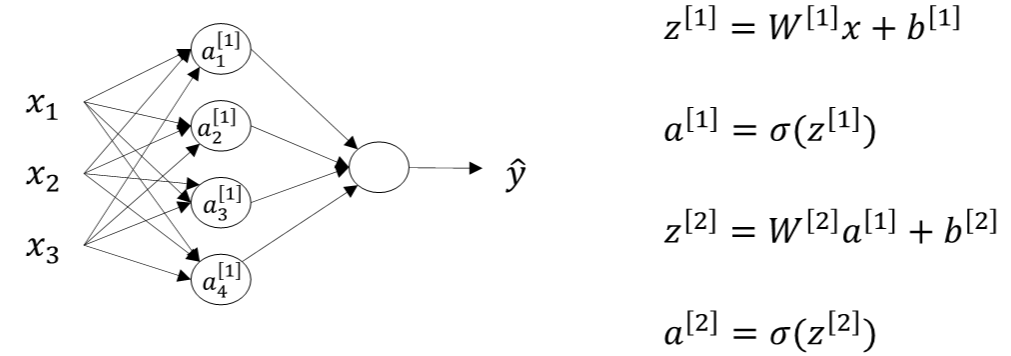
对单个样本：

第i层的权重W^[i]维度的行等于i层神经元的个数，列等于i-1层神经元的个数；第i层常数项b[i]b[i]维度的行等于i层神经元的个数，列始终为1。

对m个样本,用for循环不如用矩阵快，输入矩阵X的维度为（n_x,m），n_x是输入层特征数目。

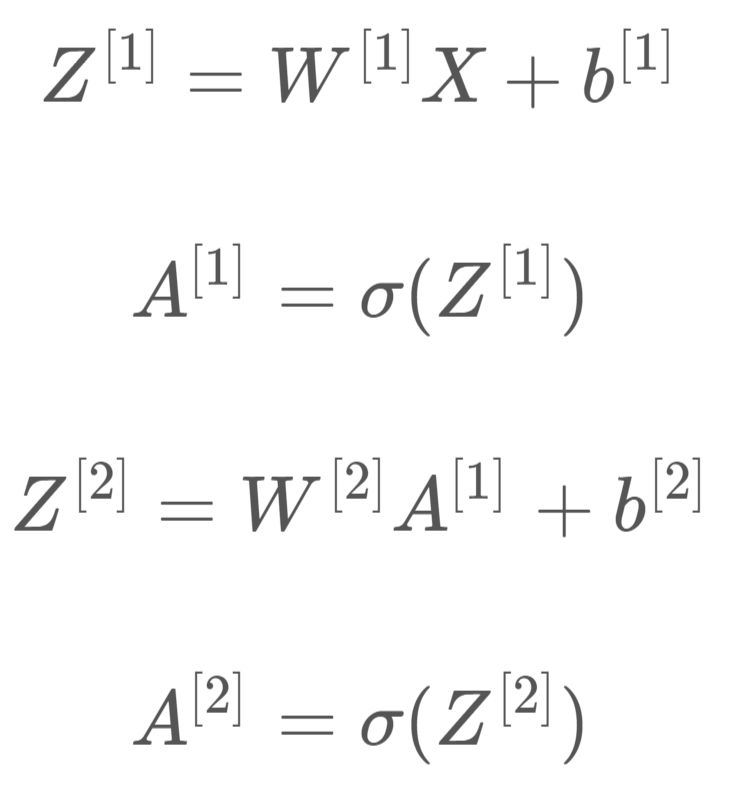
其中，Z^[1]的维度是（4,m），4是隐藏层神经元的个数；A^[1]的维度与Z^[1]相同；Z^[2]和A^[2]的维度均为（1,m）。行表示神经元个数，列表示样本数目m。

一文弄懂神经网络中的反向传播法——BackPropagation

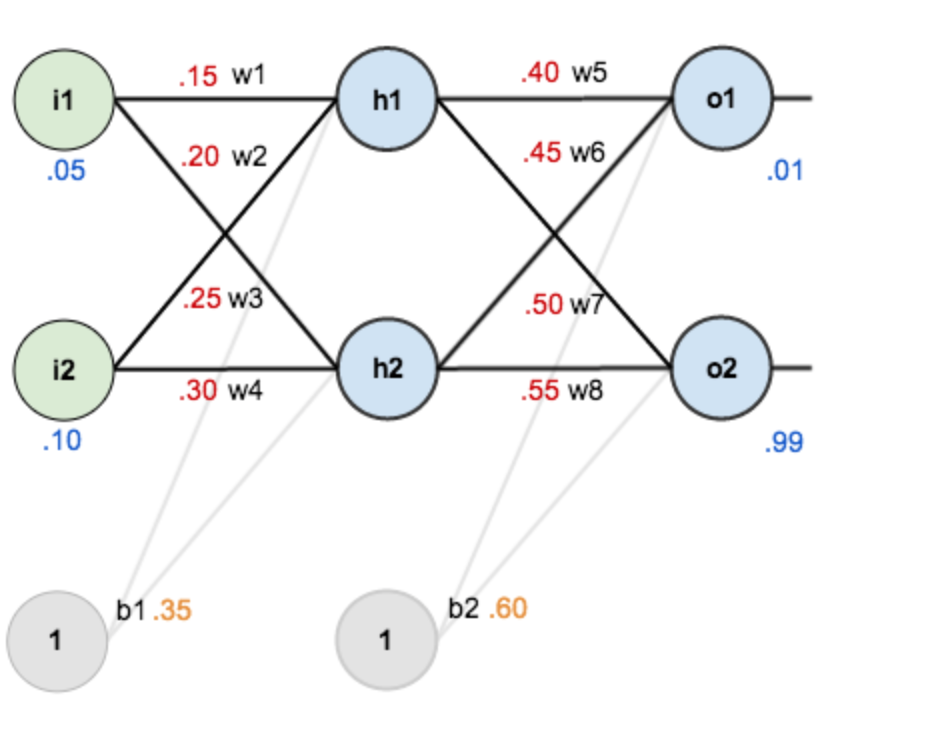
反向传播推导

输出层---->隐含层

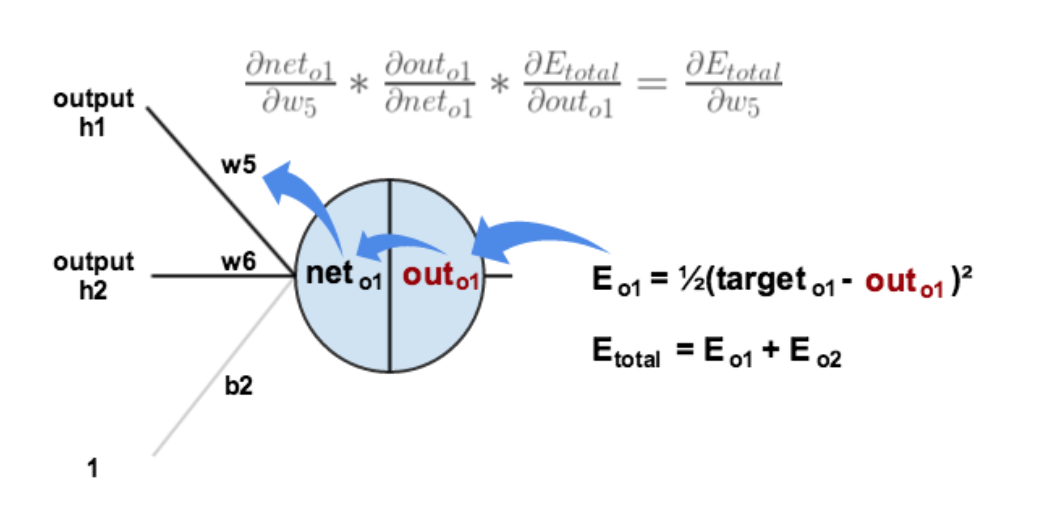
以w5为例，更新的是权值：

1.计算总误差

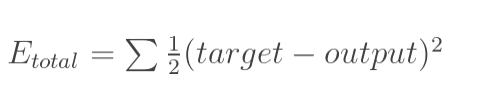
分别计算o1和o2的误差，总误差为两者之和

2.链式法则

计算：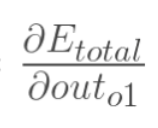

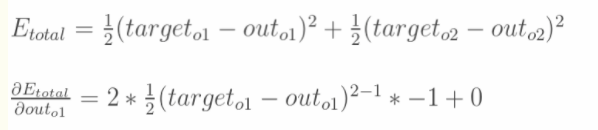
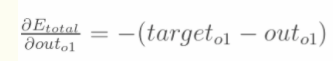
计算：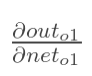

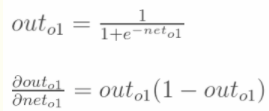
计算：

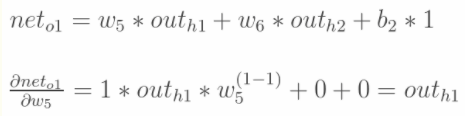
最后三者相乘：

更新w5的值：

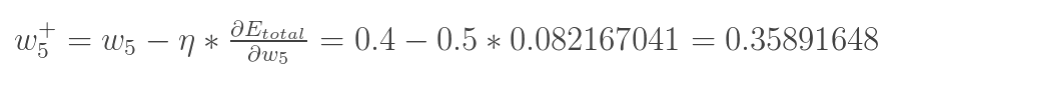
隐含层---->隐含层

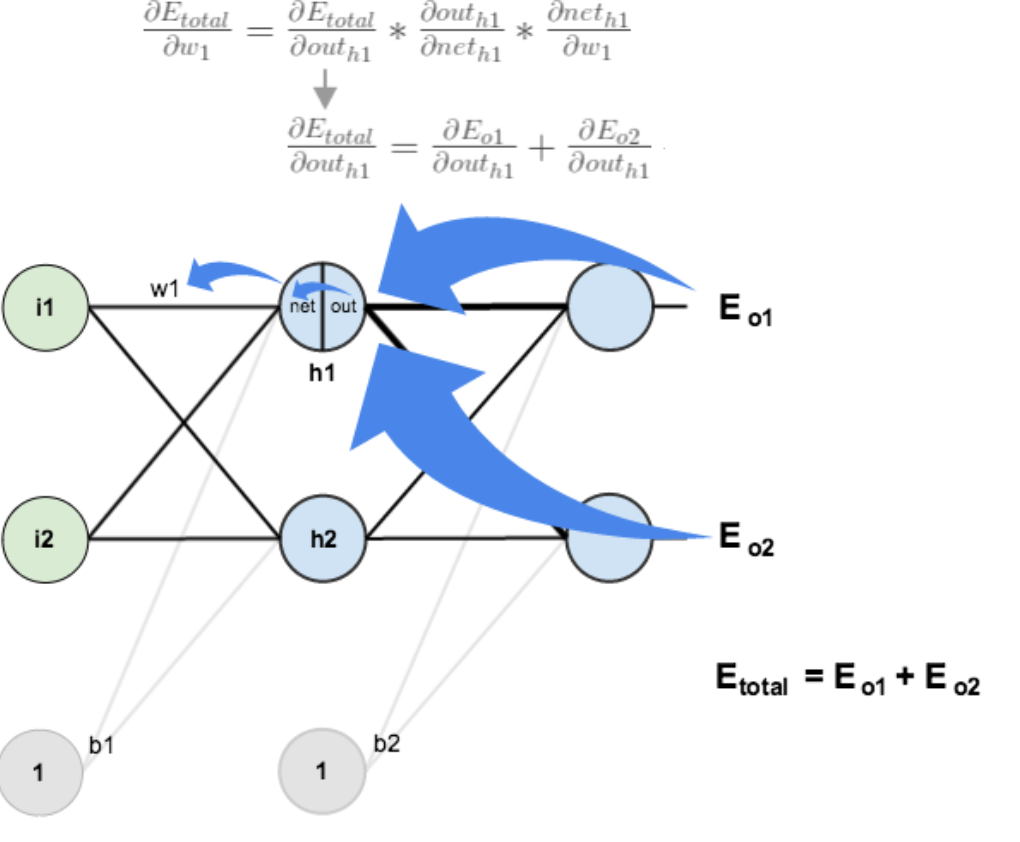
方法其实与上面说的差不多，但是有个地方需要变一下，在上文计算总误差对w5的偏导时，是从out(o1)---->net(o1)---->w5,但是在隐含层之间的权值更新时，是out(h1)---->net(h1)---->w1,而out(h1)会接受E(o1)和E(o2)两个地方传来的误差，所以这个地方两个都要计算。

先计算：***************************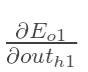

因为在正向传播中E_o1：

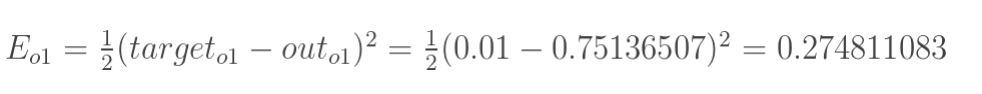
out_o1：

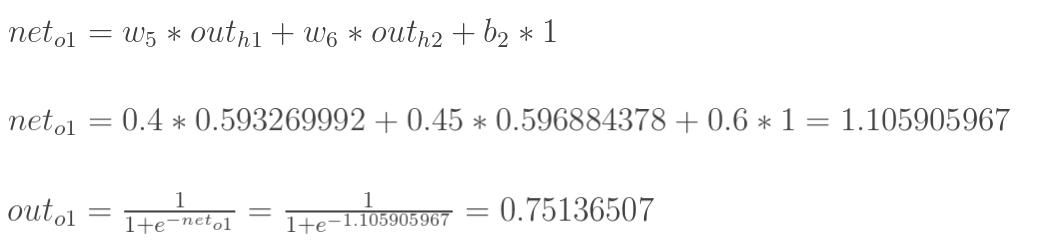
带入的话就是对net_o1求导，所以：

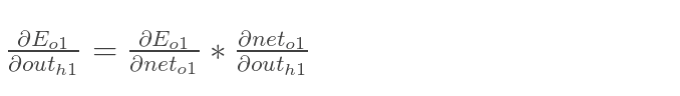
为了简化公式，用sigma(h1)表示隐含层单元h1的误差：

最后，更新w1的权值：

softmax反向传播

手打例子一步一步带你看懂softmax函数以及相关求导过程

交叉熵函数形式如下：

其中y代表我们的真实值，a代表我们softmax求出的值。i代表的是输出结点的标号

在真实中，如果只预测一个结果，那么在目标中只有一个yi结点的值为1，哎呀，这太好了，除了一个为1，其它都是0，那么所谓的求和符合，就是一个幌子，我可以去掉啦！

那么Loss就变成了Loss = -yjlnaj(yj,aj的j均为下标，公式不好打),累和已经去掉了，太好了。现在我们要开始求导数了！

我们在整理一下上面公式，为了更加明白的看出相关变量的关系：

其中yj=1,,那么形式变为  Loss = -lnaj

这里分为俩种情况：

这里i是aj的softmax函数分子z的下标

 

j=i对应例子里就是如下图所示：

比如我选定了j为4，那么就是说我现在求导传到4结点这！

 

那么由上面求导结果再乘以交叉熵损失函数求导

Loss = -lnaj,它的导数为-1/aj,与上面的aj(1-aj)相乘为aj-1（形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果减1即可，后面还会举例子！）那么我们可以得到Loss对于4结点的偏导就求出了了（这里假定4是我们的预计输出）

第二种情况为：

这里对应我的例子图如下，我这时对的是j不等于i，往前传

那么由上面求导结果再乘以交叉熵损失函数求导

Loss = -lnaj,它的导数是-1/aj,与上面-ajai相乘为ai（形式非常简单，这说明我只要正向求一次得出结果，然后反向传梯度的时候，只需要将它结果保存即可，后续例子会讲到）

下面我举个例子来说明为什么计算会比较方便，给大家一个直观的理解

举个例子，通过若干层的计算，最后得到的某个训练样本的向量的分数是[ 2, 3, 4 ],

那么经过softmax函数作用后概率分别就是=[e^2/(e^2+e^3+e^4),e^3/(e^2+e^3+e^4),e^4/(e^2+e^3+e^4)] = [0.0903,0.2447,0.665],如果这个样本正确的分类是第二个的话，那么计算出来的偏导就是[0.0903,0.2447-1,0.665]=[0.0903,-0.7553,0.665]，是不是非常简单！！然后再根据这个进行back propagation就可以了