HDU3338：Kakuro Extension（最大流）

Kakuro Extension

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2847    Accepted Submission(s): 983
Special Judge

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3338

Description：

If you solved problem like this, forget it.Because you need to use a completely different algorithm to solve the following one.
Kakuro puzzle is played on a grid of "black" and "white" cells. Apart from the top row and leftmost column which are entirely black, the grid has some amount of white cells which form "runs" and some amount of black cells. "Run" is a vertical or horizontal maximal one-lined block of adjacent white cells. Each row and column of the puzzle can contain more than one "run". Every white cell belongs to exactly two runs — one horizontal and one vertical run. Each horizontal "run" always has a number in the black half-cell to its immediate left, and each vertical "run" always has a number in the black half-cell immediately above it. These numbers are located in "black" cells and are called "clues".The rules of the puzzle are simple:

1.place a single digit from 1 to 9 in each "white" cell
2.for all runs, the sum of all digits in a "run" must match the clue associated with the "run"

Given the grid, your task is to find a solution for the puzzle.
　　　　　　　　 　　　　　
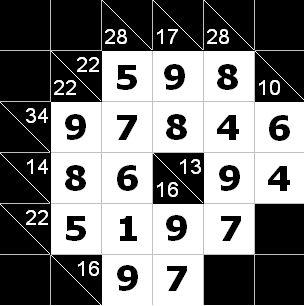
　　　　　　　　Picture of the first sample input　　　　　　　　　　　　Picture of the first sample output

Input:

Print n lines to the output with m cells in each line. For every "black" cell print '_' (underscore), for every "white" cell print the corresponding digit from the solution. Delimit cells with a single space, so that each row consists of 2m-1 characters.If there are many solutions, you may output any of them.

Sample Input:

6 6

XXXXXXX XXXXXXX 028\XXX 017\XXX 028\XXX XXXXXXX

XXXXXXX 022\022 ....... ....... ....... 010\XXX

XXX\034 ....... ....... ....... ....... .......

XXX\014 ....... ....... 016\013 ....... .......

XXX\022 ....... ....... ....... ....... XXXXXXX

XXXXXXX XXX\016 ....... ....... XXXXXXX XXXXXXX

5 8

XXXXXXX 001\XXX 020\XXX 027\XXX 021\XXX 028\XXX 014\XXX 024\XXX

XXX\035 ....... ....... ....... ....... ....... ....... .......

XXXXXXX 007\034 ....... ....... ....... ....... ....... .......

XXX\043 ....... ....... ....... ....... ....... ....... .......

XXX\030 ....... ....... ....... ....... ....... ....... XXXXXXX

Sample Output:

_ _ _ _ _ _

_ _ 5 8 9 _

_ 7 6 9 8 4

_ 6 8 _ 7 6

_ 9 2 7 4 _

_ _ 7 9 _ _

 

 

_ _ _ _ _ _ _ _

_ 1 9 9 1 1 8 6

_ _ 1 7 7 9 1 9

_ 1 3 9 9 9 3 9

_ 6 7 2 4 9 2 _

题意：

给出一个n*m的矩阵，"......."代表我们将在这里放一个1-9的数字，然后其它的都代表一个障碍，有些障碍上面有数字，如果数字在最后三位，代表了这个障碍右边所放数字之和为那个三位数（遇到障碍截止）。如果数字在前三位，那么说明下面的一连串数字之和为它。

现在就要求你放入数字满足条件，注意这里使special judge。

题解:

由于这是一个矩阵，我们建图时想着行列匹配，每一行有一个权值等于前面障碍的三个数字，对于每一列也一样。

但是由于中间有障碍，所以我们考虑重新构建一个行和列，对于一个横排，遇到障碍就分行；对于一个竖排，遇到障碍也分行。

这中间我们要用各种数组记录一下新行列和旧行列...

然后源点连每一行，汇点连每一列，容量为相应的三位数。

但凡要放数字的行列，我们都连一条容量为8的边。

注意这里不是9，因为如果连容量为9的话，流可以从0-9就是10种情况了；另外如果连容量为9，那么流的下限就为1。为了减去不必要的麻烦，我们连容量为8的边。

代码最好自己实现，这种题看别人代码会看晕的...

代码如下：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <queue>
#define INF 99999999
#define t 50000
using namespace std;
typedef long long ll;
const int N = ,M = 5e4+;
int n,m,tot;
int head[M],map[N][N],num[N][N],r[M],c[M],vr[M],vc[M],d[M],pr[M],pc[M],ans[N][N];
//num:将点离散化
//r,c:离散化后的点 新的行,列
//vr,vc:行,列的值
//pr,pc:新的行,列在原图中的行列
char s[N][N][];
struct Edge{
    int v,next,c;
}e[M];
void adde(int u,int v,int c){
    e[tot].v=v;e[tot].c=c;e[tot].next=head[u];head[u]=tot++;
    e[tot].v=u;e[tot].c=;e[tot].next=head[v];head[v]=tot++;
}
int cal(char x,char y,char z){
    return (x-'')*+(y-'')*+z-'';
}
int bfs(){
    memset(d,,sizeof(d));d[]=;
    queue <int > q;q.push();
    while(!q.empty()){
        int u=q.front();q.pop();
        for(int i=head[u];i!=-;i=e[i].next){
            int v=e[i].v;
            if(e[i].c> && !d[v]){
                d[v]=d[u]+;
                q.push(v);
            }
        }
    }
    return d[t]!=;
}
int dfs(int s,int a){
    if(s==t || a==) return a;
    int flow=,f;
    for(int i=head[s];i!=-;i=e[i].next){
        int v=e[i].v;
        if(d[v]!=d[s]+) continue ;
        f=dfs(v,min(a,e[i].c));
        if(f>){
            e[i].c-=f;
            e[i^].c+=f;
            flow+=f;
            a-=f;
            if(a==) break;
        }
    }
    if(!flow) d[s]=-;
    return flow;
}
int Dinic(){
    int flow=;
    while(bfs()) flow+=dfs(,INF);
    return flow;
}
int main(){
    while(scanf("%d%d",&n,&m)!=EOF){
        tot = ;memset(head,-,sizeof(head));memset(map,,sizeof(map));
        memset(num,,sizeof(num));int Num=;
        for(int i=;i<=n;i++){
            for(int j=;j<=m;j++){
                scanf("%s",s[i][j]);
                if(s[i][j][]=='.') map[i][j]=;
                else if(s[i][j][]=='X' && s[i][j][]=='X') map[i][j]=;
                else map[i][j]=;
                num[i][j]=++Num;
            }
        }
        memset(r,,sizeof(r));memset(c,,sizeof(c));
        memset(pr,,sizeof(pr));memset(pc,,sizeof(pc));
        int nr=,nc=;
        for(int i=;i<=n;i++){
            int k;
            for(int j=;j<=m;j++){
                int tmp = ;
                if(map[i][j]==){
                    nr++;
                    pr[nr]=i;
                    char x=s[i][j-][],y=s[i][j-][],z=s[i][j-][];
                    int now = cal(x,y,z);
                    vr[nr]=now;
                    for(k=j;k<=m;k++){
                        if(map[i][k]==) r[num[i][k]]=nr,tmp++;
                        else break ;
                    }
                    j=k;
                    vr[nr]-=tmp;
                }
            }
        }
        for(int i=;i<=m;i++){
            int k;
            for(int j=;j<=n;j++){
                int tmp = ;
                if(map[j][i]==){
                    nc++;
                    pc[nc]=i;
                    char x=s[j-][i][],y=s[j-][i][],z=s[j-][i][];
                    int now = cal(x,y,z);
                    vc[nc]=now;
                    for(k=j;k<=n;k++){
                        if(map[k][i]==) c[num[k][i]]=nc,tmp++;
                        else break ;
                    }
                    j=k;
                    vc[nc]-=tmp;
                }
            }
        }
        for(int i=;i<=nr;i++) adde(,i,vr[i]);
        for(int i=;i<=nc;i++) adde(nr+i,t,vc[i]);
        for(int i=;i<=n;i++){
            for(int j=;j<=m;j++){
                if(map[i][j]==){
                    int u=r[(i-)*m+j],v=c[(i-)*m+j];
                    adde(u,nr+v,);
                }
            }
        }
        Dinic();
        memset(ans,,sizeof(ans));
        for(int u=;u<=nr;u++){
            for(int i=head[u];i!=-;i=e[i].next){
                int v=e[i].v;
                if(v<=nr) continue ;
                v-=nr;
                int nowr = pr[u],nowc = pc[v];
                if(map[nowr][nowc])ans[nowr][nowc]=e[i].c;
            }
        }
        for(int i=;i<=n;i++){
            for(int j=;j<=m;j++){
                if(map[i][j]!=) printf("_ ");
                else printf("%d ",-ans[i][j]);
            }
            printf("\n");
        }
    }
    return ;
}