LibreOJ 6278 数列分块入门 2(分块)

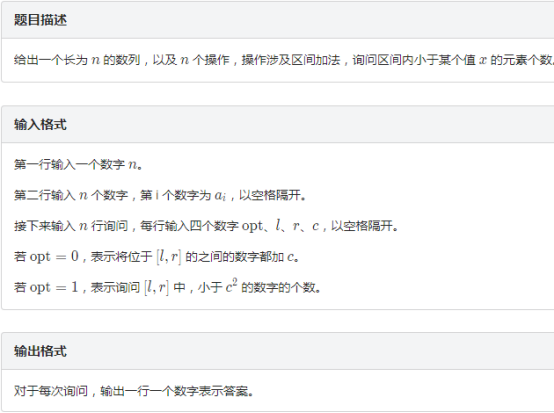
 题解:非常高妙的分块,每个块对应一个桶,桶内元素全部sort过,加值时,对于零散块O(sqrt(n))暴力修改,然后暴力重构桶.对于大块直接整块加.查询时对于非完整块O(sqrt(n))暴力遍历.对于完整的大块用lower_bound或者手写二分log(sqrt(n)查找,总复杂度O(n*sqrt(n)*log(sqrt(n)))

代码如下:

#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

int a[],lump[],tag[];
int n,sz;
vector<int> v[];

void reset(int x)
{
    v[x].clear();
    for(int i=(x-)*sz+;i<=min(x*sz,n);i++)
    {
        v[x].push_back(a[i]);
    }
    sort(v[x].begin(),v[x].end());
}

void add(int l,int r,int c)
{
    for(int i=l;i<=min(lump[l]*sz,r);i++)
    {
        a[i]+=c;
    }
    reset(lump[l]);
    if(lump[l]!=lump[r])
    {
        for(int i=(lump[r]-)*sz+;i<=r;i++)
        {
            a[i]+=c;
        }
        reset(lump[r]);
    }
    for(int i=lump[l]+;i<=lump[r]-;i++)
    {
        tag[i]+=c;
    }
} 

int query(int l,int r,int c)
{
    int ans=;
    for(int i=l;i<=min(lump[l]*sz,r);i++)
    {
        if(a[i]+tag[lump[l]]<c)
        {
            ans++;
        }
    }
    if(lump[l]!=lump[r])
    {
        for(int i=(lump[r]-)*sz+;i<=r;i++)
        {
            if(a[i]+tag[lump[r]]<c)
            {
                ans++;
            }
        }
    }
    for(int i=lump[l]+;i<=lump[r]-;i++)
    {
        int z=c-tag[i];
        ans+=lower_bound(v[i].begin(),v[i].end(),z)-v[i].begin();
    }
    return ans;
}

int main()
{
    int opt,l,r,c;
    scanf("%d",&n);
    sz=sqrt(n);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    for(int i=;i<=n;i++)
    {
        lump[i]=(i-)/sz+;
        v[lump[i]].push_back(a[i]);
    }
    for(int i=;i<=lump[n];i++)
    {
        sort(v[i].begin(),v[i].end());
    }
    for(int i=;i<=n;i++)
    {
        scanf("%d%d%d%d",&opt,&l,&r,&c);
        if(!opt)
        {
            add(l,r,c);
        }
        else
        {
            printf("%d\n",query(l,r,c*c));
        }
    }
}