1D/1D优化dp之利用决策点的凸性优化

关于dp的优化之前做过一些简单的利用优先队列或者单调队列维护一个值就ok了，但有时候给出的方程很难直接用单调队列维护，需要转化一下思路。

这种优化方式利用数形结合，根据比较斜率来抛去一些非最优解，能将方程优化到线性，但对于一些更难得题目就需要一些数据结构维护，我暂时没接触过。

先用一道简单的题目来入手，hdu 3507 http://acm.hdu.edu.cn/showproblem.php?pid=3507

Print Article

Time Limit: 9000/3000 MS (Java/Others)    Memory Limit: 131072/65536 K (Java/Others)
Total Submission(s): 13750    Accepted Submission(s): 4247

Problem Description

Zero
has an old printer that doesn't work well sometimes. As it is antique,
he still like to use it to print articles. But it is too old to work for
a long time and it will certainly wear and tear, so Zero use a cost to
evaluate this degree.
One day Zero want to print an article which has
N words, and each word i has a cost Ci to be printed. Also, Zero know
that print k words in one line will cost

M is a const number.
Now Zero want to know the minimum cost in order to arrange the article perfectly.

 

Input

There are many test cases. For each test case, There are two numbers N and M in the first line (0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000). Then, there are N numbers in the next 2 to N + 1 lines. Input are terminated by EOF.

 

Output

A single number, meaning the mininum cost to print the article.

 

Sample Input

5 5
5
9
5
7
5

 

Sample Output

230

      一个显然的方程就是 f[i]=MIN{ f[j]+M+(sum[j]-sum[i])^2  },复杂度O(N^2) 显然也会T。令 k<j<i ，不妨假设如果j点作为决策点比k更优的话需要满足什么条件，显然是

f[j]+(sum[j]-sum[i])^2 < f[k]+(sum[k]-sum[i])^2   --->    f[j]+sum[j]^2-(f[k]+sum[k]^2) < 2*sum[i]*(sum[j]-sum[k] )  -------> 即  g(k,j)= ( (f[j]+sum[j]^2)-(f[k]+sum[k]^2) ) / (sum[j]-sum[k]) < 2*sum[i];

由此我们得到了一个判别式g(k,j),如果 k<j<i&&g(k,j)<2*sum[i]就足以说明j优于k。

    令yj=f[j]+sum[j]^2, x[j]=sum[j],  那么简写为 (yj-yk)/(xj-xk)<2*sum[i], 像极了斜率的推导公式。从这个式子中我们得到一些性质，由于sum[i]是显然递增的，所以当前状态下如果j优于k那么

在后面的状态中j始终会优于k所以我们可以抛去k  -> 1.if(g(k,j)<=2*sum[i]) pop(k)               //ps.相等时二者等价所以可以删去        2.if(g(k,j)>=g(j,i)) pop(j)  关于这个的正确性在于

如果g(j,i)<=2*sum,显然i优于等于j； 如果g(j,i)>2*sum，那么g(k,j)>2*sum ,所以k优于j，综上 j是无用点，所以可以抛去。

   有一个重要的性质在于: 所有最优决策点都在平面点集的凸包上。

令ai=-2*sum[i],xj=sum[j],yj=f[j]+sum[j],  那么min{p}=ax+y -->  y=p-ax, 当在y轴上的截距最小时有最优解p，相当于把每个sum[i]和对应的最优解当作了一个点。

 

 

 

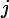
将小于j的点画在平面直角坐标系上，一如线性规划，把这条斜线自下往上平移时遇到的第一个点，即能使目前状态有最小值的点。于是我们需要维护一个下凸壳，把那些肯定不会贡献的点删掉。

   根据上面的推倒代码就很好写了。

 #include<bits/stdc++.h>
 using namespace std;
 #define qz q.size()
 int f[];
 int sum[];
 deque<int>q;
 int dy(int i,int j){return f[j]-f[i]+sum[j]*sum[j]-sum[i]*sum[i];}
 int dx(int i,int j){return sum[j]-sum[i];}
 int main()
 {
     int N,M,i;
     while(scanf("%d%d",&N,&M)==){
         q.clear();
         q.push_back();
         for(i=;i<=N;++i)
         {
             scanf("%d",sum+i);
             sum[i]+=sum[i-];
          while(qz>&&dy(q[],q[])<=*dx(q[],q[])*sum[i]) q.pop_front();
          f[i]=f[q.front()]+M+(sum[i]-sum[q.front()])*(sum[i]-sum[q.front()]);
          while(qz>&&dy(q[qz-],i)*dx(q[qz-],q[qz-])<=dy(q[qz-],q[qz-])*dx(q[qz-],i))q.pop_back();
          q.push_back(i);
         }
         printf("%d\n",f[N]);
     }
     return ;
 }

   bzoj 1010  http://www.lydsy.com/JudgeOnline/problem.php?id=1010

和上面的做法类似。

 #include<bits/stdc++.h>
 using namespace std;
 #define LL long long
 #define qz q.size()
 LL f[];
 LL sum[];
 int N,L;
 deque<int>q;
 LL dy(int i,int j,int a){
     return (f[j]+(sum[j]-(a-j+-L))*(sum[j]-(a-j+-L)))-(f[i]+(sum[i]-(a-i+-L))*(sum[i]-(a-i+-L)));
     }
 LL dx(int i,int j,int a){return (sum[j]-(a-j+-L))-(sum[i]-(a-i+-L));}
 int main()
 {
     int i;
     while(scanf("%d%d",&N,&L)==){
         q.clear();
         q.push_back();
         for(i=;i<=N;++i)
         {
             scanf("%d",sum+i);
             sum[i]+=sum[i-];
         }
         for(i=;i<=N;++i)
         {
          while(qz>&&dy(q[],q[],i)<=*dx(q[],q[],i)*sum[i]) q.pop_front();
          f[i]=f[q[]]+(sum[i]-sum[q[]]+i-q[]--L)*(sum[i]-sum[q[]]+i-q[]--L);
          while(qz>&&dy(q[qz-],i,i)*dx(q[qz-],q[qz-],i)<=dy(q[qz-],q[qz-],i)*dx(q[qz-],i,i))q.pop_back();
          q.push_back(i);
         }
         printf("%lld\n",f[N]);
     }
     return ;
 }