codeforces734E

题目连接：http://codeforces.com/contest/734/problem/E

E. Anton and Tree

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Anton is growing a tree in his garden. In case you forgot, the tree is a connected acyclic undirected graph.

There are n vertices in the tree, each of them is painted black or white. Anton doesn't like multicolored trees, so he wants to change the tree such that all vertices have the same color (black or white).

To change the colors Anton can use only operations of one type. We denote it as paint(v), where v is some vertex of the tree. This operation changes the color of all vertices u such that all vertices on the shortest path from v to u have the same color (including v and u). For example, consider the tree

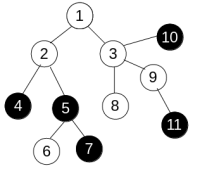
and apply operation paint(3) to get the following:

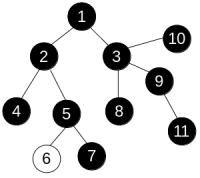
Anton is interested in the minimum number of operation he needs to perform in order to make the colors of all vertices equal.

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 200 000) — the number of vertices in the tree.

The second line contains n integers color_i (0 ≤ color_i ≤ 1) — colors of the vertices. color_i = 0 means that the i-th vertex is initially painted white, while color_i = 1 means it's initially painted black.

Then follow n - 1 line, each of them contains a pair of integers u_i and v_i (1 ≤ u_i, v_i ≤ n, u_i ≠ v_i) — indices of vertices connected by the corresponding edge. It's guaranteed that all pairs (u_i, v_i) are distinct, i.e. there are no multiple edges.

Output

Print one integer — the minimum number of operations Anton has to apply in order to make all vertices of the tree black or all vertices of the tree white.

题目大意：有一棵树，有黑白两种颜色，每个节点为黑色或白色，每次变换使得相连的同色节点全部变成另一种颜色，求使树变成单色（纯黑或纯白）所需的最少操作数。

解题思路：

刚开始忽略了改变颜色后连同块的大小会改变，用并查集做了，结果当然WA，后来想到会改变，所以用dfs。

第一次dfs缩点，把连通块缩为一点，构成一个新图，方便处理。

缩点完成后的图就变成了黑白交替出现的一棵树，改变一个节点就相当于把它和与他直接相连的所有节点缩为一点，最后的结果为该树的最长路径/2。

写一下自己想的弱鸡证明过程；

1.首先证明，操作次数只与最长路径有关。

假设有一棵树（称之为完全树），在它的最长路径上的所有节点都连有在保证该路径是最长路径的前提下可连的最多节点，显然，此种情况下操作次数不会大于只有最长路的操作次数，因为必须保证最长链完成修改。另外显然，经过缩点得到的所有可能的树的操作次数小于等于完全树，所以可得，操作次数只与最长路径有关。

2.证明结果为最长路径的1/2。

只考虑其最长路径，假设最长路径节点数n为奇数，则相当于每次操作减少两节点，直至最后剩下一个节点，设操作数为x，则有：n-2x=1，解得x=(n-1)/2;

假设n为偶数，则最后一次操作相当于只消除一个节点，则有n-2(x-1)-1=1,解得 =n/2

综合可得，x=n/2（整数除法）

代码如下：

#include<bits/stdc++.h>

using namespace std;

vector <],g[];
];
]={};
,maxp;

void dfs1(int n,int s)
{
    if(n>N||vis[n])
        return;
    vis[n]=;
    if(c[n]!=c[s])
    {
        g[n].push_back(s);
        g[s].push_back(n);
        s=n;
    }
    ;i<G[n].size();i++)
    {
        dfs1(G[n][i],s);
    }
}

void dfs2(int n,int dis)
{
    if(vis[n])
        return;
    vis[n]=;
    if(dis>maxx)
    {
        maxx=dis;
        maxp=n;
    }
    ;i<g[n].size();i++)
        dfs2(g[n][i],dis+);
}

int main()
{
    int x,y;
    cin>>N;
    ;i<=N;i++)
        scanf("%d",&c[i]);
    ;i<N;i++)
    {
        scanf("%d%d",&x,&y);
        G[x].push_back(y);
        G[y].push_back(x);
    }
    dfs1(,);
    memset(vis,,sizeof(vis));
    dfs2(,);
    memset(vis,,sizeof(vis));
    dfs2(maxp,);
    cout<<maxx/<<endl;
}