AIM Tech Round 5 (rated, Div. 1 + Div. 2) C. Rectangles 【矩阵交集】

题目传传传送门：http://codeforces.com/contest/1028/problem/C

C. Rectangles

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given nn rectangles on a plane with coordinates of their bottom left and upper right points. Some (n−1)(n−1) of the given nn rectangles have some common point. A point belongs to a rectangle if this point is strictly inside the rectangle or belongs to its boundary.

Find any point with integer coordinates that belongs to at least (n−1)(n−1) given rectangles.

Input

The first line contains a single integer nn (2≤n≤1326742≤n≤132674) — the number of given rectangles.

Each the next nn lines contains four integers x1x1, y1y1, x2x2 and y2y2 (−109≤x1<x2≤109−109≤x1<x2≤109, −109≤y1<y2≤109−109≤y1<y2≤109) — the coordinates of the bottom left and upper right corners of a rectangle.

Output

Print two integers xx and yy — the coordinates of any point that belongs to at least (n−1)(n−1) given rectangles.

Examples

input

Copy

3
0 0 1 1
1 1 2 2
3 0 4 1

output

Copy

1 1

input

Copy

3
0 0 1 1
0 1 1 2
1 0 2 1

output

Copy

1 1

input

Copy

4
0 0 5 5
0 0 4 4
1 1 4 4
1 1 4 4

output

Copy

1 1

input

Copy

5
0 0 10 8
1 2 6 7
2 3 5 6
3 4 4 5
8 1 9 2

output

Copy

3 4

Note

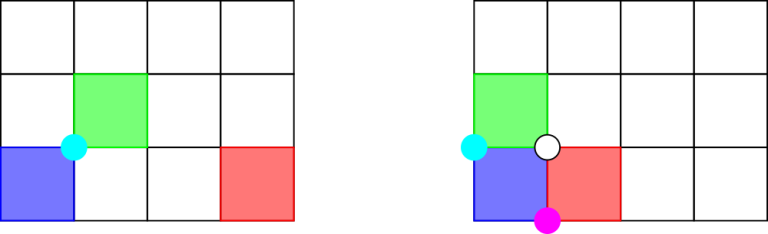
The picture below shows the rectangles in the first and second samples. The possible answers are highlighted.

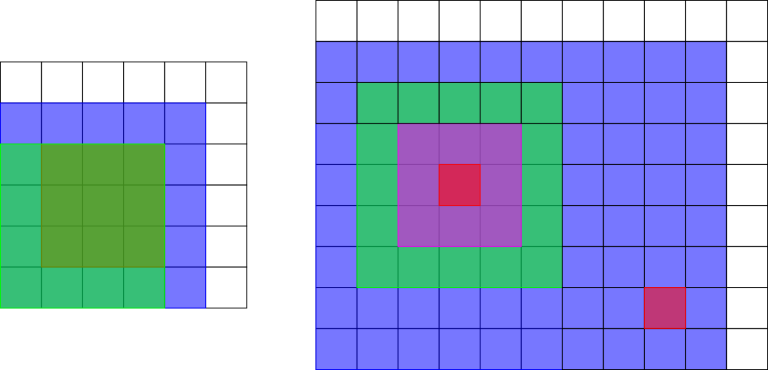
The picture below shows the rectangles in the third and fourth samples.

题意概括：

N个矩阵，每个矩阵的表示方法是给左下角和右上角的坐标，求一个点至少在（N-1）个矩阵内部，求这个点的坐标（如果有多个输出其中一个就可以了）。

解题思路：

比赛时TLE的思路是二维树状数组标记，然后查询找被标记了至少（N-1）次的点。

TLE code：

 #include <cstdio>
 #include <iostream>
 #include <algorithm>
 #include <cstring>
 #include <cmath>
 #include <map>
 #define ll long long int;
 #define INF 0x3f3f3f3f
 using namespace std;
 const int MAXN = ;
 const int MAX = 1e9;
 int x[MAXN], y[MAXN];
 map<int,map<int, int> >mmp;
 int N, T;

 int lowbit(int x)
 {
     return x&(-x);
 }

 void add(int x, int y, int value)
 {
     for(int i = x; i <= MAX; i += lowbit(i))
     for(int j = y; j <= MAX; j += lowbit(j))
         mmp[i][j] += value;
 }

 int sum(int x, int y)
 {
     int res = ;
     for(int i = x; i > ; i -= lowbit(i))
     for(int j = y; j > ; j -= lowbit(j))
         res+=mmp[i][j];
     return res;
 }

 void init()
 {
     for(int i = ; i <= N; i++)
         for(int j = ; j <= N; j++)
         mmp[i][j] = ;
 }

 int main()
 {
     int x1, y1, x2, y2;
     scanf("%d", &N);
     for(int i = ; i <= N; i++)
     {
         scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
         x1++, x2++, y1++, y2++;
         x[i] = x1;
         y[i] = y1;
         add(x1, y1, );
         add(x2+, y1, -);
         add(x1, y2+, -);
         add(x2+, y2+, -);
     }
     for(int i = ; i <= N; i++)
     {
         if(sum(x[i], y[i]) >= N-)
         {
             printf("%d %d", x[i]-, y[i]-);
             break;
         }
     }
     return ;
 }

然而这道题其实是道YY题...求矩阵前缀交集和后缀交集，然后 O(n) 枚举每一个点不在交集中的情况（也就是该点前缀交后缀的情况），如果该点不在时存在合法交集，那么答案就出来了。

AC code：

 #include <bits/stdc++.h>
 #define INF 0x3f3f3f3f
 #define LL long long int
 using namespace std;
 const int MAXN = ;
 typedef struct Date{
     int x1, x2, y1, y2;
 };
 Date P[MAXN], st[MAXN], ed[MAXN];
 int N;

 inline Date add(Date a, Date b)
 {
     Date res;
     res.x1 = max(a.x1, b.x1);
     res.y1 = max(a.y1, b.y1);
     res.x2 = min(a.x2, b.x2);
     res.y2 = min(a.y2, b.y2);
     return res;
 }

 int main()
 {
     scanf("%d", &N);
     for(int i = ; i <= N; i++)
     {
         scanf("%d%d%d%d", &P[i].x1, &P[i].y1, &P[i].x2, &P[i].y2);
     }
     st[] = P[]; ed[N] = P[N];
     for(int i = ; i <= N; i++) st[i] = add(st[i-], P[i]);
     for(int i = N-; i >= ; i--) ed[i] = add(ed[i+], P[i]);

     for(int i = ; i <= N; i++){
         Date cur;
         if(i == ) cur = ed[];
         else if(i == N) cur = st[N-];
         else cur = add(st[i-], ed[i+]);
         if(cur.x1 <= cur.x2 && cur.y1 <= cur.y2){
             printf("%d %d\n", cur.x1, cur.y1);
             break;
         }
     }
     return ;
 }