EXKMP学习笔记QAQ

@

目录

• 定义
• 算法思想
• 疑难杂症
• 练习题目
  • 双倍经验
  • 应用
    • 正确性：
    • 优化：
• 小结

因为一本通少了一些算法，所以我就自行补充了一些东西上去。

EXKMP也就是扩展KMP，是一种特别毒瘤的东西

EXKMP确实很难，我理解他的时间与AC机的时间差不多，而且还很难记，因此一学会就马上写博客了QAQ

定义

例题

EXKMP就是解决这种问题的。

先讲两个数组的定义（默认所有数组从1开始）：

ex数组，代表A（主串）的从第i位与B（子串）的最长相同前缀。

next数组，代表B（子串）的从第i位与B（子串）的最长相同前缀。

算法思想

注：所有字符串下标从1开始

首先，假定已经匹配的ex数组位置为1~a，next数组全部匹配好了（next数组的匹配方式跟ex数组的匹配方式大致相同，后面会讲，不用担心）。

首先，我们定义一个\(p\)，代表\(max(i+ex_{i}-1)(i\in [1,a])\)，也就是目前在主串中匹配到的最远的位置，同时设能使p最大的\(i\)为\(b\)，设目前要匹配\(k\)的位置。

首先，我们知道，当\(a<=p\)时，那么我们可以知道\(A_{b\rightarrow p}=B_{1\rightarrow (p-a+1)}\)。

注：至于\(a==p+1\)的情况仅当\(ex_{a}=0\)并且以前的\(i+ex_{i}-1\)都没有超过\(a-1\)，且在这种情况下，在后面会讲到，将被归类在\(k+L>=p\)中\(k>p\)的情况，不会造成任何任何影响，后面会讲，无需着急，同时不会有\(a>p-1\)的情况。

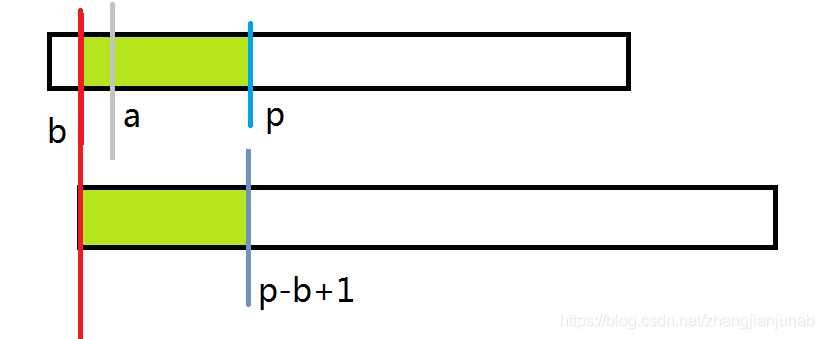
注：上面是B串，下面是A串，绿色部分为相等部分。

那么，我们去掉一起从开头去掉\(k-b\)长度的字符串，即为\(A_{k\rightarrow p}=B_{(k-b+1)\rightarrow (p-a+1)}\)（紫色部分）

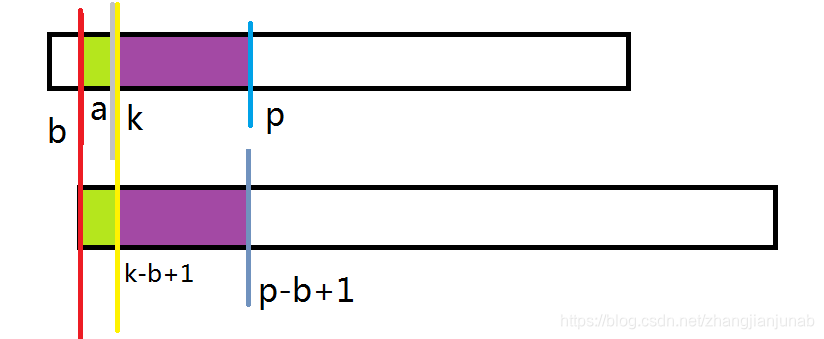
注：为什么\(k\)挨着\(a\)？因为\(k=a+1\)，这里为证明方便，多设一个k。

但是，我们并不知道从A串从\(k\)开始的地方与B串从\(1\)开始的地方有什么瓜葛？

这时候，我们需要一员大将：设\(L=next_{k-b+1}\)，没错，我们知道了\(A_{k\rightarrow p}=B_{(k-b+1)\rightarrow (p-a+1)}\)，那么我们就可以找出从\(B_{1}\)开始最长可以与\(B_{(k-b+1)}\)相等多少，就是next数组。

这时候，有了两种情况：

先设\(now=k+L-1\)。

1. now<p

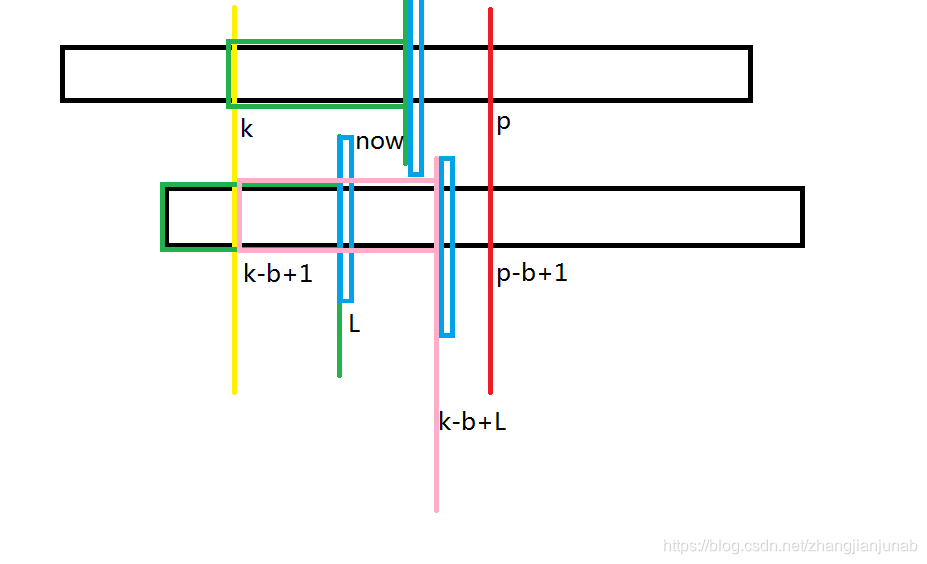
注：上面是B串，下面是A串，粉色框框与绿色框框为相等部分。

我们发现，三个蓝色部分：\(B_{(now+1)},A_{(L+1)},A_{(k-b+L+1)}\)，根据前面，我们知道：\(B_{(now+1)}=A_{(k-b+L+1)}\)，有根据next数组的定义，我们知道\(A_{(L+1)}\ne A_{(k-b+L+1)}\)（如果不是的话，L可以++），那么，我们可以知道\(A_{(L+1)}\ne B_{(now+1)}\)，所以，这个时候\(ex_{k}=L\)。

1. now>p

这也分两种情况：

1. k>p

这个时候应当从\(k\)开始暴力匹配，因为\(k\)不在\(p\)的范围内，\(k-b+1\)也不在\(p-b+1\)的范围内，所以只能暴力匹配。

2.k≤p

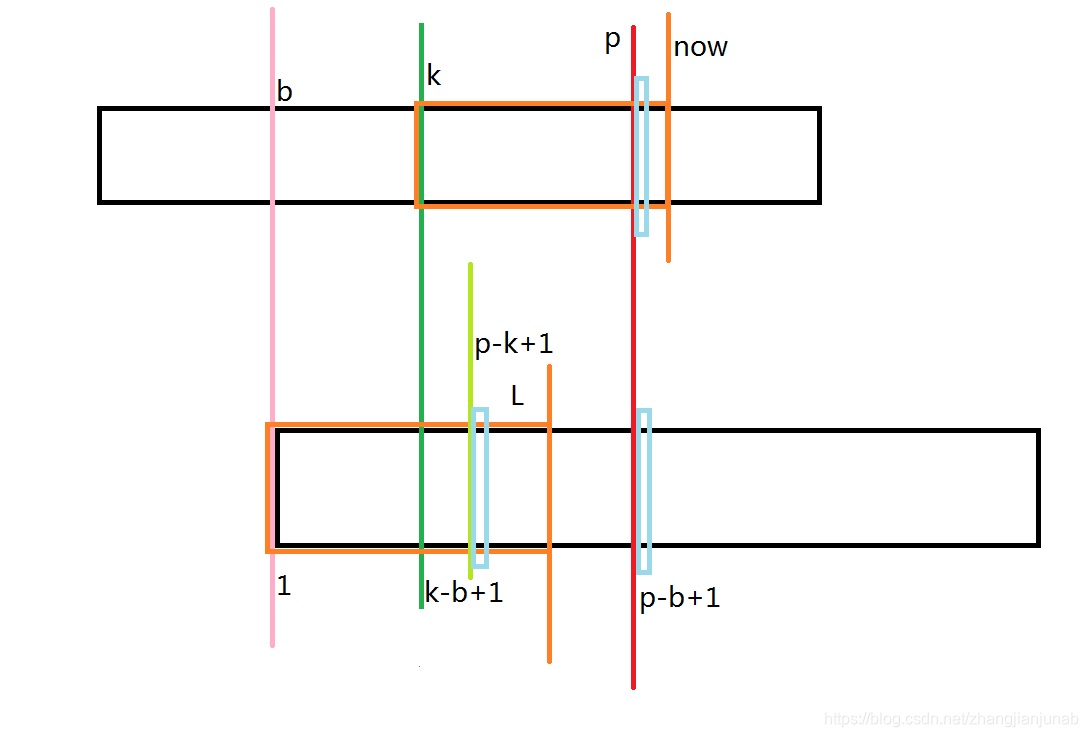
首先，我们知道now>p，意味着什么？你真的学会的话，应该知道如果now>p，那么\(k-b+1+L-1=k-b+L>(p-b+1)\)。

那么，这里面的\(p-k+1\)其实就是在\(B_{1}\)至\(B_{L}\)中与\(B_{p-b+1}\)所对应的位置，也就是与\(A_{p}\)所对应的位置。

那么我们就知道了三个关键位置\(A_{p},B_{p-k+1},B_{p-b+1}\)，我们看他后面的浅蓝色框框框住的位置\(A_{p+1},B_{p-k+2},B_{p-b+2}\)，像上一个那么推：\(A_{p+1}\ne B_{p-b+2},B_{p-b+2}=B_{p-k+2}\)，那么，我们就可以知道\(A_{p+1}\ne B_{p-k+2}\)，那么，这个时候我们就可以知道这时候\(ex_{k}=p-k+1\)

1. now=p

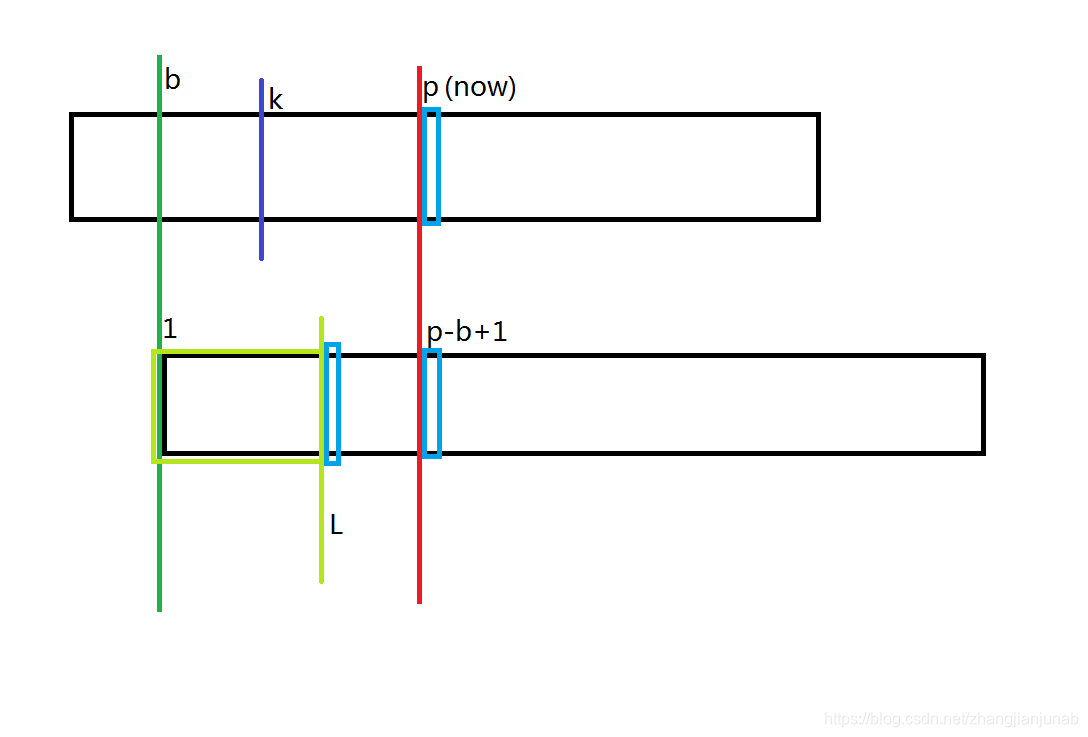
这种情况下，由于\(now==p\)，所以导致在\(B_{(p+1)},A_{(L+1)},A_{(p-b+2)}\)中，\(B_{(now+1)}\ne A_{(p-b+2)}\)，根据next数组的定义，我们知道\(A_{(L+1)}\ne A_{(p-b+2)}\)（如果不是的话，L可以++），但是\(A_{(p+1)}\ne B_{(L+1)}\)是不一定的。如\(a\ne b,b\ne a,a=b\)

那么，我们就直接等于p，然后不断暴力匹配，然后更新\(b\)、\(p\)、\(a\)。（其实\(a\)根本不需要记录的）

至于next如何匹配，就把B当成子串与主串就行了，不过\(next_{1}\)可以不用去理他。。。

复杂度：每个数匹配一次，\(p\)最多向右移到\(n\)（母串）。

当然，代码上有些细节，大家需要自行推倒一下：

#include<cstdio>
#include<cstring>
#define  N  1100000
using  namespace  std;
int  next[N],ex[1100000],n,m;
char  A[N],B[N];
inline  int  mymin(int  x,int  y){return  x<y?x:y;}
void  exkmp()
{
	//匹配next数组，由于next数组都为0，可以一开始不预处理出ex[2]。
	int  b=0,p=0;
	for(int  i=2;i<=m;i++)
	{
		int  L=next[i-b+1]/*i-b+1>1*/,now=i+L-1/*判断用的变量*/;
		if(now<p)next[i]=L;
		else//包括情况二与情况三
		{
			int  pp=p-i+1<0?0:p-i+1;
			while(i+pp<=m/*因为i+pp>pp+1(pp≥2)，所以判断i+pp就行了*/  &&  B[i+pp]==B[pp+1])pp++;
			next[i]=pp;b=i;p=next[b]+b-1;//更新
		}
	}
	b=p=0;//不用担心，他会跳到else里面去的
	for(int  i=1;i<=n;i++)
	{
		int  L=next[i-b+1],now=i+L-1;
		if(now<p)ex[i]=L;
		else
		{
			int  pp=p-i+1<0?0:p-i+1;
			while(i+pp<=n  &&  pp<m  &&  A[i+pp]==B[pp+1])pp++;
			ex[i]=pp;b=i;p=b+ex[b]-1;
		}
	}
}
int  main()
{
	scanf("%s%s",A+1,B+1);n=strlen(A+1);m=strlen(B+1);//输入
	exkmp();//匹配
	for(int  i=1;i<n;i++)printf("%d ",ex[i]);//输出
	printf("%d\n",ex[n]);
	return  0;
}

---

疑难杂症

没错，EXKMP就是这么难，于是我写了疑难杂症。其实就是自己太弱了，所以需要写。。。

1

代码中怎么只有情况一与情况三的代码？

因为我们发现情况二的代码可以在情况三的代码里面。

2

为什么不用预处理出\(ex\)数组与\(next\)数组的一个数字来更新\(b\)与\(p\)？

因为在一开始中，我们\(b=p=0\)

那么\(i+L-1\)就算\(i=1,L=0\)，\(i+L-1\)也大于\(1\)，所以我们可以放心的交给for循环。

3

困扰了我一段时间的一个问题，解决后发现是我想错方向，同时又想的太复杂的。

就是，当\(b\)与\(p\)更新了，在求原来的\(b-p\)与现在的\(b-p\)的交集的地方的时候，我们在求\(ex\)或\(next\)数组时，\(i-b+1\)是不同的，现在的\(b\)大于原来的\(b\)，那么现在的\(i-b+1\)就小于原来的\(i-b+1\)，是否会影响结果？

其实并不然，简单点，佛系思想：因为方法正确，只要是合法的\(b,p\)，都可以求出\(ex_{i}\)或\(next_{i}\)。

但是，深入一点想，更新了\(b\)与\(p\)，会不会影响求两个地方交集部分的\(ex\)或\(next\)？

画图帮助理解：

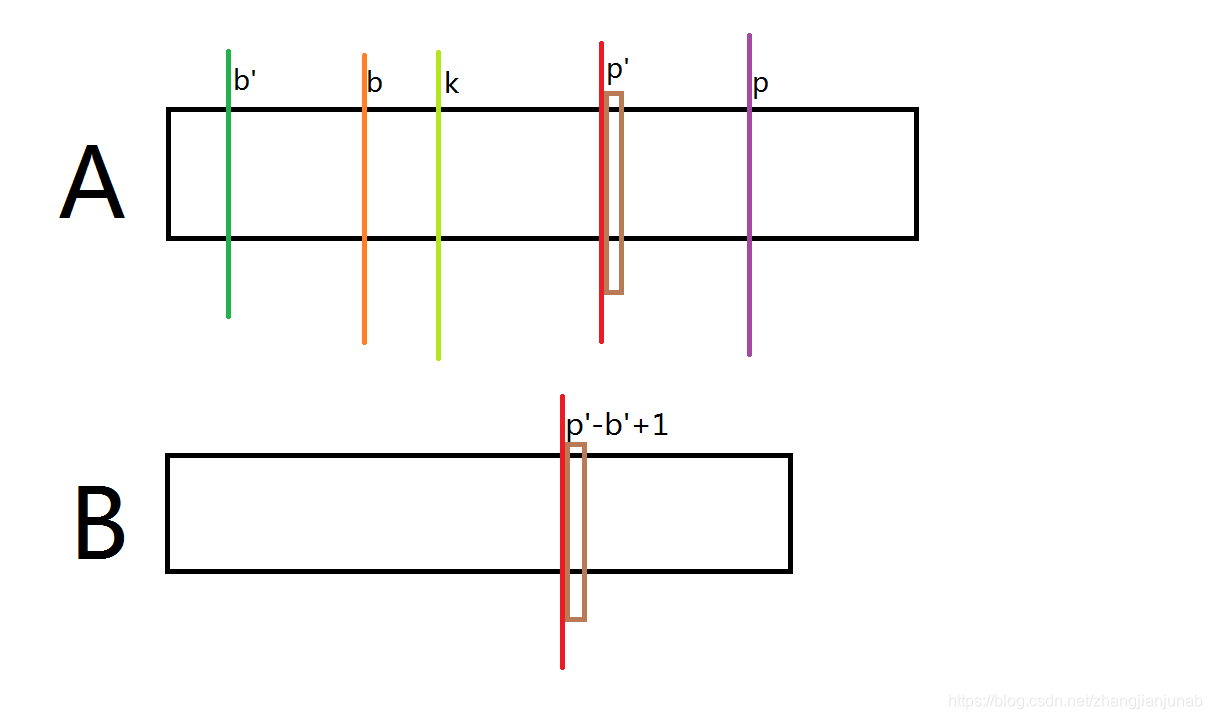
首先，棕色格子不相等，我们是知道的。

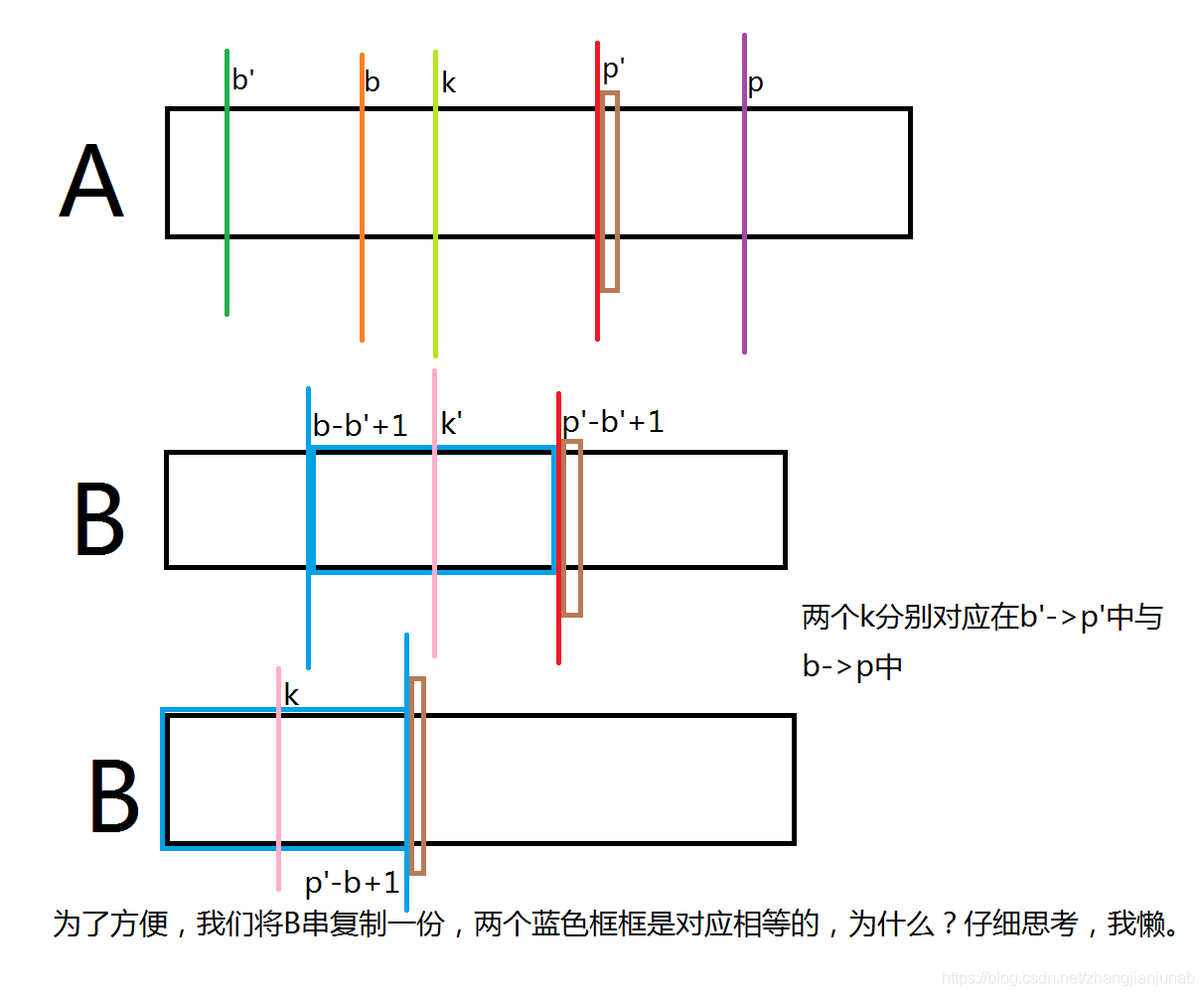
分三种情况考虑：

1. \(next_{k'}+k'-1＜p'-b'+1\)

这个时候，因为两个蓝色框框对应相等，所以\(next_{k}=next_{k'}\)。

2.\(next_{k'}+k'-1=p'-b'+1\)

这个时候，我们知道\(B_{p'-b'+2}\ne B_{next_{k'}+1}\)，又因为\(B_{p'-b'+2}\ne B_{p'-b+2}\)，那么，我们还是不知道\(B_{next_{k'}+1},B_{p'-b+2}\)的关系。。。那么\(k'+next_{k}+1≥p'-b'+1\)。

这种情况下匹配是否相等？

首先\(next_{k'}+k'-1=p'-b'+1\)，那么，在\(b'，p'\)的情况下，\(k\)会去暴力匹配，那么在\(b',p'\)的情况下，看\(next_{k}\)的情况，反正\(next_{k}≥next_{k'}\)，至少不会错，反而快了。

1. \(next_{k}+k'-1=p'-b'+1\)

照样像上面证明，得到\(next_{k'}+k'-1≥p'-b'+1\)，那么，我们知道\(p'≥p\)，首先\(next_{k}+k'-1=p'-b'+1\)，那么我们知道这时候\(now≤p\)，那么，在\(b,p\)中，最多暴力匹配或者跳到情况得到（匹配中的情况1，不是这里的情况1），而\(next_{k'}+k'-1≥p'-b'+1\)，那么，在\(b',p'\)中，\(k\)在A中的ex值也就是\(p'-k+1\)，可是在\(b,p\)中还有个暴力匹配的情况？

想想就知道，暴力匹配不会得出什么新的答案，最后结果还是\(p'-k+1\)

至此，问题3解决，完结撒花。

大家有什么问题可以在评论区问我。

---

练习题目

双倍经验

双倍经验

哈哈哈，双倍经验。

作为一道练手题目看待吧。

#include<cstdio>
#include<cstring>
#define  N  1100000
using  namespace  std;
int  next[N],ex[1100000],n,m;
char  A[N],B[N];
inline  int  mymin(int  x,int  y){return  x<y?x:y;}
void  exkmp()
{
	//匹配next数组，由于next数组都为0，可以一开始不预处理出ex[2]。
	int  b=0,p=0;
	for(int  i=2;i<=m;i++)
	{
		int  L=next[i-b+1]/*i-b+1>1*/,now=i+L-1/*判断用的变量*/;
		if(now<p)next[i]=L;
		else
		{
			int  pp=p-i+1<0?0:p-i+1;//代表目前从i位置已经匹配的长度。
			//里面有特判情况2中的情况2.
			while(i+pp<=m/*因为i+pp>pp+1(pp≥2)，所以判断i+pp就行了*/  &&  B[i+pp]==B[pp+1])pp++;
			next[i]=pp;b=i;p=next[b]+b-1;//更新
		}
	}
	//因为next数组匹配完了，要先处理出ex[1]
	b=p=0;//会跳到情况二
	//更匹配next差不多的代码
	for(int  i=1;i<=n;i++)
	{
		int  L=next[i-b+1],now=i+L-1;
		if(now<p)ex[i]=L;
		else
		{
			int  pp=p-i+1<0?0:p-i+1;
			while(i+pp<=n  &&  pp<m  &&  A[i+pp]==B[pp+1])pp++;
			ex[i]=pp;b=i;p=b+ex[b]-1;
		}
	}
}
int  main()
{
	scanf("%s%s",A+1,B+1);n=strlen(A+1);m=strlen(B+1);//输入
	exkmp();//匹配
	for(int  i=1;i<n;i++)printf("%d ",ex[i]);//输出
	printf("%d\n",ex[n]);
	return  0;
}

---

应用

EXKMP的应用

这道题目其实可以用Manacher来做的，但是毕竟标签是EXKMP，就用EXKMP来做。

首先，我们设\(A'\)是\(A\)倒过来的串，那么分别把\(A'\)与\(A\)当成主串或子串处理出两个ex数组。

至此，打架应该大概有思路了吧。

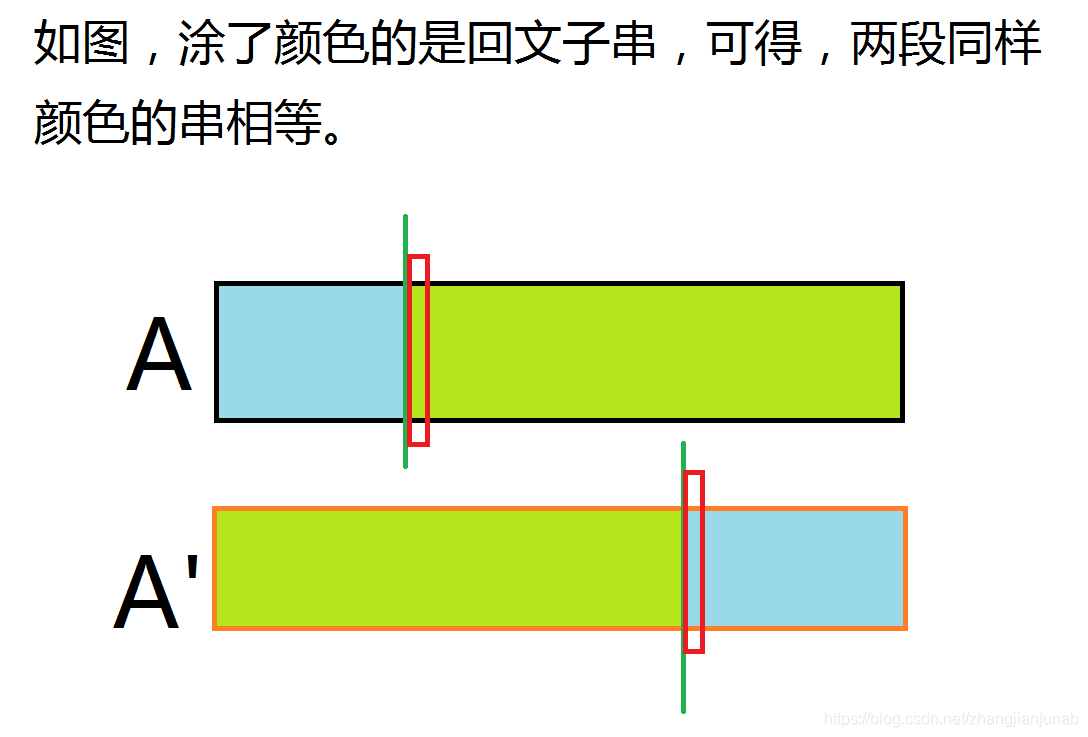
两个红色格子圈住的是重点，看\(A'\)串，假设\(A\)与\(A'\)的长度为\(n\)，蓝色部分长度为\(i\)，那么，我们可以看以\(A'_{(n-i+1)}\)为开头的前缀，与\(A\)串以\(A_{1}\)开头的那个前缀相等，且要求求出最长的长度。

仔细一看，不就是ex数组的定义？那么，我们可以由\(ex2_{(n-i+1)}\)得出，（ex2是以\(A\)为子串，\(A'\)主串的ex数组），那么我们仔细观察发现，当\(ex2_{(n-i+1)}≥(i/2)\)时，\(A\)中\([1,i]\)的子串就是一个回文子串。

至于如何判断\([i+1,n]\)的子串是否是回文子串，建议自己想，当然，图片中\(A\)串上也有一个红色框框框住的格子，方法与上面相同，也就不再赘述。作者越来越懒了。。。

#include<cstdio>
#include<cstring>
#define  N  510000
using  namespace  std;
char  st1[N],st2[N];
int  ex1[N],ex2[N],next[N],n;
inline  int  mymin(int  x,int  y){return  x<y?x:y;}
inline  int  mymax(int  x,int  y){return  x>y?x:y;}
void  exkmp(char  A[]/*母串*/,char  B[]/*母串*/,int  ex[]/*ex数组*/)//一遍exkmp
{
    //next
    int  b=0,p=0;
    for(int  i=2;i<=n;i++)//处理next
    {
        int  L=next[i-b+1],now=i+L-1;
        if(now<p)next[i]=L;
        else
        {
            int  qq=p-i+1<0?0:p-i+1;
            while(i+qq<=n  &&  B[i+qq]==B[qq+1])qq++;
            next[i]=qq;b=i;p=next[b]+b-1;
        }
    }
    //ex
    b=p=0;
    for(int  i=1;i<=n;i++)//处理ex
    {
        int  L=next[i-b+1],now=i+L-1;
        if(now<p)ex[i]=L;
        else
        {
            int  qq=p-i+1<0?0:p-i+1;
            while(i+qq<=n  &&  A[i+qq]==B[qq+1])qq++;
            ex[i]=qq;b=i;p=ex[b]+b-1;
        }
    }
}
int  d[30],sum[N];//处理权值和
int  main()
{
    int  T;scanf("%d",&T);
    while(T--)
    {
        for(int  i=1;i<=26;i++)scanf("%d",&d[i]);
        scanf("%s",st1+1);n=strlen(st1+1);
        for(int  i=1;i<=n;i++)st2[i]=st1[n-i+1],sum[i]=sum[i-1]+d[st1[i]-'a'+1];//倒着的串
        exkmp(st1,st2,ex1);exkmp(st2,st1,ex2);//处理正着跟倒着
        int  ans=0;
        for(int  i=1;i<n;i++)//暴力处理最大值
        {
            int  now=0;
            if(ex2[n-i+1]>=i/2)now+=sum[i];//判断[1,i]是否是回文串
            if(ex1[i+1]>=(n-i)/2)now+=sum[n]-sum[i];//判断[i+1,n]是否是回文串
            ans=mymax(ans,now);//更新
        }
        printf("%d\n",ans);
    }
    return  0;
}

---

练习1

这道题目，嗯，十分牛逼，用kmp可以解决，但是时间是EXKMP的两倍。

EXKMP怎么做？

先看做法：

定义E的最大长度为\(maxlen=max(min(i,next_{i},(n-i)/2))(1≤i≤n)\)，然后在\(1\)到\(n-1\)的区间内找一个数字\(i\)，使得\(next_{i}\)最大，且\(next_{i}≤maxlen\)与\(next_{i}+i-1=n\)。

正确性：

我们知道，现在E的长度最长为maxlen（至于为什么，需要读者去深刻理解），\(maxlen\)的作用实际上就是规定了开头的E与中间的E的存在，为寻找最后的E做下铺垫。

\(maxlen\)是怎样的？

\(min(i,next_{i},(n-i)/2))\)实际上是规定了中间的E从\(i\)开始长度最长是多少，中间的\(next_{i}\)就规定了中间的E与开头的E相对成立，在相对成立的情况下，又不能超过\(min(i,(n-i)/2))\)。

那么找到了一个\(next_{i}(next_{i}+i-1=n\) && \(next_{i}≤maxlen)\)时，首先\(next_{i}+i-1=n\)，这规定开头的E与结尾的E，然后\(next_{i}≤maxlen\)，说明这个E的长度没有超过最大的E的限制，将中间的E也规定了，所以这种方法是成立的。

优化：

我们在找\(next_{i}\)的时候，我们可以发现只有在\((2/3)n\)到\(n-1\)里面找才会找到合法的\(next_{i}\)。

我知道我讲的不是很好

我认为讲得挺好的博客

Code

#include<cstdio>
#include<cstring>
#include<algorithm>
#define  N  1100000
using  namespace  std;
int  ne[N],n;
char  st[N];
void  exnext()
{//匹配next数组
    int  b=0,p=0;
    for(int  i=2;i<=n;i++)
    {
        int  L=ne[i-b+1],now=i+L-1;
        if(now<p)ne[i]=L;
        else
        {
            int  qq=p-i+1<0?0:p-i+1;
            while(i+qq<=n  &&  st[qq+1]==st[i+qq])qq++;
            ne[i]=qq;b=i;p=ne[b]+b-1;
        }
    }
}
inline  int  mymin(int  x,int  y){return  x<y?x:y;}//最小值
inline  int  mymax(int  x,int  y){return  x>y?x:y;}//最大值
int  main()
{
    int  T;scanf("%d",&T);
    while(T--)
    {
        scanf("%s",st+1);n=strlen(st+1);
        exnext();
        int  max_len=0;
        for(int  i=1;i<=n;i++)
        {
            int  now=mymin(mymin(i,ne[i]),(n-i)/2);
            max_len=mymax(max_len,now);
        }//处理maxlen
        int  edd=(n*2)/3,ans=0;
        for(int  i=edd;i<=n;i++)//找next[i]
        {
            if(ne[i]>max_len)continue;//不满足条件
            if(i+ne[i]-1==n)//满足条件
            {
                ans=ne[i];//最大的ne
                break;//退出
            }
        }
        printf("%d\n",ans);//输出
    }
    return  0;
}

---

练习二

这道题可以用kmp做，等会说，但是我们讲exkmp的做法。

首先，找到一个长度最短的字符串，一次枚举他的每个后缀与每个字符串匹配到的最小长度，然后取每个前缀得到的值的最大值就行了。

KMP就是枚举前缀，而EXKMP枚举后缀。。。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#define  N  210
using  namespace  std;
inline  int  mymin(int  x,int  y){return  x<y?x:y;}
inline  int  mymax(int  x,int  y){return  x>y?x:y;}
int  ex[N],ne[N]/*就是原本的next数组*/,n,m;
char  st[4100][N];
void  exnext(char  yy[])//匹配出next数组
{
    m=strlen(yy+1);
    int  b=0,p=0;
    for(int  i=2;i<=m;i++)
    {
        int  L=ne[i-b+1],now=i+L-1;
        if(now<p)ne[i]=L;
        else
        {
            int  qq=p-i+1<0?0:p-i+1;
            while(i+qq<=m  &&  yy[i+qq]==yy[qq+1])qq++;
            ne[i]=qq;b=i;p=ne[b]+b-1;
        }
    }
}
int  exkmp(char  xx[],char  yy[])//匹配ne数组
{
    n=strlen(xx+1);//这里不用更新m的原因是在exnext中就更新了m了。
    int  b=0,p=0,maxid=0;
    for(int  i=1;i<=n;i++)
    {
        int  L=ne[i-b+1],now=i+L-1;
        if(now<p)ex[i]=L;
        else
        {
            int  qq=p-i+1<0?0:p-i+1;
            while(i+qq<=n  &&  qq<m  &&  xx[i+qq]==yy[qq+1])qq++;
            ex[i]=qq;b=i;p=ex[b]+b-1;maxid=mymax(maxid,ex[i]);//记录与这个字符串的最大匹配值
        }
    }
    return  maxid;//返回
}
int  main()
{
    int  T,minlen,mind;scanf("%d",&T);
    while(T)//多组数据
    {
        minlen=0;mind=999999999;
        for(int  i=1;i<=T;i++)
        {
            scanf("%s",st[i]+1);
            if(strlen(st[i]+1)<mind)mind=strlen(st[i]+1),minlen=i;
        }//找最短的字符串
        int  ans=0,weizhi=0;
        for(int  i=1;i<=mind;i++)
        {
        	int  now=999999999;//记录最小的匹配值
            exnext(st[minlen]+i-1);//先处理next
            for(int  j=1;j<=T;j++)//找到最小的匹配数
            {
                if(j!=minlen)
                {
                    int  ttk=exkmp(st[j],st[minlen]+i-1);
                    if(ttk<now)now=ttk;
                }
            }
            if(now==ans)//一样的长度？找到最小字典序。
            {
            	for(int  j=1;j<=ans;j++)
            	{
            		if(st[minlen][weizhi+j-1]<st[minlen][i+j-1])break;
            		else  if(st[minlen][weizhi+j-1]>st[minlen][i+j-1]){weizhi=i;break;}
				}
			}
            else  if(now>ans)weizhi=i,ans=now;//最大长度，更新
        }
        if(ans==0)printf("IDENTITY LOST\n");//什么都没匹配到
        else
        {
        	for(int  i=1;i<=ans;i++)printf("%c",st[minlen][weizhi+i-1]);//输出
	        printf("\n");
		}
        scanf("%d",&T);//输入
    }
    return  0;
}

小结

今天终于学会了EXKMP了，先撒一波花。

另外，在码代码的时候需要注意几点：

1. 在不加特判的情况下，\(i-now\)有可能大于\(1\)的。
2. 一开始处理\(next[2]\)和\(ex[1]\)的时候需要注意。

把这几点注意了，基本上你爱怎么打怎么打了。

(:光速逃