KMP模式匹配 学习笔记

功能

能在线性时间内判断字符串\(A[1~N]\)是否为字符串\(B[1~M]\)的子串，并求出字符串\(A\)在字符串\(B\)中各次出现的位置。

实现

1.对字符串\(A\)进行自我“匹配”，求出一个数组\(next\)，其中\(next[i]\)表示“\(A\)中以\(i\)结尾的非前缀子串”与“\(A\)的前缀”能够匹配的最长长度。特别地，当不存在这样的\(j\)时，令\(next[i]=0\).由于\(next\)的对象是非前缀子串，所以\(next[1]=0\)；

概念解释：字符串的前缀是指字符串的任意首部。比如字符串“\(abbc\)”的前缀有“\(a\)”,“\(ab\)”,“\(abb\)”,“\(abbc\)”。同样，字符串的任意尾部是字符串的后缀，“\(abbc\)”的后缀有“\(c\)”,“\(bc\)”,“\(bbc\)”,“\(abbc\)”。

\(next[i]=max{j}，其中j<i并且A[i-j+1~i]=A[1~j]\)

2.对字符串\(A\)与\(B\)进行匹配，求出一个数组\(f\)，其中\(f[i]\)表示“\(B\)中以\(i\)结尾的子串”与“\(A\)的前缀”能够匹配的最长长度。

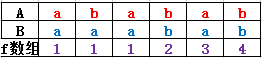
\(f[i]=max{j}，其中j<=i并且B[i-j+1~i]=A[1~j]\)

代码

KMP算法\(next\)数组的求法

1.初始化\(next[1]=j=0\)，假设\(next[1~i-1]\)已求出，下面求解\(next[i]\).

2.不断尝试扩展匹配长度\(j\)，如果扩展失败（下一个字符不相等），令\(j\)变为\(next[j]\)，直至\(j\)为\(0\)（应该从头开始匹配）。

3.如果能够扩展成功，匹配长度\(j\)就增加\(1\).\(next[i]\)的值就是\(j\).

next[1]=0;
for(int i=2,j=0;i<=n;i++)
{
	while(j>0&&&a[i]!=a[j+1]) j=next[j];
	if(a[i]==a[j+1]) j++;
	next[i]=j;
}

KMP算法\(f\)数组的求法

for(int i=1,j=0;i<=m;i++)
{
	while(j>0&&(j==n||b[i]!=a[j+1])) j=next[j];
	if(b[i]==a[j+1]) j++;
	f[i]=j;
	//if(f[i]==n)，此时就是A在B中的某一次出现
}

例题

例题1：P3375 【模板】KMP字符串匹配

这道题完完全全就是对上述两个代码块的直接使用。

#include<iostream>
#include<cstdio>
#include<cstring>
#define N 1000010
#define M 1000010
char p[N],s[M];//p模式串 s主串
int nex[N],f[N];
int ans;
using namespace std;
int main()
{
	cin>>s+1>>p+1;
	int lp=strlen(p+1);
	int ls=strlen(s+1);
	for(int i=2,j=0;i<=lp;i++)
	{
		while(j>0&&p[i]!=p[j+1]) j=nex[j];
		if(p[i]==p[j+1]) j++;
		nex[i]=j;
	}
	for(int i=1,j=0;i<=ls;i++)
	{
		while(j&&(j==lp||s[i]!=p[j+1])) j=nex[j];
		if(s[i]==p[j+1]) j++;
		f[i]=j;
		if(f[i]==lp)
		{
			ans=i-lp+1;
			printf("%d\n",ans);
		}
	}
	for(int i=1;i<=lp;i++) printf("%d ",nex[i]);
	return 0;
}

例题2

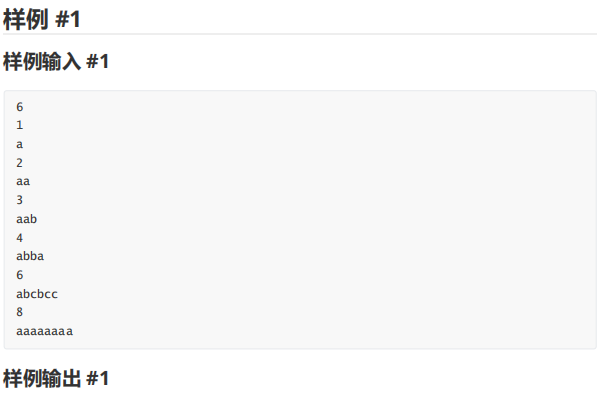
这道题引入了一个新概念：循环同构。

其实，判断两个串是否循环同构也可以利用上述的KMP算法。比如欲判断字符串\(A\)和\(B\)是否循环同构，我们只需要新定义一个字符串\(C\)为重复两遍的\(A\),就是说，若\(A=aab\)，则\(C=aabaab\).然后用KMP判断\(C\)中是否有\(B\)，若有，则\(A\)和\(B\)循环同构，反之则不循环同构。

具体到这道题，我们可以枚举所有因数，然后按因数分段，再用上述方法判断。一旦出现两段之间非循环同构就break,这样能节省不少时间。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=5e6+10;
int t,n;
char a[N];
int nex[N],b[N],f[N];
void kmp(int x)
{
	nex[1]=0;
	for(int i=2,j=0;i<=x;i++)
	{
		while(j>0&&a[i]!=a[j+1]) j=nex[j];
		if(a[i]==a[j+1]) j++;
		nex[i]=j;
	}
}
bool judge()
{
	for(int i=2;i<n;i++)
	{
		if(n%i==0)
		{
			int x=i,p=1,w=n/x;
			bool kx=1;
			kmp(x);
			for(int j=1;j<=w-1;j++)
			{
				for(int k=x*j+1;k<=x*(j+1);k++)
					b[k-x*j]=b[k+x-x*j]=a[k];
				for(int k=1,w=0;k<=x*2;k++)
				{
					while(w>0&&(w==x||b[k]!=a[w+1])) w=nex[w];
					if(b[k]==a[w+1]) w++;
					f[k]=w;
					if(f[k]==x)
					{
						kx=1;
						p++;
						break;
					}
					kx=0;
				}
				if(!kx) break;
			}
			if(p==w) return 1;
		}
	}
	for(int j=1;j<n;j++)
		if(a[j]!=a[j+1])
			return 0;
	return 1;
}
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d%s",&n,a+1);
		if(n==1)
		{
			puts("No");
			continue;
		}
		if(judge()) puts("Yes");
		else puts("No");
	}
	return 0;
}