代码随想录训练营day 1 |704 二分查找 27移除算法

LeetCode 704.二分查找（C++）

题目链接 704.二分查找

题目描述：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

思路：

二分法经常会写错，这是因为对区间的定义没有想清楚，区间的定义就是不变量？？一般分为两种区间，一种是左闭右闭，一种是左闭右开。
一般就是对到底是 while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？这里搞不清楚。

第一种写法（左闭右闭）

定义target是在一个左闭右闭的区间里，即：[left,right].

那么while（）里面就应该是left <= right,因为此时right是可以取到值的，所以要加上等于号。

if (nums[middle] > target) 这里意思是中间值大于了目标值，所以要在区间前面去找，而

之前已经是[left,right]，而且nums【mid】一定不是target，所以左边区间还是[left,右边区间就应该是mid-1=right],不减一的话就会取到mid值就不精确了。

代码如下：（加注释）

    class Solution {
public:
int search(vector<int>& nums, int target) {//vector类似数组但比数组吊
    int left =0;
    int right =nums.size()-1;//right为最右边，这里的nums.size()名为nums的对象的size成员函数，类比size为8，但是最后下标为7。//
    while (left <=right){//left==right是依然有效
        int middle=left+((right-left)/2);//防止溢出，left right middle均为下标值,其实就是等同于（left+right）/2
        if(nums[middle]>target){//mid大于目标值，则要去左区间查找
            right=middle-1;        //同上，[left,middle-1]
        }
        else if(nums[middle]<target){//mid小于目标值，则要去右区间查找
            left=middle+1;       //这里同上（因为mid不等target且左百边可取等号），所以[middle+_1,right]
        }
        else{ // nums[middle] == target
            return middle;   //target==mums[middle]，输出下标值
        }
    }
    return-1;//未找到目标值
    }
};

第二种写法（左闭右开）

也就是[left, right) ，那么二分法的边界处理方式则截然不同。

有如下两点：

一、while (left < right)，这里使用 < ,因为left == right在区间[left, right)是照样取不到right的

二、if (nums[middle] > target) ，这里的mid大于目标值则要去左边找，所以要动right的值，right 更新为 middle，因为当前nums[middle]不等于target，例如{1，8）实际范围是{1，7}，所以可以等于mid。

代码如下（带注释）

class Solution {
public:
int search(vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
    while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
        int middle = left + ((right - left) >> 1);
        if (nums[middle] > target) {
            right = middle; // target 在左区间，在[left, middle)中
        } else if (nums[middle] < target) {
            left = middle + 1; // target 在右区间，在[middle + 1, right)中
        } else { // nums[middle] == target
            return middle; // 数组中找到目标值，直接返回下标
        }
    }
    // 未找到目标值
    return -1;
  }
};

LeetCode 27. 移除元素(C++)

题目链接：27. 移除元素

题目描述：示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。

示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。

思路：

要知道数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。不能直接删除就完事了，删了一个元素必须要让后面的全部往前补上。
那么暴力算法可以解决这个问题，但是复杂度有待商榷。其次就是双指针法解题。

暴力算法

这个题目暴力的解法就是两层for循环，一个for循环遍历数组元素 ，第二个for循环更新数组。

暴力解法的时间复杂度是O(n^2)，这道题目暴力解法在leetcode上是可以过的。

这道题要那笔多演算几遍好理解一点。

代码如下：

// 时间复杂度：O(n^2)
// 空间复杂度：O(1)
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
    int size = nums.size();
    for (int i = 0; i < size; i++) {//for循环 一般是1 2 4 3的形式进行循环，1是定义，2是条件，3是循环体，4是表达式。
        if (nums[i] == val) { // 发现需要移除的元素，就将数组集体向前移动一位
            for (int j = i + 1; j < size; j++) {//i
                nums[j - 1] = nums[j];
            }
            i--; // 因为下标i以后的数值都向前移动了一位，所以i也向前移动一位
            size--; // 此时数组的大小-1
        }
    }
    return size; 

}
};

单向双指针法

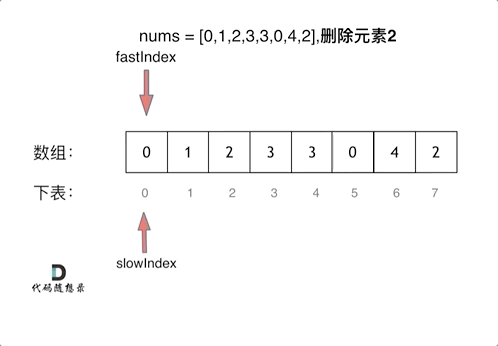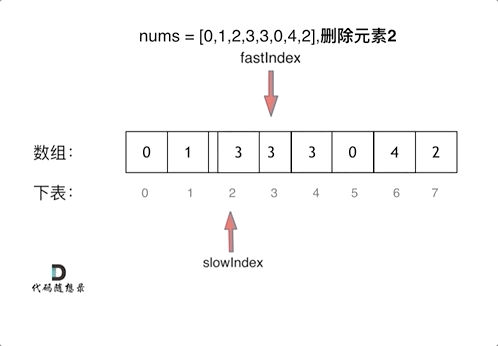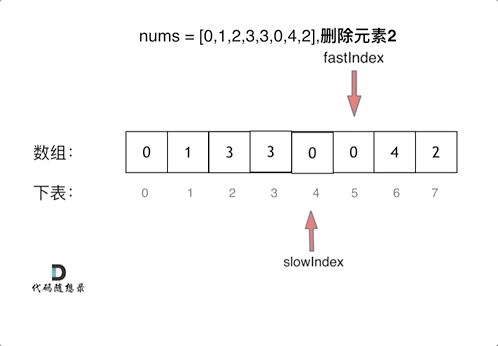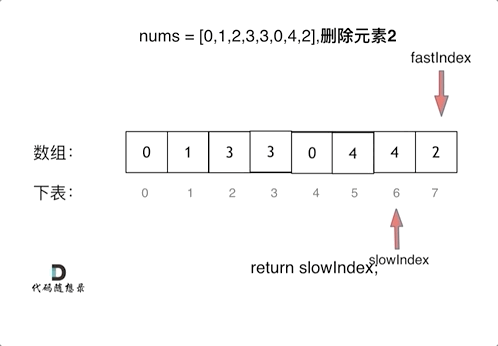
（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

定义快慢指针：

快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组//寻找新数组的元素，即将需删除的元素跳过后的新数组

慢指针：指向更新 新数组下标的位置

代码如下：代码看着简单，但是细节很多，挺难理解，动手走一遍就很舒服。

详细看卡哥视频：妙解二分法

// 时间复杂度：O(n)
// 空间复杂度：O(1)
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
    int slowIndex = 0;
    for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
        if (val != nums[fastIndex]) {//目标值不等于fast，就要拿去做新数组
            nums[slowIndex++] = nums[fastIndex];//也可是：nums[slowIndex] = nums[fastIndex]; lowIndex++;
        }
    }
    return slowIndex;
}
};

总结

① middle=left+(right-left)/2等同于(left+right)/2，可以防止溢出。原因：当left和right足够大时，left+right后可能导致结果超出范围，如果使用left+(right-left)/2则可以保证middle始终在left和right之间。right-left必定小于数组范围。

② left一定是middle+1，因为middle已经确定≠target，所以要加一进行区间判断。

由于是左闭右开，middle<target即可保证判断区间时不会含上middle，所以right=middle即可，左闭右闭区间需要right=middle-1

③ 相向双指针方法，基于元素顺序可以改变的题目描述改变了元素相对位置，确保了移动最少元素，二刷时注意写一遍。