angr原理与实践（二）—— 各类图的生成（CFG CG ACFG DDG等）

​

 本文系原创，转载请说明出处

Please Subscribe Wechat Official Account：信安科研人，获取更多的原创安全资讯

上一篇文章介绍了angr的原理，自此篇文章开始，将从一个个小实验的角度，讲述队angr的一些用法。

第二篇从（静态）程序分析必备的基础元素的角度出发，介绍一些图的生成与应用。

一 CFG（控制流图）与CG（调用图）

---

1.1 CFG控制流图：

概念：控制流图（control-flow graph）简称CFG，是计算机科学中的表示法，利用数学中图的表示方式，标示计算机程序执行过程中所经过的所有路径。控制流图是由法兰·艾伦所建立，他提出Reese T. Prosser（英语：Reese Prosser）曾利用邻接矩阵用在流分析上。

性质：

• 节点基本块，内含程序语句；基本块概念基本块 - 维基百科，自由的百科全书 (wikipedia.org)
• 边代表控制流，即如何执行

​特征：

• 面向过程
• 显示程序执行期间可以遍历的所有路径
• 有向图

优点：

        可以轻松封装每个基本块的信息

可以轻松找到程序中无法访问的代码，并且在控制流图中很容易找到循环等语法结构

缺点：

只能表示控制依赖关系，数据依赖关系表示能力较弱

使用angr生成CFG的示例代码：

在第一篇文章中提到angr实现生成CFG的几种算法，方法按结果可以分为：CFGFast()， CFGEmulated。

使用流程一般为：

1. 加载文件
2. 调用图方法               

angr调用方法：

import angr
from angrutils import *

p = angr.Project(程序路径)

#使用快速生成方法生成CFG
cfg = p.analyses.CFGFast()

#使用完整生成方法生成CFG
cfg1 = p.analyses.CFGEmulated()

#调用angr-utils库可视化
plot_cfg(cfg1, "生成的cfg文件名", asminst=True, remove_imports=True, remove_path_terminator=True)  

示例：

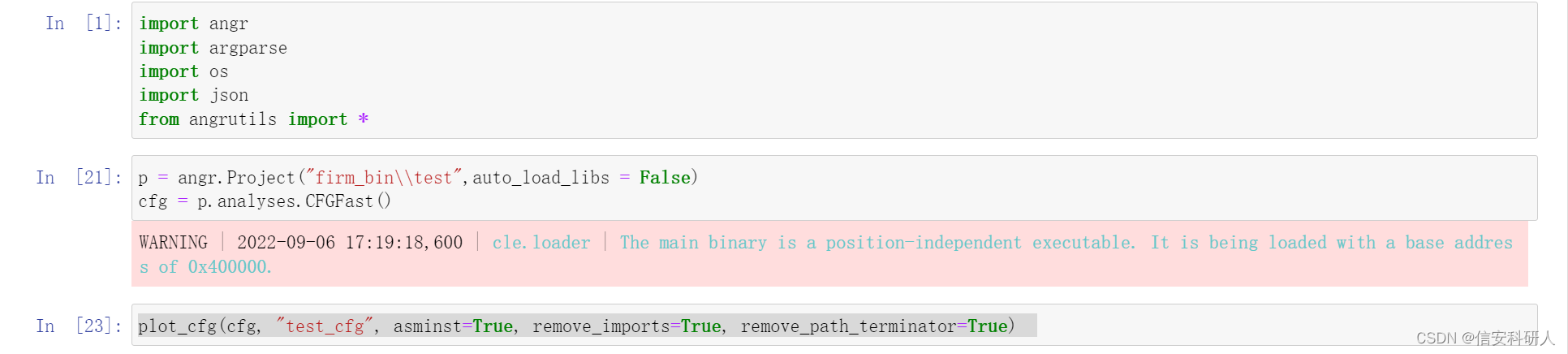
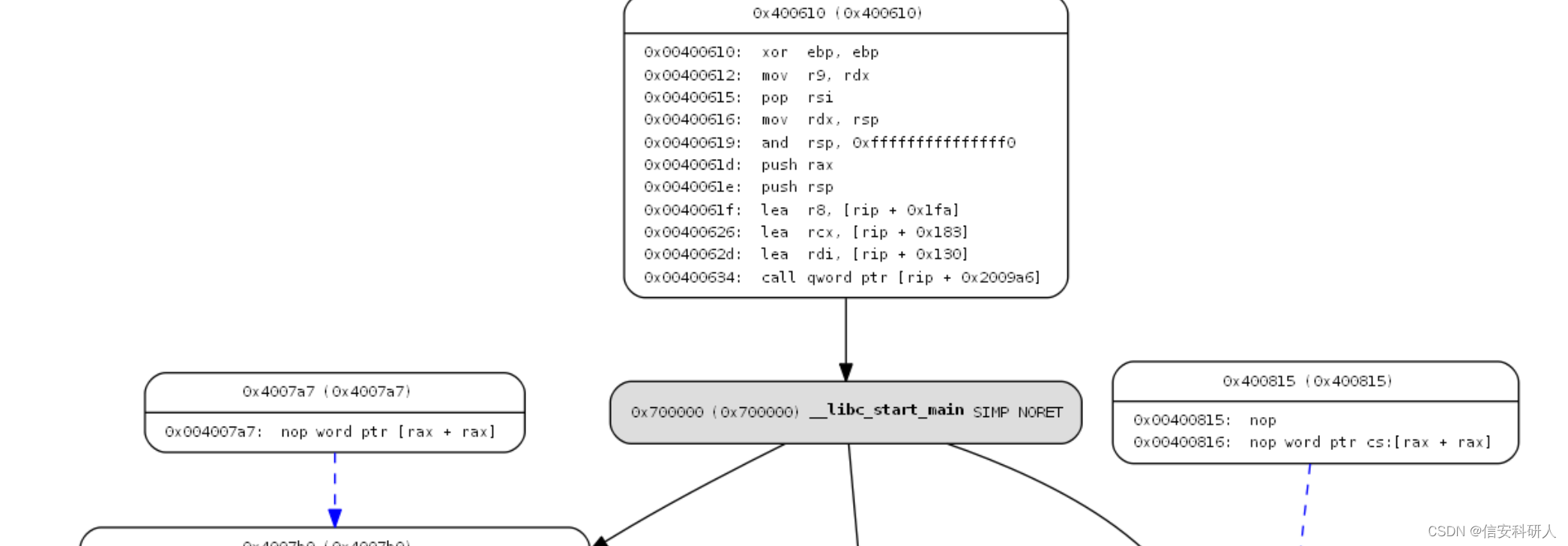
​编辑

​

编辑

1.2 CG 调用图

概念：一种有向图，表示计算机程序中调用和调用子例程之间的关系，用于代码分析。每个节点表示一个过程，每个边 （f， g） 表示过程 f 调用过程 g。

特点：

两种CG，一种是动态，一种是静态

静态：静态调用图是用于表示程序的每个可能运行的调用图。确切的静态调用图是一个不可判定的问题，因此静态调用图算法通常是过度的。也就是说，发生的每个调用关系都表示在图中，并且可能还有一些在程序的实际运行中永远不会发生的调用关系。

动态：动态调用图只描述程序的一次运行

代码示例：

angr里比较常见的是函数的CG，需要注意区分概念

p = angr.Project(文件路径)
cfg = p.analyses.CFGFast()
cg = cfg.functions.callgraph
#cg即是函数调用图

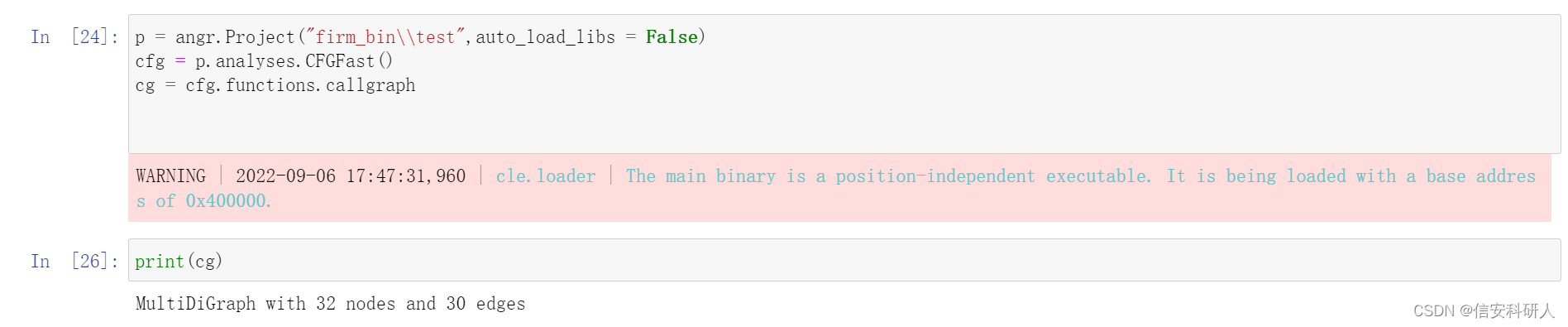
​编辑

二 CDG和DDG （依赖图类，后续更新PDG、CPG）

---

依赖图一般是在CFG的基础上，按照特定的分析需求，构建特定的依赖图。常见的依赖图类包含CDG、DDG、CPG、PDG。angr按照自带的后向切片方法，在CFG上构建了生成CDG和DDG的方法，另外两种需要重构。

CDG（控制流依赖图）

概念：

人话定义：对于CFG中的两个节点X和Y，如果Y受X控制，即如果在程序执行过程中，X能直接影响Y是否执行

规范定义：

• 对于一个有向图 G = < N , E >，节点n控制依赖于节点m，当且仅当：
• 存在一条m到n的控制路径，n是该路径上除m之外每个节点的后支配节点，并且n不是m的后支配节点。

本文参考这边博文，即CDG由CFG和FDT(前向支配树构成)，d支配（dominate）n，记为d dom n：每一条从流图的入口结点到结点n的路径都经过结点d 。在这个定义下每个结点都支配它自己
如下图所示，左侧为流图，右侧为其对应的支配树

​

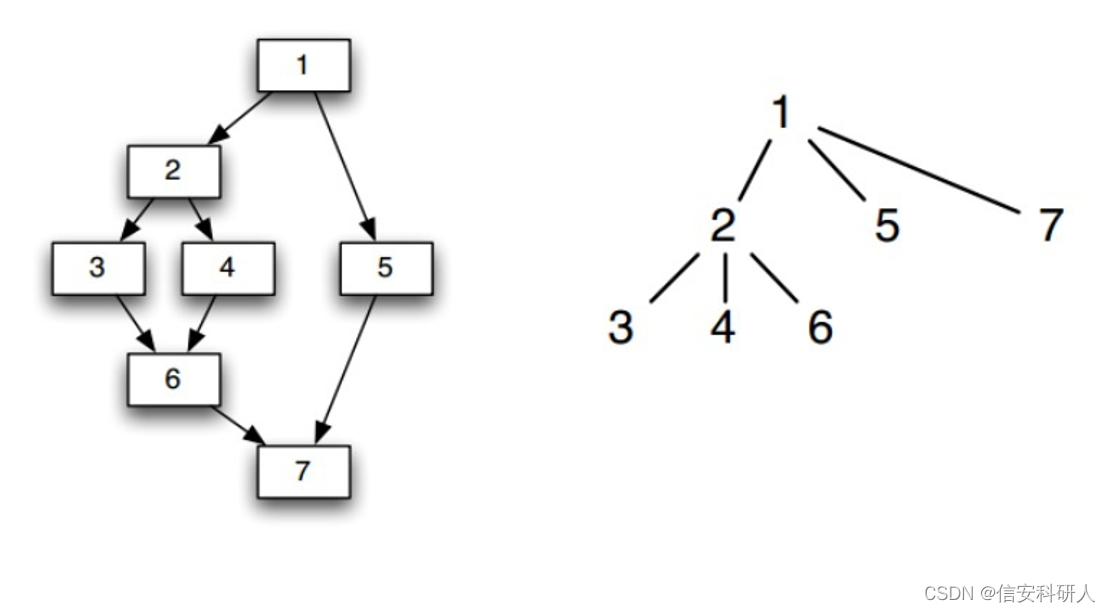
编辑

简单的来说如何划分，即如果现在这个节点只有一条入边，那么逆着入边往上看第一个节点直接控制现在这个节点，如2和3；如果现在这个节点有多条入边，逆着入边往上看，以一种合并的方式，找到这些入边往上合并的第一个节点，就是直接控制现在这个节点的节点。

又如如下例子：第一张图是程序示例和对应的CFG，第二张图是CDG和变量X的DDG

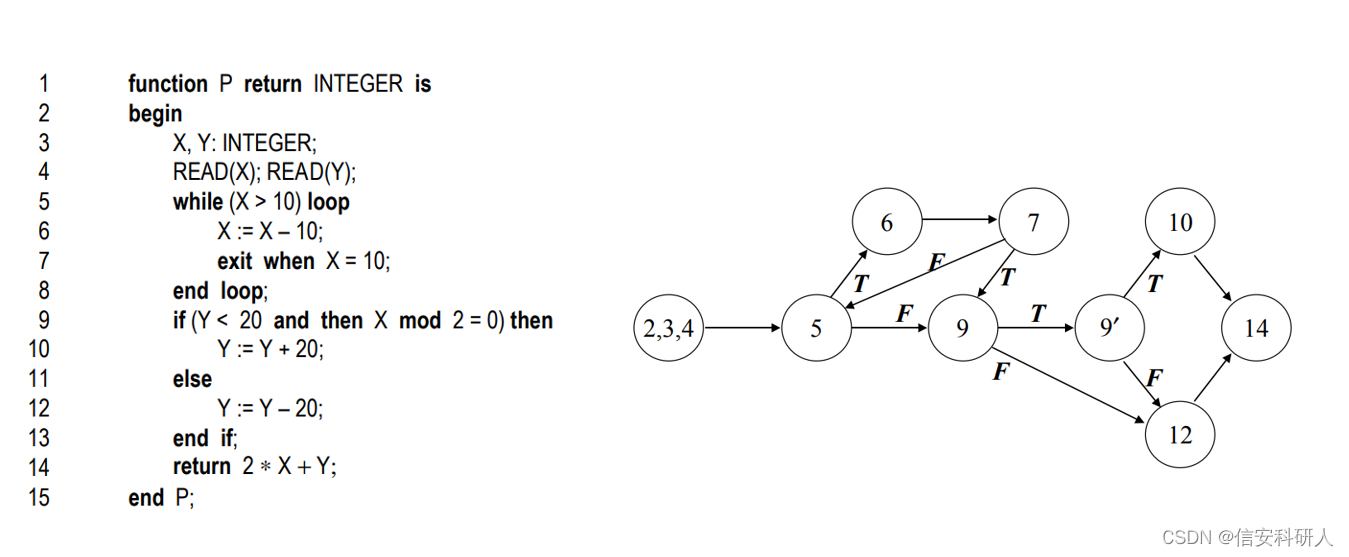
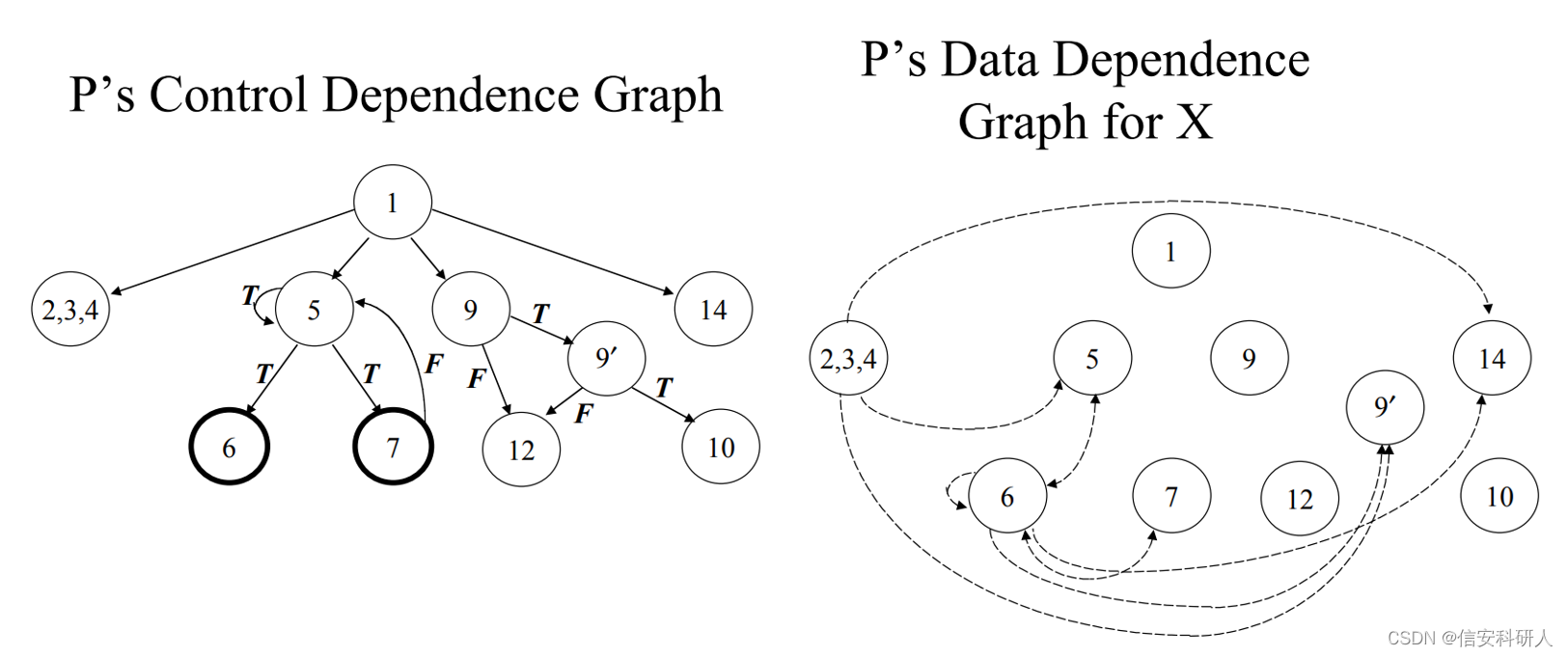
​编辑

​编辑

应用：

死代码删除（DCE，Dead Code Elimination）和激进死代码删除（ADCE，Aggressive Dead Code Elimination）是编译中常见的优化pass。相较于DCE，ADCE会删除冗余的分支。

示例代码

import angr

b = angr.Project(文件路径)

cfg = b.analyses.CFGEmulated(keep_state=True,
                           state_add_options=angr.sim_options.refs,
                            context_sensitivity_level=2)

# 生成控制流依赖图
cdg = b.analyses.CDG(cfg)

DDG (数据依赖图)

定义：

• 两个句子存在数据依赖：一条语句中一个变量的定义，可以到达另一条语句中对该变量的使用
• 在编译领域有不同类型的数据依赖，如果s2依赖于s1，可以是：
  1. s1 写内存 s2 读 (RAW)
  2. s1 读内存 s2 写 (WAR)
  3. s1 写内存 s2 写 (WAW)
  4. s1 读内存 s2 读 (RAR)
• 如果两个语句可能引用相同的内存位置和引用之一，则它们是数据相关的

代码示例：

import angr

b = angr.Project(文件路径)

cfg = b.analyses.CFGEmulated(keep_state=True,
                           state_add_options=angr.sim_options.refs,
                            context_sensitivity_level=2)

# 生成数据流依赖图
ddg = b.analyses.DDG(cfg)

ACFG 属性控制流图

---

在很多代码相似性检测的工作中，常常需要二进制程序的结构和语义信息，ACFG诞生于二进制程序漏洞检测的工作GENIUS中，其定义了ACFG属性控制流图，以获取二进制程序的基本块的内部特征，以及外部的结构特征，从而将其嵌入向量空间，使用机器学习按照代码相似性的技术，进行漏洞检测。

Scalable Graph-based Bug Search for Firmware Images | Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security

定义：

一个有向图G = <V,E,α>，V为基本块集合，E是边集合，α代表基本块的特征标签集合，一般定义特征集合如下（参考此博文）

​编辑

最后形成的ACFG如下：

​

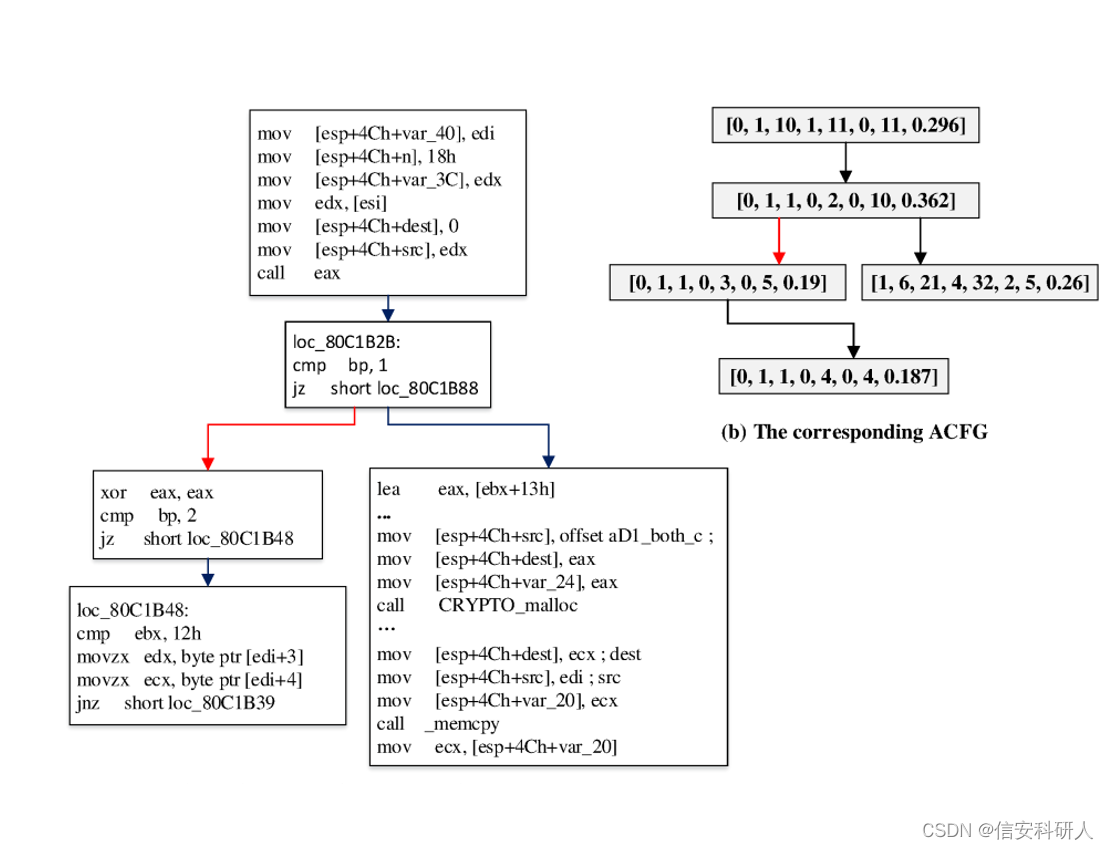
编辑

代码示例：

首先导入库函数

import angr
import argparse
import os
import json
from angrutils import *

接着，从基本块中获取指令的统计特征，指令的种类需要手工枚举，数量有限，问题不大：

def calc_ins(insns):
    """
    统计基本块中指令类型的数量
    参数insns为angr调用cfg中的基本块
    """
    transfer_ins = ['MOV', 'PUSH', 'POP', 'XCHG', 'IN', 'OUT', 'XLAT', 'LEA', 'LDS', 'LES', 'LAHF', 'SAHF', 'PUSHF','POPF']

    arithmetic_ins = ['ADD', 'SUB', 'MUL', 'DIV', 'XOR', 'INC', 'DEC', 'IMUL', 'IDIV','OR', 'NOT', 'SLL', 'SRL']

    calls_ins = ['CALL']

    num_transfer = 0
    num_arithmetic = 0
    num_calls = 0

    for ins in insns:
        ins_name = ins.insn_name()   #angr基本块中的block.capstone.insns.insn_name()方法

        if ins_name in transfer_ins:
            num_transfer = num_transfer + 1

        if ins_name in arithmetic_ins:
            num_arithmetic = num_arithmetic + 1

        if ins_name in calls_ins:
            num_calls = num_calls + 1

    return num_transfer, num_calls, num_arithmetic

然后，获取基本块的其他特征，如字符串常量的个数、数值常量的个数、指令总数：

def calc_block(block, num_str):
    """
    统计每个基本的特征
    """
    # 字符串常量个数初始化，通过传入外部的angr字符串个数计数方法
    num_string = num_str

    # 数字常量的个数
    num_numeric = len(block.vex.constants)

    # 指令的总数
    num_instructions = block.instructions

    # 指令集区分并计数
    num_transfer, num_calls, num_arithmetic = handle_ins(block.capstone.insns)

    # 基本块子节点个数
    num_offspring = 0

    return [num_string, num_numeric, num_transfer, num_calls, num_instructions, num_arithmetic, num_offspring]

接着，在定义好统计基本块内部的特征后，以一个函数为单位，统计基本块的外部结构特征，如连接的节点个数，子节点个数，使用邻接矩阵记录这些节点关系：

def calc_function(function, func_addr):
    """
    提取每个函数的特征
    """

    function_feature = dict()
    function_feature["func_addr"] = func_addr       #函数的位置
    function_feature["function_name"] = function.name  #函数名
    function_feature["features"] = []     #函数内基本块的总特征
    function_feature["adj"] = []        #函数内的基本块结构

    try:
        # 函数中字符串常量的个数
        f_num_string = len(function.string_references())
        block_cnt = 0   

        # 提取函数内每个基本块的属性并统计基本块的个数
        for blk in function.blocks:
            function_feature["features"].append(calc_block(blk, f_num_string))
            block_cnt = block_cnt + 1
        function_feature["block"] = block_cnt

        # CFG图的节点数目为0时直接返回
        if 0 == len(function.graph):
            return

        # 将函数中的基本块结构图转为邻接矩阵
        matrix = nx.adjacency_matrix(function.graph).todense().tolist()

        for i, line in enumerate(matrix):
            # 当前节点到自己无边
            line[i] = 0
            num_offspring = line.count(1) #计算子节点个数

            function_feature["features"][i][-1] = num_offspring
            function_feature["adj"].append(line)

        print("*************************************")
        print(function_feature)

    except Exception as e:
        print("Exception->", e)

这里比较难理解的操作是邻接矩阵这块，把它打印出来看会更容易理解：

​

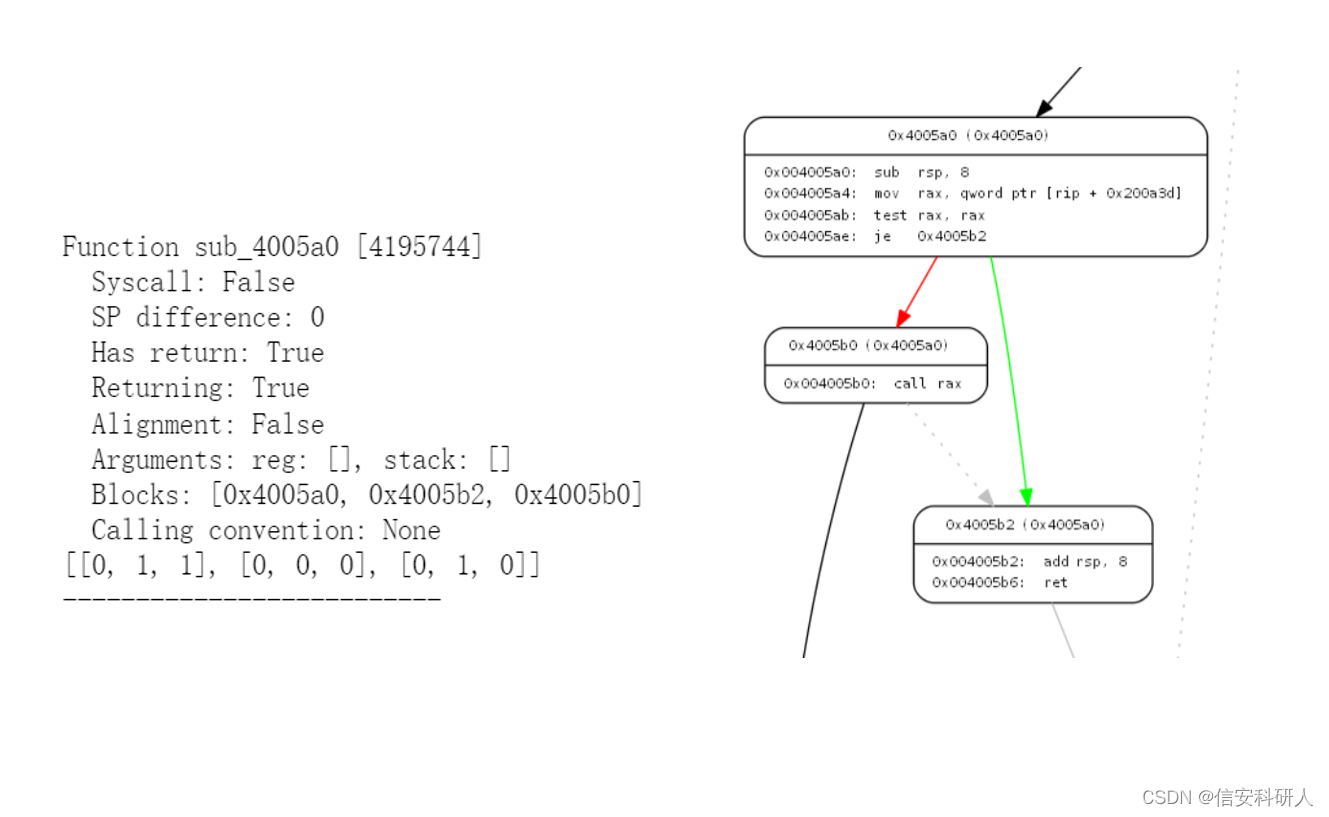
编辑

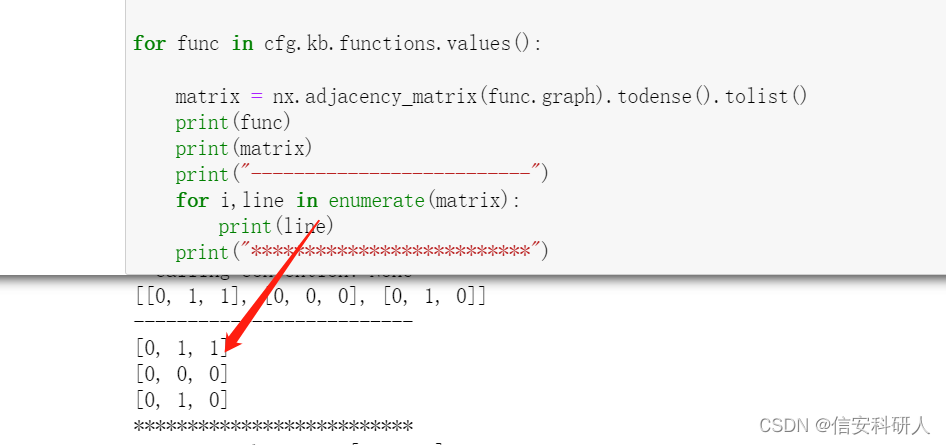
上左图是一个函数的具体信息和邻接矩阵（最后一行），右图是可视化CFG后该函数对应的部分，可以看到0x4005a0基本块节点到本身无边，因此为0，到第二个0x4005a0和第三个0x4005b0都有边，所以，最后为[0,1,1]；第二个[0,0,0]按顺序为0x4005b2基本块，可以看到，其到其他两个都没有指向边，因此全为0；最后一个同理。

所以，对于每个line，如下图，就是一个基本块的节点连接情况，计算line.count(1)就是计算子节点的个数

​

编辑

最后，对每个文件进行方法调用即可：

​编辑

​