stata基础（十五）——线性回归的基本假定、估计回归系数、拟合系数

一、回归：回归是研究变量间相互关系的方法

1、条件分布：因变量在自变量取不同值时的分布

如果因变量在自变量取不同值时的条件分布都相同，那么自变量对因变量没有影响，否则就是有影响。

比较因变量在自变量取不同值时的条件分布过于复杂，一个简化方法就是

比较自变量取不同值时因变量条件分布的均值——回归

E(y|x) = f(x)

2.线性回归：用线性函数来描述自变量与因变量条件均值的一种回归方法。

3.四条基本假定：最重要的是前2条假定，一旦不满足会导致估计结果有偏。——一定要保证函数设定正确，确保不要遗漏关键变量

（1）线性假定：y的条件均值为x的线性函数：E(y|x) = b₀+b₁x₁+b₂x₂+...+b_kx_k

非线性关系可以通过非线性变换转变成线性

（2）正交假定：

（3）独立同分布假定：不满足会导致估计结果没有效率，但仍是无偏的。可以使用其他估计方法（如：OLS）获得有效估计值，或使用稳健标准误获得正确的统计检验结果。

①同方差假定：

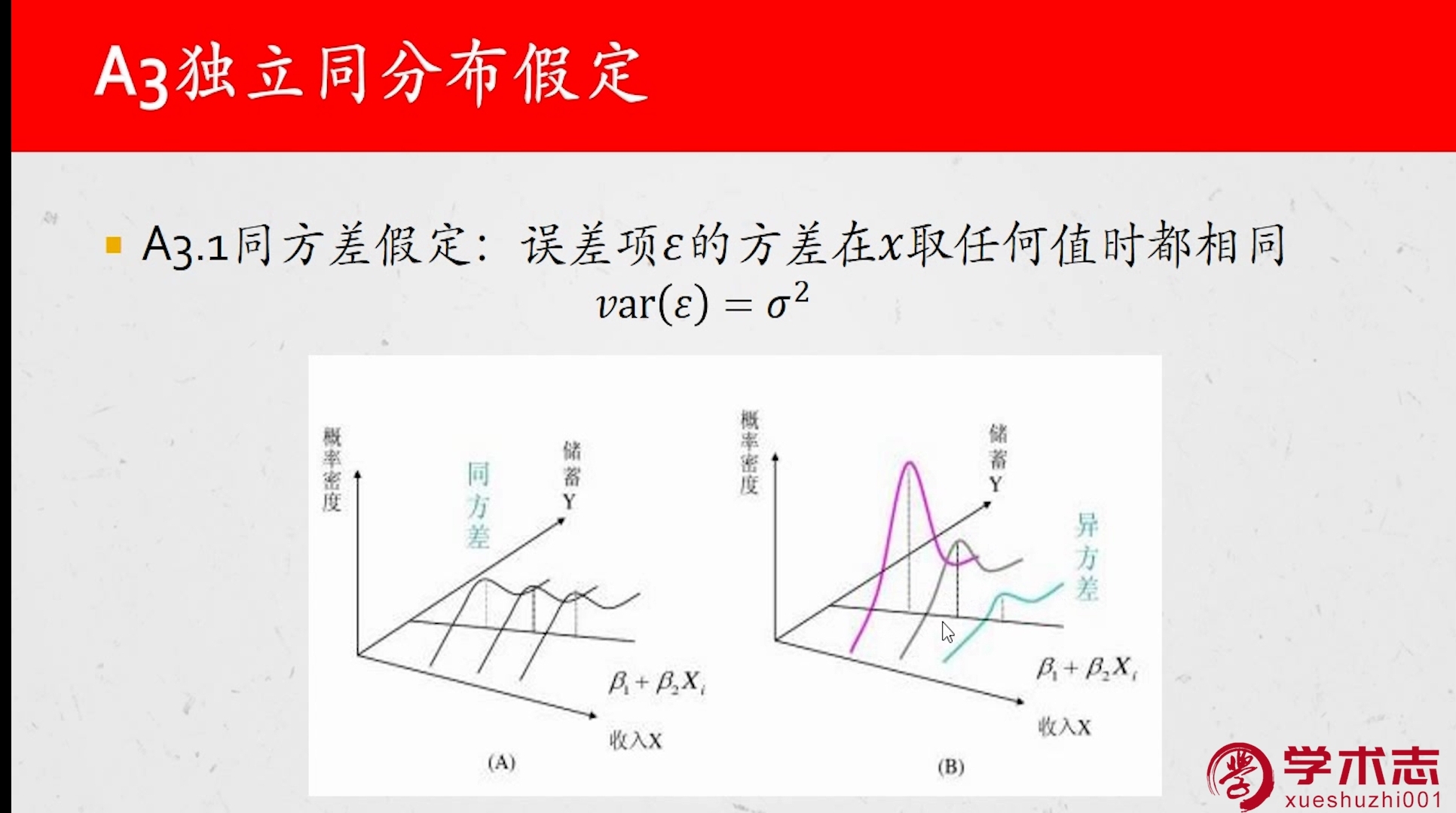
②无自相关：

常见的存在自相关的情形：

A.时间序列：同一个观测对象在不同时点得到的结果。

B.整群抽样

（4）正态分布假定：在小样本使才是必须的，否则无法进行统计检验，但大样本时不需要（中心极限定理）

4.回归假定的意义：满足上述假定，通过普通最小二乘法（OLS）得到的回归估计值将有很好的统计性质

（1）满足A1和A2，可以保证OLS估计值的无偏性（样本回归系数=总体均值）；

（2）满足A1、A2和A3，可以保证BLUE（最优线性无偏估计——效率最高，标准误最小）；

（3）满足A1、A2、A3和A4，可以保证BUE（最优无偏估计）。

回归假定如果不满足，依然可以求解，只是估计值将不具有上述性质。

二、估计回归系数

1.方法：

（1）最小二乘法：寻找一组回归系数使残差平方和最小

（2）最大似然法：寻找一组回归系数使样本结果出现的概率最大

可以证明，这两种方法得到的系数估计值是等价的。

2.regress命令：regress depvar [indepvars] [if] [in] [weight] [,options]

regress后先写因变量，再写自变量

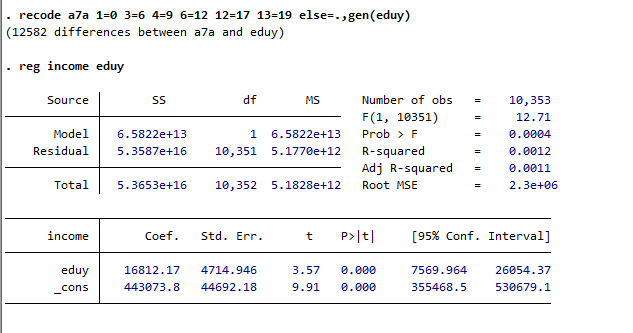
一元回归：

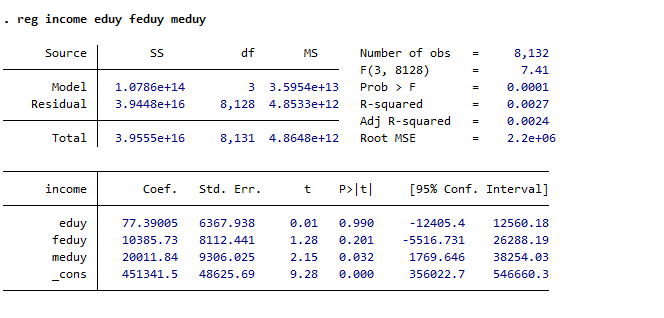
多元回归：

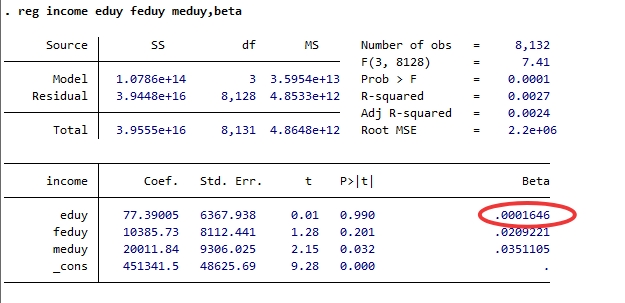
标准化回归系数：

按上述公式手动检验结果：

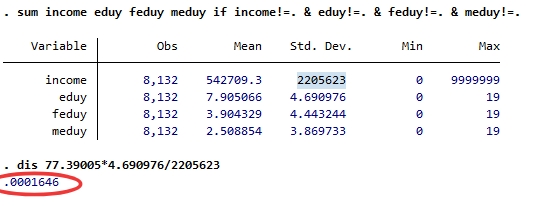
综上，

非标准化回归系数：stata默认输出的结果。解释为在控制其他变量的情况下，自变量x_j变化1个单位，y变化b_j个单位。

标准化回归系数：须使用选项beta。解释为在控制其他变量的情况下，自变量x_j变化1个标准差，y变化beta_j个标准差。

标准化回归系数消除了自变量和因变量测量单位的影响，所以可以比较不同自变量对因变量的相对影响大小

但是，由于不同总体中自变量和因变量的标准差不同，所以无法跨样本比较beta_j。

三、拟合系数——R²

1.确定系数 R²：因变量y的残差平方和中被自变量解释掉的百分比

R² = RSS/TSS

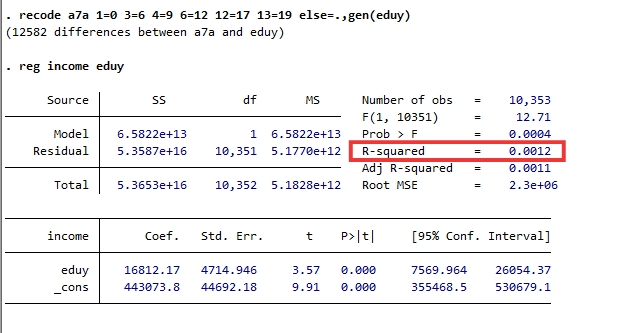
2.R²的意义

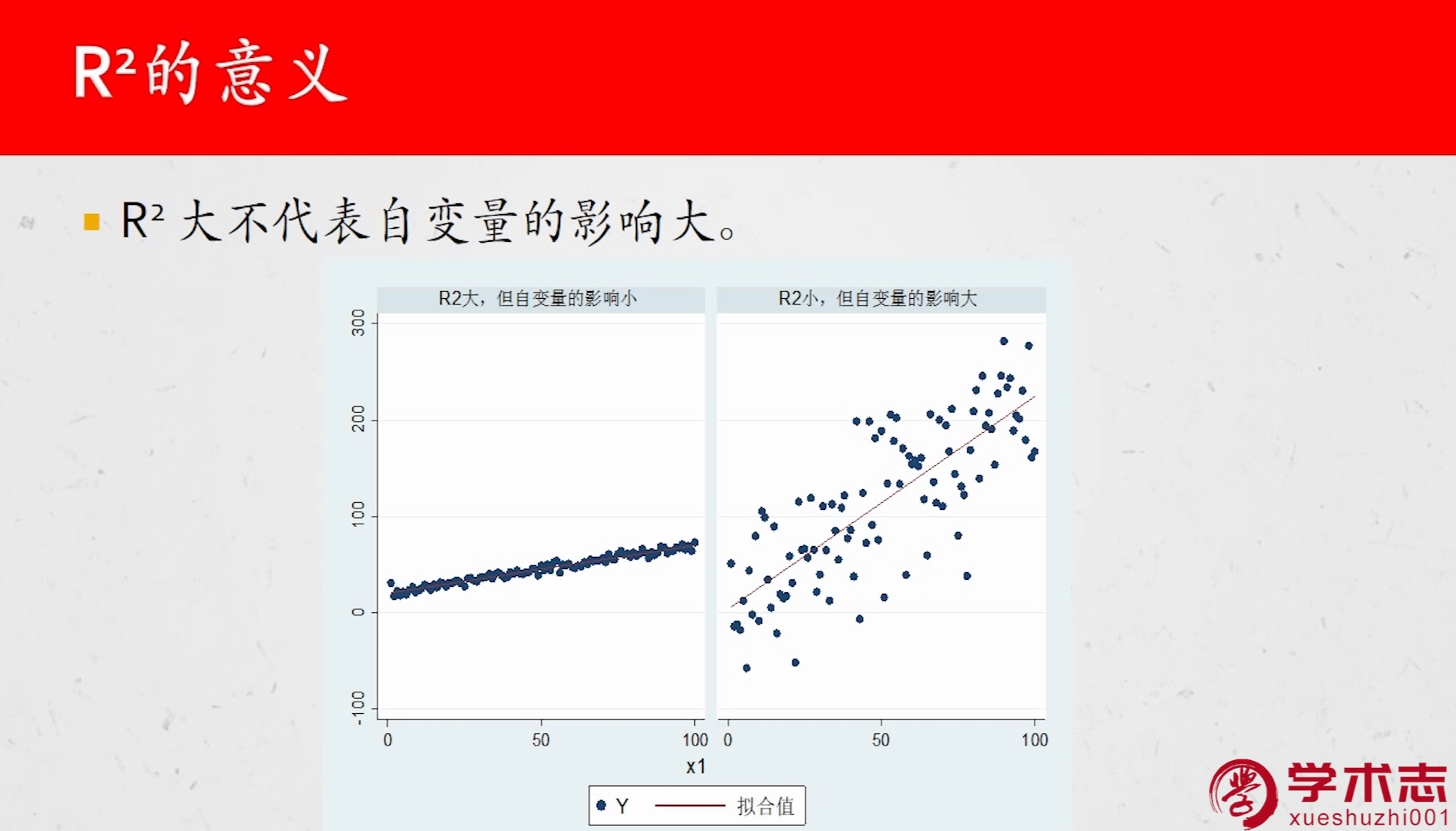
斜率大的模型，自变量的影响大；斜率小的模型，自变量影响小。

R²越大，模型对数据的拟合效果越好，但R²并不是越大越好

例：“布劳-邓肯”地位获得模型：美国的家庭背景对子女地位获得的影响——R²越大，说明家庭背景对子女地位获得的影响越大，说明是一个等级森严、难以跨越的社会；反之，家庭背景对子女地位获得的影响较小，则说明社会较为平等和人才流动。因此，不仅要看R²的统计学意义，还要看所研究的问题的社会学含义

多大的R²可以接受取决于研究的目标：

①如果回归分析的目标是预测，那么R²越大预测越准确、越好；

②如果回归分析的目标是获得某自变量对因变量的真实影响（关键在于模型的假定是否满足），R²是大是小关系并不大。

3.R²的缺陷：随着自变量的增加，R²也会随之增加，无论该自变量对因变量是否有影响

改进：在原始R²的基础上，对自变量数量进行惩罚（Adj R-squared）

——调整后的缺陷：调整后的R²缓解了原始R²的上述缺陷，但它的理论意义并没有原始的R²那么直接

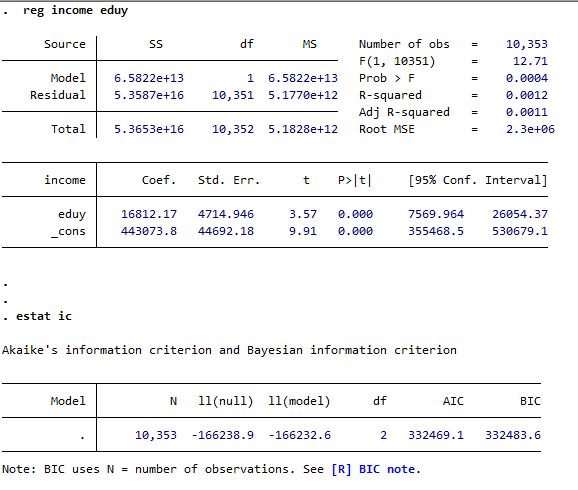
4.其他拟合指标

一些学者认为，调整后的R²对复杂模型的惩罚不够大，因此提出了AIC和BIC两个模型拟合指标

命令：在运行regress后使用estat ic命令可输出AIC和BIC，这两个指标与R²相同，用于判断拟合优度，但AIC和BIC越小，拟合程度越好。

estat ic命令是回归分析后的一种估算命令