论文解读《Deep Attention-guided Graph Clustering with Dual Self-supervision》

论文信息

论文标题：Deep Attention-guided Graph Clustering with Dual Self-supervision
论文作者：Zhihao Peng, Hui Liu, Yuheng Jia, Junhui Hou
论文来源：2022, arXiv
论文地址：download
论文代码：download

1 Introduction

　　当前考虑拓扑结构信息和语义信息的深度聚类方法存在的问题：

• • 将 DAE 和 GCN 提取到的特征重要性同等看待；　　
  • 忽略了不同层次的多尺度信息；　　
  • 没有充分利用从 cluster 中的可用信息；　　

2 Method

　　总体框架：

　　

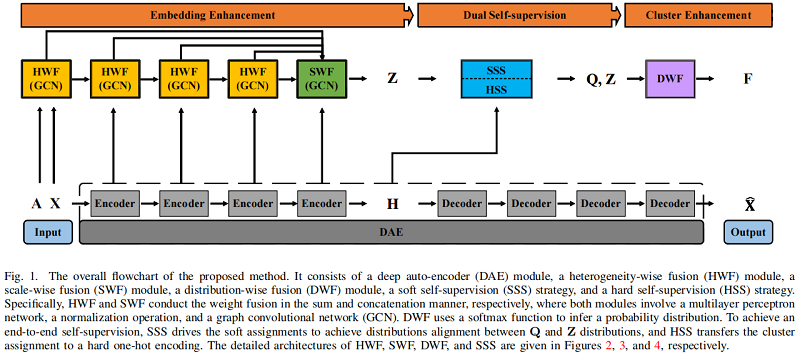
　　组成部分：

• • a heterogeneity-wise fusion (HWF) module　　
  • a scale-wise fusion (SWF) module　　
  • a distribution-wise fusion (DWF) module　　
  • a soft self-supervision (SSS) strategy　　
  • a hard self-supervision (HSS) strategy　　

　　由于聚类任务没有真实标签作为监督信息，所以采用 Student’s t-distribution $Q$ 用来度量特征 $\mathbf{h}_{i}$ 和其质心 $\boldsymbol{\mu}_{j}$ 的相似性：

　　　　${\large q_{i, j}=\frac{\left(1+\left\|\mathbf{h}_{i}-\boldsymbol{\mu}_{j}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}}{\sum\limits _{j^{\prime}}\left(1+\left\|\mathbf{h}_{i}-\boldsymbol{\mu}_{j^{\prime}}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}} }  \quad\quad\quad(1)$

　　为了进一步提高置信度，求目标分布 $B$：

　　　　${\large b_{i, j}=\frac{q_{i, j}^{2} / \sum\limits _{i} q_{i, j}}{\sum\limits _{j}^{\prime} q_{i, j}^{2} / \sum\limits _{i} q_{i, j}^{\prime}}}    $

　　然后最小化两个分布之间的距离：

　　　　$\min K L(\mathbf{B}, \mathbf{Q})=\sum\limits _{i} \sum\limits _{j} b_{i, j} \log \frac{b_{i, j}}{q_{i, j}}  \quad\quad\quad(2)$

2.1 （HWF）Heterogeneity-wise Fusion module

　　深度自动编码器(DAE)和图卷积网络(GCN)可以分别提取节点内容特征和拓扑结构特征。然而，以往的研究将从DAE和GCN中提取的特征的重要性等同起来，这在一定程度上是不合理的。为此，如 Figure 2 的左边界所示，我们提出了一个异构融合(HWF)模块来自适应地集成DAE和GCN特征，以学习区分特征嵌入。

　　

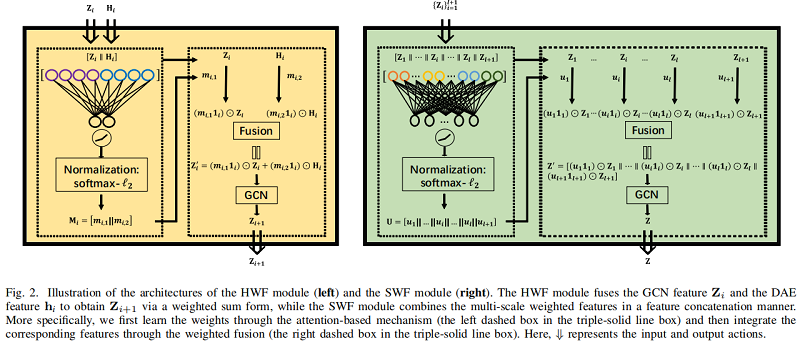
　　利用深度自编码器（DAE）提取潜在表示，重构损失如下：

　　　　$\begin{array}{l}\mathcal{L}_{R}=\|\mathrm{X}-\hat{\mathrm{X}}\|_{F}^{2} \\\text { s.t. } \quad\left\{\mathrm{H}_{i}=\phi\left(\mathrm{W}_{i}^{\mathrm{e}} \mathrm{H}_{i-1}+\mathrm{b}_{i}^{\mathrm{e}}\right)\right. \\\left.\hat{\mathrm{H}}_{i}=\phi\left(\mathrm{W}_{i}^{d} \hat{\mathrm{H}}_{i-1}+\mathrm{b}_{i}^{d}\right), i=1, \cdots, l\right\}\end{array}\quad \quad \quad (3)$

　　其中：

• • $\mathrm{X} \in \mathbb{R}^{n \times d}$ 代表了原始数据（raw data）；　　
  • $\hat{\mathrm{X}} \in \mathbb{R}^{n \times d}$ 代表了重构数据（ reconstructed data）；　　
  • $\mathrm{H}_{i} \in \mathbb{R}^{n \times d_{i}}$ 代表了 Encoder 第 $i$ 层的输出；　　
  • $\hat{\mathrm{H}}_{i} \in \mathbb{R}^{n \times \hat{d}_{i}}$ 代表了 Decoder 第 $i$ 层的输出；　　
  • $\phi(\cdot)$ 代表了激活函数，如 Tanh, ReLU ；　　　　
  • $W _{i}^{e}$ 和 $b _{i}^{e} $ 代表了 Encoder 第 $i$ 层的权重参数和偏置项；　　
  • $ \mathrm{W}_{i}^{d}$ 和 $\mathrm{b}_{i}^{d}$ 代表了 Dncoder 第 $i$ 层的权重参数和偏置项；　　
  • $ \hat{\mathrm{H}}_{l}$ 代表了重构后的 $\hat{\mathrm{X}}$ ；　　
  • $Z_{i} \in \mathbb{R}^{n \times d_{i}}$ 代表了 GCN 从第 $i$ 层学到的特征；　　
  • $\mathrm{Z}_{0}$ 和 $\mathrm{H}_{0} $ 代表原始数据 $\mathrm{X} $ ；　　

　　学习相应的注意力系数：

• • 将  $\mathrm{Z}_{i}$  和  $\mathrm{H}_{i}$  先进行拼接；
  • 将上述拼接的 $ \left[\mathrm{Z}_{i} \| \mathrm{H}_{i}\right] \in \mathbb{R}^{n \times 2 d_{i}}$  ，进行全连接操作；　　
  • 将上述结果使用激活函数 LeakyReLU ；　　
  • 最后再使用 softmax function 和 $\ell_{2}$  normalization；　　

　　可以公式化为 ：

　　　　$\mathrm{M}_{i}=\ell_{2}\left(\operatorname{softmax}\left(\left(\text { LeakyReLU }\left(\left[\mathrm{Z}_{i} \| \mathrm{H}_{i}\right] \mathrm{W}_{i}^{a}\right)\right)\right)\right)\quad \quad\quad(4)$

　　其中：

• • $\mathrm{M}_{i}=\left[\mathrm{m}_{i, 1} \| \mathrm{m}_{i, 2}\right] \in \mathbb{R}^{n \times 2}$ 是 attention coefficient matrix  ，且 每项大于 0；
  • $\mathrm{m}_{i, 1}$，$ \mathrm{~m}_{i, 2}$ 是衡量 $\mathrm{Z}_{i}$、$\mathrm{H}_{i}$ 重要性的权重向量；

　　融合第 $i$ 层的 GCN 的特征 $Z_{i}$ 和  AE 的特征  $ \mathrm{H}_{i} $ ：

　　　　$\mathrm{Z}_{i}^{\prime}=\left(\mathrm{m}_{i, 1} 1_{i}\right) \odot \mathrm{Z}_{i}+\left(\mathrm{m}_{i, 2} 1_{i}\right) \odot \mathrm{H}_{i}\quad \quad \quad (5)$

　　其中：

• • $1_{i} \in \mathbb{R}^{1 \times d_{i}}$ 代表着全 $1$ 向量；
  • $ '\odot'$ 代表着  Hadamard product  ；

　　将上述生成的  $Z_{i}^{\prime} \in   \mathbb{R}^{n \times d_{i}}$  当作第 $i+1$ 层 GCN 的输入，获得 $\mathrm{Z}_{i+1}$  ：

　　　　$\mathrm{Z}_{i+1}=\text { LeakyReLU }\left(\mathrm{D}^{-\frac{1}{2}}(\mathrm{~A}+\mathrm{I}) \mathrm{D}^{-\frac{1}{2}} \mathrm{Z}_{i}^{\prime} \mathrm{W}_{i}\right)\quad \quad (6$

　　其中

• • GCN 原始模型中的邻接矩阵 $A$ 变形为 $ D^{-\frac{1}{2}}(A+  I)  \mathrm{D}^{-\frac{1}{2}}$ ；
  • $\mathrm{I} \in \mathbb{R}^{n \times n}$ ；

2.2 （SWF）Scale-wise Fusion

　　将  multi-scale features $Z_{i}$  拼接在一起。

　　　　$\mathrm{Z}^{\prime}=\left[\mathrm{Z}_{1}\|\cdots\| \mathrm{Z}_{i}\|\cdots\| \mathrm{Z}_{l} \| \mathrm{Z}_{l+1}\right]$

　　其中：

• • $\mathrm{Z}_{l+1}=\mathrm{H}_{l} \in   \mathbb{R}^{n \times d_{l}}$  表示  $\mathrm{Z}_{l+1}$  的信息只来自自编码器。

　　将上述生成的 $\mathrm{Z}^{\prime}$ 放入全连接网络，并使用  $\text { softmax- } \ell_{2}$  标准化：

　　　　$\mathbf{U}=\Upsilon_{A}\left(\Xi_{j=1}^{l+1} \mathbf{Z}_{j} \mathbf{W}^{s}\right)  \quad \quad\quad(7)$

　　即：

　　　　$\mathrm{U}=\ell_{2}\left(\operatorname{softmax}\left(\operatorname{LeakyReLU}\left(\left[\mathrm{Z}_{1}\|\cdots\| \mathrm{Z}_{i}\|\cdots\| \mathrm{Z}_{l} \| \mathrm{Z}_{l+1}\right] \mathrm{W}^{s}\right)\right)\right)  $

　　其中：

• • $\mathrm{U}=\left[\mathrm{u}_{1}\|\cdots\| \mathrm{u}_{i}\|\cdots\| \mathrm{u}_{l} \| \mathrm{u}_{l+1}\right] \in \mathbb{R}^{n \times(l+1)}$  且每个数大于 $0$ ；
  • $u_{i}$  代表了  $\mathrm{Z}_{i}$  的  parallel attention coefficient ；

　　为了进一步探究多尺度特征，考虑在 attention 系数上施加一个相应的权重：

　　　　$\mathbf{Z}^{\prime}=\Xi_{j=1}^{l+1}\left(\left(\mathbf{u}_{j} \mathbf{1}_{j}\right) \odot \mathbf{Z}_{j}\right)    \quad \quad\quad(8)$

　　即：

　　　　$\mathrm{Z}^{\prime}= {\left[\left(\mathrm{u}_{1} 1_{1}\right) \odot \mathrm{Z}_{1}\|\cdots\|\left(\mathrm{u}_{i} 1_{i}\right) \odot \mathrm{Z}_{i}\|\cdots\|\left(\mathrm{u}_{l} 1_{l}\right) \odot \mathrm{Z}_{l} \|\right.} \left.\left(\mathrm{u}_{l+1} 1_{l+1}\right) \odot \mathrm{Z}_{l+1}\right]  $

　　$ Z^{\prime}$ 将作为最终预测的输入，预测输出为 $Z \in \mathbb{R}^{n \times k} $ ，其中  $k$ 代表聚类数。

　　　　$\begin{array}{l}\mathrm{Z}=\operatorname{softmax}\left(\mathrm{D}^{-\frac{1}{2}}(\mathrm{~A}+\mathrm{I}) \mathrm{D}^{-\frac{1}{2}} \mathrm{Z}^{\prime} \mathrm{W}\right) \\\text { s.t. } \quad \sum_{j=1}^{k} z_{i, j}=1, z_{i, j}>0\end{array}  \quad \quad\quad (9)$

2.3 （DWF）Distribution-wise Fusion

　　

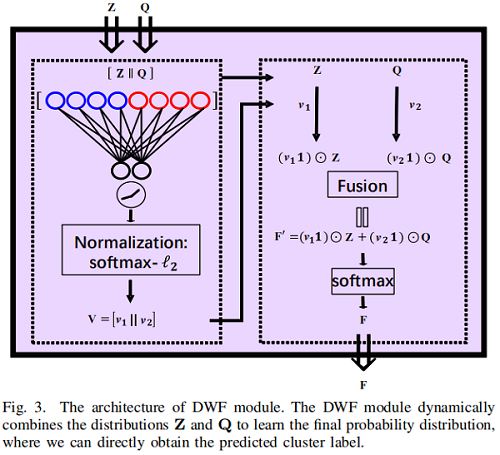
　　分布 $Z$ 和 $Q$ 分别由 $\text{Eq.9}$ 和 $\text{Eq.1}$ 得到，它们在表示数据的内在结构和聚类分配方面存在其优缺点。因此，同时考虑这两种分布能够更好地利用潜在的鉴别信息来提高性能。所以，我们提出了一种新的分布级融合(DWF)模块来自适应地利用 $Z$ 和 $Q$ 来生成最终的聚类结果。Figure 3 显示了整个体系结构。

　　　　$\mathbf{V}=\left[\mathbf{v}_{1} \| \mathbf{v}_{2}\right]=\Upsilon_{A}([\mathbf{Z} \| \mathbf{Q}] \hat{\mathbf{W}}) \quad \quad\quad (10)$

　　其中 $\mathbf{V} \in \mathbb{R}^{n \times 2}$ 为注意系数矩阵，$ \hat{\mathbf{W}}$ 是通过全连接层学习的权矩阵。

　　然后，我们自适应地利用 $Z$ 和 $Q$ ：

　　　　$\mathbf{F}=\left(\mathbf{v}_{1} \mathbf{1}\right) \odot \mathbf{Z}+\left(\mathbf{v}_{2} \mathbf{1}\right) \odot \mathbf{Q} \quad \quad\quad (11)$

　　其中，$1 \in \mathbb{R}^{1 \times k}$ 表示全 $1$ 向量。最后，我们应用 softmax 函数将 $F$ 归一化

　　　　$\mathbf{F}=\operatorname{softmax}(\mathbf{F}) \quad s.t. \quad \sum\limits _{j=1}^{k} f_{i, j}=1, \quad f_{i, j}>0  \quad \quad\quad (12)$

　　当网络经过良好的训练时，我们可以通过 $F$ 直接推断出预测的聚类标签，即：

　　　　$y_{i}=\underset{j}{\arg \max } f_{i, j} \quad \text { s.t. } \quad j=1, \cdots, k   \quad \quad\quad (13)$

　　其中，$y_{i} $ 是 $\mathbf{x}_{i}$ 的预测标签。这样，集群结构就可以显式地用 $F$ 来表示。

2.4 Dual Self-supervision

2.4.1 Soft Self-supervision

　　由于我们利用高置信度分配，利用软赋值(即概率分布 $Q$ 和 $Z$ )迭代地细化聚类，因此我们将这种监督策略称为软自监督(SSS)策略。具体地说，由于 $Z$ 通过 $HWF$ 和 $SWF$ 模块涉及丰富的信息。

　　我们首先通过平方 $z_{i, j}$，推导出一个辅助分布 $P$，即:

　　　　${\large p_{i, j}=\frac{z_{i, j}^{2} / \sum\limits _{i^{\prime}=1}^{n} z_{i^{\prime}, j}}{\sum\limits _{j^{\prime}=1}^{k} z_{i, j}^{2} / \sum\limits _{i^{\prime}=1}^{n} \sum\limits _{j^{\prime}=1}^{k} z_{i^{\prime}, j^{\prime}}}}   \quad \quad\quad (14)$

　　然后，我们使用一个高度一致的分布对齐来训练我们的模型：

　　　　$\begin{aligned}\mathcal{L}_{S} &=\lambda_{1} *(K L(\mathbf{P}, \mathbf{Z})+K L(\mathbf{P}, \mathbf{Q}))+\lambda_{2} * K L(\mathbf{Z}, \mathbf{Q}) \\&=\lambda_{1} \sum\limits _{i}^{n} \sum\limits _{j}^{k} p_{i, j} \log \frac{p_{i, j}^{2}}{z_{i, j} q_{i, j}}+\lambda_{2} \sum\limits _{i}^{n} \sum\limits _{j}^{k} z_{i, j} \log \frac{z_{i, j}}{q_{i, j}},\end{aligned} \quad \quad\quad (15)$

2.4.2 Hard Self-supervision

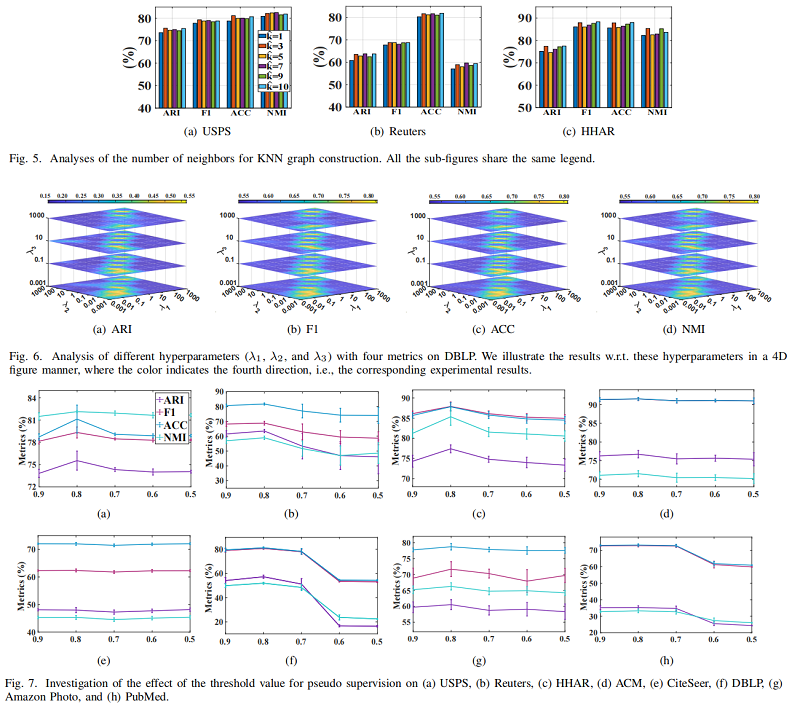
　　为了进一步利用聚类分配中可用的鉴别信息，我们引入了伪监督技术[45]，并将伪标签 $\hat{y}_{i}$ 设置为 $\hat{y}_{i}=y_{i}$。考虑到伪标签可能包含许多不正确的标签，我们通过一个较大的阈值 $r$ 来选择高可信度的标签作为监督信息，即：

　　　　$g_{i, j}=\left\{\begin{array}{ll}1 & \text { if } f_{i, j} \geq r \\0 & \text { otherwise }\end{array}\right.  \quad \quad\quad (16)$

　　在实验中，我们设置 $r=0.8$。然后，我们利用高置信度的伪标签来监督网络训练，即:

　　　　$\mathcal{L}_{H}=\lambda_{3} \sum\limits _{i} \sum\limits _{j} g_{i, j} * \Upsilon_{C E}\left(f_{i, j}, \Upsilon_{O H}\left(\hat{y}_{i}\right)\right)   \quad \quad\quad (17)$

　　其中，$\lambda_{3}>0$ 为权衡参数，$\Upsilon_{C E}$ 为交叉熵损失，$\Upsilon_{O H}$ 将 $ \hat{y}_{i}$ 转换为 one-hot 形式。如 Figure 4 所示，伪标签将集群分配转移到硬单热编码中，因此我们将其命名为硬自我监督(HSS)策略。

　　组合 $\text{Eq.3}$，$\text{Eq.15}$ 和 $\text{Eq.17}$，我们的整体损失函数可以写成

　　　　$\mathcal{L}=\min _{\mathbf{F}}\left(\mathcal{L}_{R}+\mathcal{L}_{S}+\mathcal{L}_{H}\right)   \quad \quad\quad (18)$

　　整个训练过程如 Algorithm 1 所示：

　　 

3 Experiments

数据集

　　

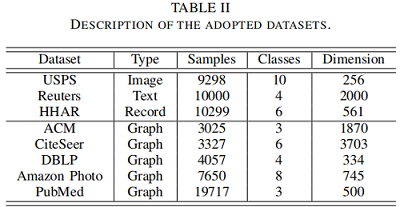
实验补充

　　对于非图数据集(即 USPS、Reuters 和 HHAR)缺乏拓扑图，使用了一种典型的图构造方法来生成它们的图数据。具体来说，我们首先利用余弦距离来计算相似度矩阵 $S$，即：

　　　　$\mathbf{S}=\frac{\mathbf{X} \mathbf{X}^{\top}}{\|\mathbf{X}\|_{F}\left\|\mathbf{X}^{\top}\right\|_{F}}    \quad \quad\quad (19)$

　　式中，$\|\mathbf{X}\|_{F}=\sqrt{\sum_{i=1}^{n} \sum_{j=1}^{d}\left|x_{i, j}\right|^{2}}$ 和 $ \mathbf{X}^{\top}$ 分别表示 $F$ 范数和 $\mathbf{X}$ 的转置运算。然后，我们保留每个样本的 $top- \hat{k}$ 近邻，以构造一个无向的 $\hat{k}$-近邻(KNN)图。所构造的 KNN 图可以描述数据集的拓扑结构，因此被用作GCN输入。

聚类结果

　　

消融实验

　　

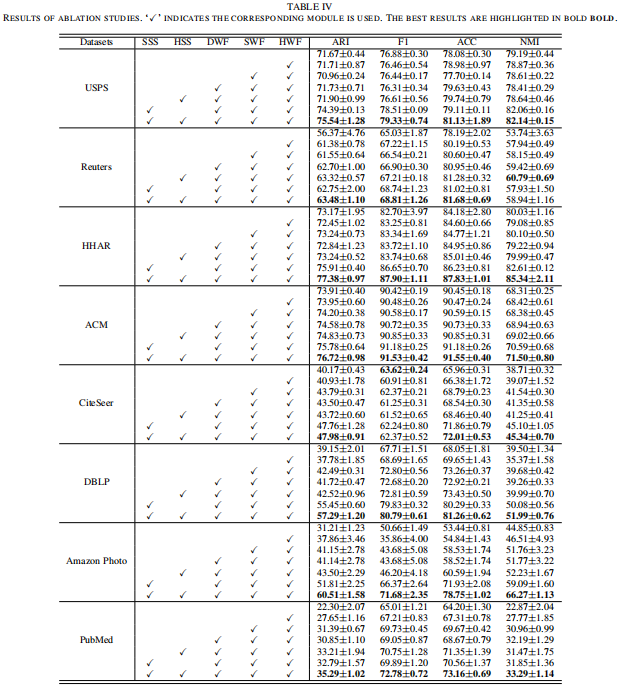
参数分析

　　

4 Conclusion

　　我们提出了一种新的深度嵌入聚类方法，同时增强了嵌入学习和聚类分配。具体来说，我们首先设计了异质性和尺度上的融合模块来自适应地学习判别表示。然后，我们利用分布融合模块，通过基于注意力的机制实现聚类增强。最后，我们提出了一种具有库回-莱布勒散度损失的软自我监督策略和一种具有伪监督损失的硬自我监督策略来利用聚类分配中现有的鉴别信息。定量和定性的实验和分析表明，我们的方法始终优于最先进的方法。我们还提供了全面的消融研究来验证我们的网络的有效性和优势。今后，我们将研究先进的图构造方法。