生产计划问题(动态规划)—R实现
动态规划
动态规划(英语:Dynamic programming,简称 DP),是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。网上有很多动态规划的代码实现文章,但是如何理解动态规划的思想才是最关键的,尤其如何理解成这是一个多阶段的决策过程尤为重要。
一、动态规划理论基础
1.动态规划经典实例
动态规划是多阶段决策(序贯决策)数学模型,下例是一个经典的面试题。
【例题】在一个夜黑风高的晚上,有n(n <= 50)个小朋友在桥的这边,现在他们需要过桥,但是由于桥很窄,每次只允许不大于两人通过,他们只有一个手电筒,所以每次过桥的两个人需要把手电筒带回来,i号小朋友过桥的时间为T[i],两个人过桥的总时间为二者中时间长者。问所有小朋友过桥的总时间最短是多少。

每次过桥的时候最多两个人,如果桥这边还有人,那么还得回来一个人(送手电筒),也就是说N个人过桥的次数为2N-3(倒推,当桥这边只剩两个人时只需要一次,三个人的情况为来回一次后加上两个人的情况…)。有一个人需要来回跑,将手电筒送回来(也许不是同一个人,realy?!)这个回来的时间是没办法省去的,并且回来的次数也是确定的,为N-2,如果是我,我会选择让跑的最快的人来干这件事情,但是我错了…如果总是跑得最快的人跑回来的话,那么他在每次别人过桥的时候一定得跟过去,于是就变成就是很简单的问题了,花费的总时间:
T = minPTime * (N-2) + (totalSum-minPTime)
来看一组数据 四个人过桥花费的时间分别为 1 2 5 10,按照上面的公式答案是19,但是实际答案应该是17。
具体步骤是这样的:
第一步:1和2过去,花费时间2,然后1回来(花费时间1);
第二歩:3和4过去,花费时间10,然后2回来(花费时间2);
第三步:1和2过去,花费时间2,总耗时17。
所以之前的贪心想法是不对的。我们先将所有人按花费时间递增进行排序,假设前i个人过河花费的最少时间为opt[i],那么考虑前i-1个人过河的情况,即河这边还有1个人,河那边有i-1个人,并且这时候手电筒肯定在对岸,所以opt[i] = opt[i-1] + a[1] + a[i] (让花费时间最少的人把手电筒送过来,然后和第i个人一起过河)如果河这边还有两个人,一个是第i号,另外一个无所谓,河那边有i-2个人,并且手电筒肯定在对岸,所以opt[i] = opt[i-2] + a[1] + a[i] + 2a[2] (让花费时间最少的人把电筒送过来,然后第i个人和另外一个人一起过河,由于花费时间最少的人在这边,所以下一次送手电筒过来的一定是花费次少的,送过来后花费最少的和花费次少的一起过河,解决问题),所以 opt[i] = min{opt[i-1] + a[1] + a[i] , opt[i-2] + a[1] + a[i] + 2*a[2] }。
2.动态规划的基本原理
动态规划与分治法类似,都是把大问题拆分成小问题,通过寻找大问题与小问题的递推关系,解决一个个小问题,最终达到解决原问题的效果。但不同的是,分治法在子问题和子子问题等上被重复计算了很多次,而动态规划则具有记忆性,通过填写结果二维表把所有已经解决的子问题答案纪录下来,这样在解决下一个新问题时需要用到前面子问题的结果,这样,每一步计算的结构都是在上一步的结果基础之上完成,这样就可以保证所有的子问题结果都满足最优性原理。用动态规划解决问题的核心就在于填写结果二维表,二维表填写完毕,最优解也就找到了。
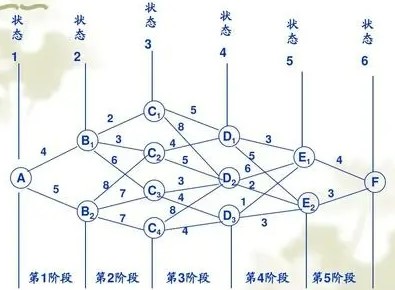
最优性原理是动态规划的基础,"多阶段决策过程的最优决策序列具有这样的性质:不论初始状态和初始决策如何,对于前面决策所造成的某一状态而言,其后各阶段的决策序列必须构成最优策略"。也就是说,每一次子问题的尝试解决都是在之前的已经解决的子问题的基础之上进行;这样就保证了每一次子问题解决都是最优结果。【每一步子问题的解决都保证了最优】
二、生产计划问题
工厂生产某种产品,每单位(千件)的成本为 1(千元),每次开工的固定成本为 3 (千元),工厂每季度的最大生产能力为 6(千件)。经调查,市场对该产品的需求量第一、二、三、四季度分别为 2,3,2,4(千件)。如果工厂在第一、二季度将全年的需求都生产出来,自然可以降低成本(少付固定成本费),但是对于第三、四季度才能上市的产品需付存储费,每季每千件的存储费为 0.5(千元)。还规定年初和年末这种产品均无库存。试制定一个生产计划,即安排每个季度的产量,使一年的总费用(生产成本和存储费)最少。
1. 动态规划基本方程(建模)
这一类生产计划问题(Production planning problem),阶段按计划时间自然划分为4个阶段,状态变量定义为每阶段开始时的储存量x(k),决策变量为每个阶段的产量u(k),记每个阶段的需求量(已知量)为d(k),则状态转移方程为:
x(k+1) = x(k) + u(k) − d(k) ( x(k)≥0, k=1,2,...,n )
(1)设每阶段开工的固定成本费为a,生产单位数量产品的成本费为b,每阶段单位数量产品的储存费为c,阶段指标为阶段的生产成本和储存费之和,即
if u(k)>0
v(x(k), u(k)) = cx(k) + (a + bu(k))
if u(k)=0
v(x(k), u(k)) = cx(k) + 0
(2)最优值函数f(x(k))为从第k段的状态x(k)出发到过程终结的最小费用,满足:
f(x(k)) = min(v(x(k), u(k)) + f(x(k+1)))
2. R求解程序
# 每阶段单位数量产品的储存费为c
C=0.5
# 每阶段开工的固定成本费为a
A = 3;
# 生产单位数量产品的成本费为b
B = 1;
# 市场对该产品的需求量数组
ds <- c(2, 3, 2, 4);
# 市场对该产品的需求量函数
d <- function(k) {
return (ds[k])};
# 生产目标,所有初始化为NA,在每次遍历的时候,需要更新这个值
us <- rep(NA, times=length(ds));
u <- function(k) {
return (us[k]);
}
# 每阶段开始时的储存量x(x)
x <- function(k) {
if(k <= 1) {
result <- 0;
} else {
result <- x(k-1) + u(k-1) - d(k-1);
}
return (result);
}
# 阶段的生产成本和储存费之和
vs <- c();
v <- function(k) {
if(u(k) == 0) {
vs[k] <- C*x(k);
}
if(u(k)>0) {
vs[k] <- C*x(k) + (A + B*u(k));
}
return (vs[k]);
}
f <- function(k) {
# 设置终止条件,如果为第k+1季度,则返回
#f(x(k))=min(v(x(k), u(k)) + f(x(k+1)))
if(k == (length(ds)+1)) {
result <- 0;
} else {
result <- v(k) + f(k+1);
}
return (result);
}
uss <- expand.grid(s1=c(0:sum(ds)), s2=c(0:sum(ds)), s3=c(0:sum(ds)), s4=c(0:sum(ds)));
uss <- data.matrix(uss[which(rowSums(uss)==sum(ds)),]);
#i<- 2
#uss[which(rowSums(matrix(uss[,1:i], ncol=i))>=sum(ds[1:i])),];
for(i in 1:length(ds)) {
uss <- uss[which(rowSums(matrix(uss[,1:i], ncol=i)) >= sum(ds[1:i])),];
}
rs = c();
for(i in 1:nrow(uss)) {
# 重新设置us值
us <- uss[i,];
rs[i] <- f(1);
}
min(rs)
uss[which(rs == min(rs)),]
3. 结果计算
min(rs)
[1] 20.5
uss[which(rs == min(rs)), ]
s1 s2 s3 s4
870 5 0 6 0
6920 7 0 0 4
三、动态规划总结
动态规划是一种解决最优化、搜索和计数问题的通用技术,这些问题都可以被分解为多个子问题。可以从背包问题的两个思路来了解动态规划,一个是利用物品个数和背包容量来说明阶段间关系,即“前i-1件物品放入剩下的容量为v-c[i]的背包中”;另一个就是直接从背包容量角度去考虑价值,新增的容量所带来的不同价值,记录各个物品新增所造成的价值变化,虽然抽象,但空间复杂度少很多。很多组合优化问题都可以归结背包问题,因为很多问题本质是因设备能力有限所造成的的瓶颈带来求解困难。
原创文献
(数学建模动态规划的小案例之R代码实现——生产计划问题)[https://blog.csdn.net/qq_44217143/article/details/99115342]
生产计划问题(动态规划)—R实现的更多相关文章
- SAP 工厂日生产计划待排维护
*&---------------------------------------------------------------------* *& Report ZPPR0024 ...
- MRP生产计划模式在多品种小批量生产过程中遭遇挑战
传统的MPS主生产计划和MRP物料需求计划的方式,已很难适应按需生产环境,很多企业正在转向按需生产环境,按需生产的最大的挑战是模拟计算CTP可以承诺交期.准时交货和应对不确定的插单等变化.不仅需要订单 ...
- 关于APS在企业生产计划上的应用
本人本身是一个码农,已经服务了共和国各项事业(好像是说得有点漂,没办法段子看多了)大约一半工作时候了(按60岁退休的话),从一线的小码农,到现在成了老农,出产了不少或优或劣的各种码,几乎啥都做过.近几 ...
- 易普优APS应用案例:线束行业生产计划排产
一.线束行业生产现状 (1)产品种类以及标准繁多,生产计划难协调 线束行业的生产,虽然原材料不多,但线束产品却多达几万种.一般线束企业,虽然不是每个月都生产数万种产品,但每月生产的产品品种在300种以 ...
- 什么是APS高级计划排程(生产计划排产)系统主要功能模块有哪些?
什么是APS高级计划排程(生产计划排产)系统? APS高级计划排程(高级计划排产)系统主要解决“在有限产能条件下,交期产能精确预测.工序生产与物料供应最优详细计划”的问题.APS高级计划排程(高级计划 ...
- APS中生产计划排程模块的基本原理
高级计划系统(APS)作为ERP和MES的补充,用于协调物流.开发瓶颈资源和保证交货日期. APS包括需求和供应计划.运输和生产计划排程等各种供应链计划模块,本文主要介绍APS中生产计划排程模块的基本 ...
- 为什么众多软件厂商无法提供APS高级计划排程系统?工厂目前生产计划是怎么排产的?
一.行业现状如想了解一下目前现状,去考察一下上了ERP的企业,会发现一个有趣的现象该企业无论ERP软件搞得如何如火如荼,似乎都与生产调度人员无关. 车间里或者生产线上的生产作业计划.生产过程的调度和管 ...
- BZOJ_1613_ [Usaco2007_Jan]_Running_贝茜的晨练计划_(动态规划)
描述 http://www.lydsy.com/JudgeOnline/problem.php?id=1613 n分钟,疲劳值上限是m,开始时疲劳值为0.第i分钟可以跑d[i]米.在某一时刻,如果疲劳 ...
- r.js合并实践 --项目中用到require.js做生产时模块开发 r.js build.js配置详解
本文所用源代码已上传,需要的朋友自行下载:点我下载 第一步: 全局安装 npm install -g requirejs 第二步: 1.以下例子主要实现功能, 1)引用jq库获取dom中元素文本, ...
- Lingo求解线性规划案例1——生产计划问题
凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 说明: Lingo版本: 某工厂明年根据合同,每个季度末 ...
随机推荐
- Kubernetes快速部署
Kubernetes快速部署 kubernetes简介 kubernetes,是一个全新的基于容器技术的分布式架构领先方案,是谷歌严格保密十几年的秘密武器----Borg系统的一个开源版本,于2014 ...
- WebApi 下载三维zip文件并预览
// 异步加载 const LoadObj = async (key?: string) => { LoadState.value = true var objStr, mtlStr var i ...
- Spring Boot中使用过滤器和拦截器
过滤器(Filter)和拦截器(Interceptor)是Web项目中常用的两个功能,本文将简单介绍在Spring Boot中使用过滤器和拦截器来计算Controller中方法的执行时长,并且简单对比 ...
- js中函数(方法)注释
原文链接:https://blog.csdn.net/tianxintiandisheng/article/details/103764074 实例 /** * @function 处理表格的行 * ...
- MongoDB:内嵌文档查询匹配 查询集合中的文档
1.db.getCollection('Notification').find({ Title:{$regex:/班/}, "Message.TargetUrl":{$regex: ...
- constexpr 和常量表达式
常量表达式(是const expression) 是指值不会改变并且在编译过程中就能得到计算结果的表达式.显然,字面值属于常量表达式,用常量 表达式初始化的const 对象也是常量表达式.后面将会提到 ...
- VBA类模块完全教程(www.accessoft.com软件网)
这份礼物送给现在想学习类知识或曾经学过但因为各种原因没有"修成正果"的朋友,我期望的结果是这篇文章后,您可以在类模块中像在标准模块中写代码一样熟练,我也期望不至于太乏味而使您没有耐 ...
- web自动化--窗口切换
窗口切换 handles = driver.window_handles ------获取所有窗口句柄,返回的数据是一个列表类型 driver.switch_to.window(handles[-1] ...
- C/C++ 数据结构使用数组实现队列的基本操作
//使用数组实现队列 #include <iostream> #include <Windows.h> using namespace std; #define MAXSIZE ...
- Codeforces Round #809 (Div. 2) A-E
Codeforces Round #809 (Div. 2) 2022/7/19 下午VP 传送门:https://codeforces.com/contest/1706 A. Another Str ...
