2020 Multi-University Training Contest 1 . Fibonacci Sum 水题改编

题意很简单，就是让你求这个东西，这个时候你发现，原题？？？？

https://blog.csdn.net/acdreamers/article/details/23039571

哦，只是原来写过的哪一题的C是1，这个是1e18. 想都不用想，直接二项式展开，求等比数列的前n项和。

你会得到第i项（一共k项）:。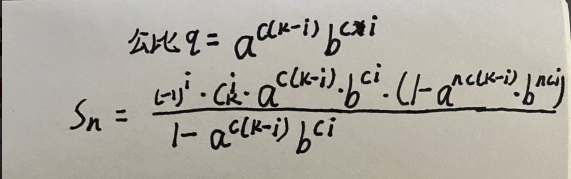

这个时候理所当然的想先用二次剩余求出来那几个用到的东西，a，b，1/sqrt(5)。

1你用快速幂求了一下，一交，tle了。

2 然后发现每个都求快速幂太蠢了，所以又优化优化，优化到除了求分母的逆元需要用到快速幂其他的都可以由上一项推出来，然后再交，又wa了。

3 哦，原来这是等比数列，分母是1-q，如果q是1那不就错了吗？所以特判一下如果q是1，加的就是n*a1，a1是几？你看这个Sn，忽略这个组合数，a1不就和q完全相等吗，是1！ 就这样a了。

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define met(a, b) memset(a, b, sizeof(a))
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define bep(i, a, b) for(int i = a; i >= b; i--)
#define pb push_back
#define mp make_pair
#define debug cout << "KKK" << endl
#define ls num*2
#define rs num*2+1
#define re return
using namespace std;
const ll mod = 1e9 + 9;
const double PI = acos(-1);
const ll INF = 2e18+1;
const int inf = 1e9+5;
const double eps = 1e-7;
const int maxn = 1e5 + 5;
// 逆元
// sqrt(5) = 383008016;
// a = (1+sqrt(5))/2 = 691504013;
// b = (1-sqrt(5))/2 = 308495997;
// 1/sqrt(5) = 276601605;
ll A = 691504013, B = 308495997;
ll sqrt5 = 383008016, invsqrt5 = 276601605;
ll qsm(ll a, ll n){
    ll res = a%mod, sum = 1;
    while(n){
        if(n&1) sum = (sum*res)%mod;
        res = (res*res)%mod;
        n >>= 1;
    }
    return sum;
}

ll fac[maxn], f[maxn], inv[maxn];
ll C(ll m, ll n){
    if(m < n) return 0;
    if(n == 0 || m == n) return 1;
    return fac[m]*inv[n]%mod*inv[m-n]%mod;
}
void init(){
    fac[1] = 1;
    f[1] = 1;
    inv[1] = 1;
    for(ll i = 2; i <= 100000; i++){
        fac[i] = fac[i-1]*i%mod;
        f[i] = (mod - mod/i)*f[mod%i]%mod;
        inv[i] = inv[i-1]*f[i]%mod;
    }
}

ll sac[maxn], sbc[maxn];
int main(){
    // ios::sync_with_stdio(false);
    // cin.tie(0); cout.tie(0);
    init();
    int t; scanf("%d", &t);
    while(t--){
        ll n, c, k;
        scanf("%lld%lld%lld", &n,&c,&k);
        // n = 1e18, c = 1e18, k = 1e5;
        ll res = qsm(invsqrt5, k);
        ll ans = 0, flag = -1;
        ll x, y;
        ll ac = qsm(A, c), bc = qsm(B, c);
        sac[0] = 1, sbc[0] = 1;
        sac[1] = ac, sbc[1] = bc;
        rep(i, 1, k){
            sac[i] = sac[i-1]*ac%mod;
            sbc[i] = sbc[i-1]*bc%mod;
        }
        ll acn = qsm(qsm(A, c), n);
        ll bcn = qsm(qsm(B, c), n);
        ll invacn = qsm(acn, mod-2);
        ll invbcn = qsm(bcn, mod-2);
        ll now_acn = qsm(acn, k), now_bcn = 1;
        for(ll i = 0; i <= k; i++){
            flag *= -1;
            ll q = sac[k-i] * sbc[i] % mod;
            if(q == 1){
                q = (n%mod)*C(k, i) % mod;
                ans = (ans + flag*q%mod + mod) % mod;
            }
            else{
                x = (C(k, i)*sac[k-i]%mod) * sbc[i] % mod;
                x = (1-(now_acn * now_bcn % mod) + mod) % mod * x % mod;
                y = (1 - (sac[k-i] * sbc[i])%mod ) % mod;
                y = qsm(y, mod-2);
                ans = (ans + flag*x*y%mod + mod)%mod;
            }
            now_acn = (now_acn * invacn) % mod;
            now_bcn = (now_bcn * bcn) % mod;
        }
        cout << ans*res%mod << endl;
    }
    return 0;
}