bzoj2564集合的面积

题目描述

　　对于一个平面上点的集合P={(xi,yi )}，定义集合P的面积F(P)为点集P的凸包的面积。
　　对于两个点集A和B，定义集合的和为：
　　A+B={(xiA+xjB,yiA+yjB ):(xiA,yiA )∈A,(xjB,yjB )∈B}
　　现在给定一个N个点的集合A和一个M个点的集合B，求2F(A+B)。

---

输入格式

　第一行包含用空格隔开的两个整数，分别为N和M；
　　第二行包含N个不同的数对，表示A集合中的N个点的坐标；
　　第三行包含M个不同的数对，表示B集合中的M个点的坐标。

　

---

输出格式

　一共输出一行一个整数，2F(A+B)。

---

数据规模和约定
　　对于30%的数据满足N ≤ 200，M ≤ 200；
　　对于100%的数据满足N ≤ 10^5，M ≤ 10^5，|xi|, |yi| ≤ 10^8。

---

• 题解：

  • 如果一个点成为了和$A+B$的凸包，那么一定同时在$A$和$B$的凸包上;
  • 设$A+B$看成把凸包$A$平移后放在凸包$B$上，发现在两个凸包上组合成新的凸包的点对是单调的；
  • 类似$graham$维护两个指针；
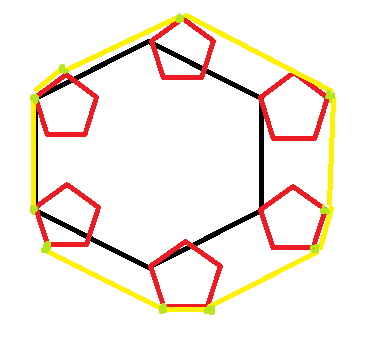
  • 不太好说，附图，但是建议自己$YY$：
    

  •  #include<bits/stdc++.h>
     #define ll long long
     using namespace std;
     const int N=;
     int n,m,cnt1,cnt2,Cnt;
     char gc(){
         static char*p1,*p2,s[];
         if(p1==p2)p2=(p1=s)+fread(s,,,stdin);
         return (p1==p2)?EOF:*p1++;
     }
     int rd(){
         int x=,f=; char c=gc();
         while(c<''||c>''){if(c=='-')f=-;c=gc();}
         while(c>=''&&c<=''){x=(x<<)+(x<<)+c-'';c=gc();}
         return x*f;
     }
     struct poi{
         int x,y;
         poi(int _x=,int _y=):x(_x),y(_y){};
         poi operator +(const poi&A)const{return poi(x+A.x,y+A.y);}
         poi operator -(const poi&A)const{return poi(x-A.x,y-A.y);}
         bool operator <(const poi&A)const{return x==A.x?y<A.y:x<A.x;}
     }p1[N],p2[N],q1[N],q2[N],Q[N];
     ll crs(poi A,poi B){return (ll)A.x*B.y-(ll)A.y*B.x;}
     void convex(poi *p,poi *q,int&tot,int&cnt){
         if(tot==){q[cnt=]=q[]=p[];return;}
         sort(p+,p+tot+);
         q[cnt=]=p[];
         for(int i=;i<=tot;i++){
             while(cnt> && crs(q[cnt]-q[cnt-],p[i]-q[cnt])<=)cnt--;
             q[++cnt]=p[i];
         }
         int now=cnt;
         for(int i=tot-;i;i--){
             while(cnt>now && crs(q[cnt]-q[cnt-],p[i]-q[cnt])<=)cnt--;
             q[++cnt]=p[i];
         }
         cnt--;
     }
     int main(){
         #ifndef ONLINE_JUDGE
         freopen("bzoj2564.in","r",stdin);
         freopen("bzoj2564.out","w",stdout);
         #endif
         n=rd();m=rd();
         for(int i=;i<=n;i++)p1[i].x=rd(),p1[i].y=rd();
         for(int i=;i<=m;i++)p2[i].x=rd(),p2[i].y=rd();
         convex(p1,q1,n,cnt1);
         convex(p2,q2,m,cnt2);
         int i,j;
         for(i=,j=;i<=cnt1;i++){
             Q[++Cnt]=q1[i]+q2[j];
             while(j<=cnt2&&crs(q2[j+]-q2[j],q1[i+]-q1[i])>){
                 Q[++Cnt]=q1[i]+q2[++j];
             }
         }
         for(;j<=cnt2+;j++)Q[++Cnt]=q1[i]+q2[j];
         Cnt--;
         ll ans=;
         for(i=;i<Cnt;i++)ans += crs(Q[i]-Q[],Q[i+]-Q[]);
         printf("%lld\n",ans);
         return ;
     }

    bzoj2564