Codeforces 804D Expected diameter of a tree

D. Expected diameter of a tree

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Pasha is a good student and one of MoJaK's best friends. He always have a problem to think about. Today they had a talk about the following problem.

We have a forest (acyclic undirected graph) with n vertices and m edges. There are q queries we should answer. In each query two vertices v and u are given. Let V be the set of vertices in the connected component of the graph that contains v, and U be the set of vertices in the connected component of the graph that contains u. Let's add an edge between some vertex 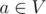 and some vertex in  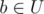and compute the value d of the resulting component. If the resulting component is a tree, the value d is the diameter of the component, and it is equal to -1 otherwise. What is the expected value of d, if we choose vertices a and b from the sets uniformly at random?

Can you help Pasha to solve this problem?

The diameter of the component is the maximum distance among some pair of vertices in the component. The distance between two vertices is the minimum number of edges on some path between the two vertices.

Note that queries don't add edges to the initial forest.

Input

The first line contains three integers n, m and q(1 ≤ n, m, q ≤ 105) — the number of vertices, the number of edges in the graph and the number of queries.

Each of the next m lines contains two integers ui and vi (1 ≤ ui, vi ≤ n), that means there is an edge between vertices ui and vi.

It is guaranteed that the given graph is a forest.

Each of the next q lines contains two integers ui and vi (1 ≤ ui, vi ≤ n) — the vertices given in the i-th query.

Output

For each query print the expected value of d as described in the problem statement.

Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6. Let's assume that your answer is a, and the jury's answer is b. The checker program will consider your answer correct, if .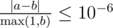

Examples

input

3 1 2
1 3
3 1
2 3

output

-1
2.0000000000

input

5 2 3
2 4
4 3
4 2
4 1
2 5

output

-1
2.6666666667
2.6666666667

Note

In the first example the vertices 1 and 3 are in the same component, so the answer for the first query is -1. For the second query there are two options to add the edge: one option is to add the edge 1 - 2, the other one is 2 - 3. In both ways the resulting diameter is 2, so the answer is 2.

In the second example the answer for the first query is obviously -1. The answer for the second query is the average of three cases: for added edges 1 - 2 or 1 - 3 the diameter is 3, and for added edge 1 - 4 the diameter is 2. Thus, the answer is .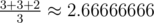

题意：

给出一个森林，q次询问，每次问把x,y两点所属的树之间任意连接一条边形成新的树的直径的期望，如果x和y在同一棵树中输出-1；

代码：

//这题算出复杂度也就解出来了。先枚举一棵树中的节点然后二分找另一棵树中的节点满足两个节点之间的距离不小于max(树1直径，
//树2直径)，他们的贡献就是各自在自己树中最远能到达的端点的距离相加再+1,否则贡献就是max(树1直径，树2直径)，这样看似是
//q*n*long(n),但是注意到所有的树的大小总和是n所以最坏是sqrt(n)棵树每棵树大小是sqrt(n),所以是q*sqrt(n)*long(n);
#include<iostream>
#include<cstdio>
#include<cstring>
#include<map>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long ll;
const int MAXN=;
int fa[MAXN],head[MAXN],tot,n,cnt,m,q,d[MAXN],f[MAXN],deep,o,oo,root[MAXN];
int a[MAXN],aa;
double size[MAXN];
map<pair<int,int>,double>mp;
vector<ll>v[MAXN],vv[MAXN];
struct Edge { int u,v,next; }edge[MAXN*];
void init()
{
    tot=cnt=;
    memset(head,-,sizeof(head));
    memset(fa,-,sizeof(fa));
    memset(f,,sizeof(f));
    memset(d,-,sizeof(d));
}
void add(int x,int y)
{
    edge[tot].u=x;edge[tot].v=y;
    edge[tot].next=head[x];
    head[x]=tot++;
    edge[tot].u=y;edge[tot].v=x;
    edge[tot].next=head[y];
    head[y]=tot++;
}
void dfs1(int x,int father,int p)
{
    v[p].push_back(x);
    for(int i=head[x];i!=-;i=edge[i].next){
        int y=edge[i].v;
        if(y==father) continue;
        fa[y]=p;
        dfs1(y,x,p);
    }
}
void dfs2(int x,int father,int sum,bool w)
{
    if(w!=) f[x]=max(f[x],sum);
    if(sum>=deep){
        deep=sum;
        if(w==) o=x;
        else if(w==) oo=x;
    }
    for(int i=head[x];i!=-;i=edge[i].next){
        int y=edge[i].v;
        if(y==father) continue;
        dfs2(y,x,sum+,w);
    }
}
int main()
{
    //freopen("in.txt","r",stdin);
    init();
    scanf("%d%d%d",&n,&m,&q);
    for(int i=;i<m;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
    }
    for(int i=;i<=n;i++){
        if(fa[i]!=-) continue;
        fa[i]=++cnt;
        v[cnt].clear();vv[cnt].clear();
        dfs1(i,,cnt);
        root[cnt]=i;
    }
    for(int i=;i<=cnt;i++){
        deep=;
        dfs2(root[i],,,);
        deep=;
        dfs2(o,,,);
        d[i]=deep;
        dfs2(oo,,,);
        aa=v[i].size();
        for(int j=;j<aa;j++) a[j]=f[v[i][j]];
        v[i].clear();
        for(int j=;j<aa;j++) v[i].push_back(a[j]);
        sort(v[i].begin(),v[i].end());
        a[aa]=;
        for(int j=aa-;j>=;j--) a[j]=a[j+]+v[i][j]+;
        for(int j=;j<=aa;j++) vv[i].push_back(a[j]);
    }
    while(q--){
        int x,y;
        scanf("%d%d",&x,&y);
        if(fa[x]==fa[y]) printf("-1\n");
        else{
            pair<int,int>p1(fa[x],fa[y]);
            if(mp[p1]>) printf("%.6f\n",mp[p1]);
            else{
                double ans=;
                int xx=fa[x],yy=fa[y];
                if(v[xx].size()<=v[yy].size()){
                    for(int i=;i<v[xx].size();i++){
                        ll tmp=lower_bound(v[yy].begin(),v[yy].end(),max(d[xx],d[yy])-v[xx][i]-)-v[yy].begin();
                        ans+=(vv[yy][tmp]+v[xx][i]*(v[yy].size()-tmp))+tmp*max(d[xx],d[yy]);
                    }
                }else{
                    for(int i=;i<v[yy].size();i++){
                        ll tmp=lower_bound(v[xx].begin(),v[xx].end(),max(d[xx],d[yy])-v[yy][i]-)-v[xx].begin();
                        ans+=(vv[xx][tmp]+v[yy][i]*(v[xx].size()-tmp))+tmp*max(d[xx],d[yy]);
                    }
                }
                double tmp1=v[xx].size(),tmp2=v[yy].size();
                ans/=(tmp1*tmp2);
                printf("%.6f\n",ans);
                mp[p1]=ans;
            }
        }
    }
    return ;
}