洛谷 P4363 [九省联考2018]一双木棋chess 解题报告

P4363 [九省联考2018]一双木棋chess

题目描述

菲菲和牛牛在一块\(n\)行\(m\)列的棋盘上下棋，菲菲执黑棋先手，牛牛执白棋后手。 棋局开始时，棋盘上没有任何棋子，两人轮流在格子上落子，直到填满棋盘时结束。

落子的规则是：一个格子可以落子当且仅当这个格子内没有棋子且这个格子的左侧及上方的所有格子内都有棋子。

棋盘的每个格子上，都写有两个非负整数，从上到下第\(i\)行中从左到右第\(j\)列的格子上的两个整数记作\(A_{i,j},B_{i,j}\) 。在游戏结束后，菲菲和牛牛会分别计算自己的得分：菲菲的得分是所有有黑棋的格子上的\(A_{i,j}\)之和，牛牛的得分是所有有白棋的格子上的\(B_{i,j}\)的和。

菲菲和牛牛都希望，自己的得分减去对方的得分得到的结果最大。现在他们想知道，在给定的棋盘上，如果双方都采用最优策略且知道对方会采用最优策略，那么，最终的结果如何。

输入输出格式

输入格式：

输入第一行包含两个正整数\(n,m\)，保证\(n,m<=10\)。

接下来\(n\)行，每行\(m\)个非负整数，按从上到下从左到右的顺序描述每个格子上的 第一个非负整数：其中第\(i\)行中第\(j\)个数表示\(A_{i,j}\) 。

接下来\(n\)行，每行\(m\)个非负整数，按从上到下从左到右的顺序描述每个格子上的 第二个非负整数：其中第\(i\)行中第\(j\)个数表示\(B_{i,j}\) 。

输出格式：

输出一个整数，表示菲菲的得分减去牛牛的得分的结果。

说明：

---

也算是第一次做这样的博弈吧，省选划水的时候没做过状压也没做过博弈。好不容易YY出了\(n+m\)轮廓线处理的方法却不清楚怎么确定最优策略。结果15分的分类讨论分居然因为读入把A,B一起读了而爆0。。

先看看最优策略如何确定的：如果双方都采用最优策略且知道对方会采用最优策略。

由此我们得，我们要使用最优策略，首先要知道对方的最优策略，然后才能确定自己的最优策略。

但是如果我们只考虑前面的已经做的状态，是无法得知最优策略的。

这时候我们反其道而行之，把当前一步可以到达的局面看成一个子问题。这个子问题已经产生了答案，它是一个规模缩小版的但已经处理完了每一步的一个游戏。我们这一步可以进入这个子问题，但进入的入口并不唯一，我们对这个不唯一进行决策，找到对自己而言的局面最大化进入。而这个子问题的最小规模又是唯一确定的，也就是最后一步。所以我们的思路是，先通过记忆化搜索进入最后一步，然后像做树形DP那样在对搜索树进行回溯的时候更新答案。

对于两个人的具体策略而言，我们不妨把\(score_a-score_b\)压入转移方程，则\(A\)的目的是求\(score_a-score_b\)极大化，而\(B\)的目的是求\(score_a-score_b\)极小化，这就是\(max-min\)对抗式搜索模型。

我们再来分析一下每一步的状态：一个格子可以落子当且仅当这个格子内没有棋子且这个格子的左侧及上方的所有格子内都有棋子，题目中这样一句话给了我们一个轮廓线描述状态的启示，我们只能在这样的轮廓线上进行，用0描述竖着的轮廓线，用1描述横着的轮廓线，则状态可以被长为\(n+m\)的轮廓线唯一的表示

画图举个例子

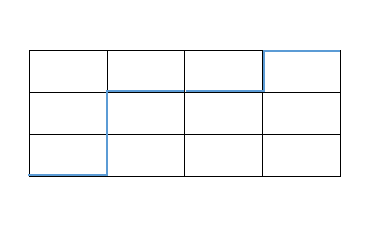
轮廓线为1001101

当进行状态转移时，我们模拟一下可以发现，当某位上为1而这一位的更高一位上为0时，当我们把这两位取反就是把轮廓线向外扩张了一个。用轮廓线确定坐标也不难，我们从低位开始枚举，对每一位的0或1决定如何移动当前对应坐标即可

---

Code：

#include <cstdio>
const int inf=0x3f3f3f3f;
int max(int x,int y){return x>y?x:y;}
int min(int x,int y){return x<y?x:y;}
int n,m,a[12][12],b[12][12],dp[1048578],used[1048578];
void init()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&b[i][j]);
}
int dfs(int s,int who)
{
    if(used[s])
        return dp[s];
    used[s]=1;
    dp[s]=who?-inf:inf;
    int x=1,y=m,tmp;
    for(int i=0;i<n+m-1;i++)
    {
        if(((s>>i)&1)&&!((s>>i+1)&1))
        {
            tmp=s^(3<<i);
            if(who)
                dp[s]=max(dp[s],dfs(tmp,who^1)+a[x][y]);
            else
                dp[s]=min(dp[s],dfs(tmp,who^1)-b[x][y]);
        }
        if((s>>i)&1) y--;
        else x++;
    }
    return dp[s];
}
int main()
{
    init();
    used[(1<<n+m)-(1<<n)]=1;
    printf("%d\n",dfs((1<<m)-1,1));
    return 0;
}

---

2018.7.6