leetcode-爬楼梯(动态规划）

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶
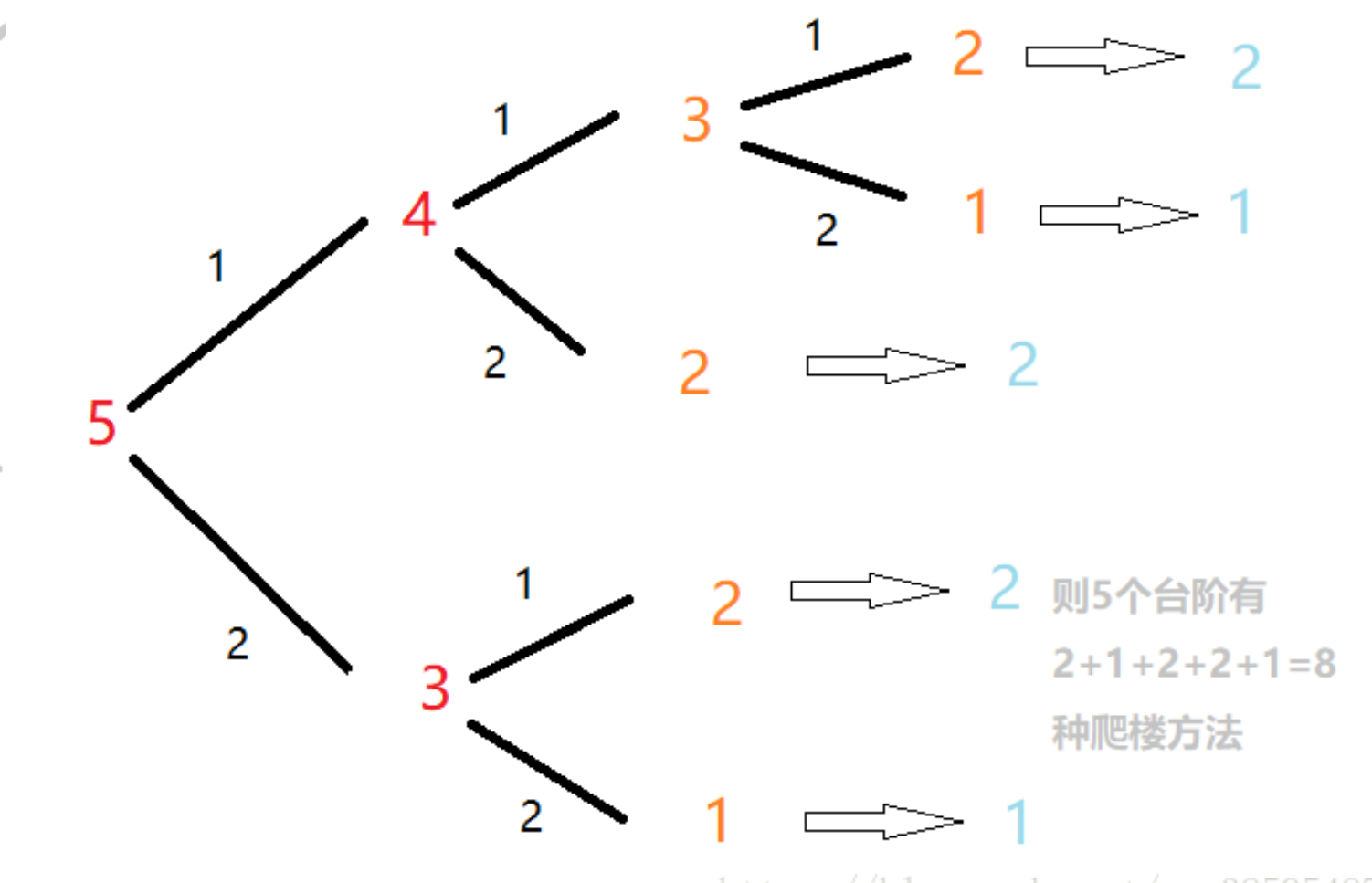
思路：可以这样想，n个台阶，一开始可以爬 1 步，也可以爬 2 步，那么n个台阶爬楼的爬楼方法就等于 一开始爬1步的方法数 + 一开始爬2步的方法数，这样我们就只需要计算n-1个台阶的方法数
和n-2个台阶方法数，同理，计算n-1个台阶的方法数只需要计算一下n-2个台阶和n-3个台阶，计算n-2个台阶需要计算一下n-3个台阶和n-4个台阶……

class Solution {
    public int climbStairs(int n) {
        if(n==1)return 1;
        int sum[]=new int[n+1];
        sum[0]=0;sum[1]=1;sum[2]=2;
     for(int i=3;i<=n;i++){
         sum[i]=sum[i-2]+sum[i-1];
     }
        return sum[n];
    }
}