poj1681 Painter's Problem（高斯消元法，染色问题）

题意：

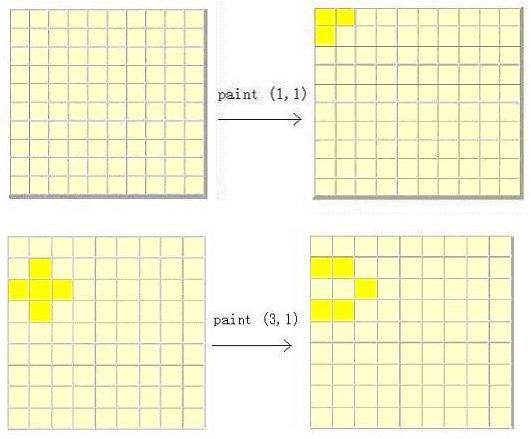
一个n*n 的木板 ，每个格子 都 可以 染成 白色和黄色，（ 一旦我们对也个格子染色 ，他的上下左右都将改变颜色）；

给定一个初始状态 ， 求将 所有的 格子 染成黄色 最少需要染几次？  若 不能 染成 输出 inf。

高斯消元，写得很懵逼。慢慢理解orz。

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 #include<string>
 #define Inf 0x3fffffff
 #define maxn 300
 using namespace std;
 int n;
 int a[maxn][maxn];  //增广矩阵
 int x[maxn];   //解集
 int free_x[maxn];   //标记是否为不确定的变元
 void init(){
     memset(a,,sizeof(a));
     memset(x,,sizeof(x));
     memset(free_x,,sizeof(free_x));
     for (int i=;i<n;i++){
         for (int j=;j<n;j++){
             int t=i*n+j;
             a[t][t]=;
             if (i>) a[(i-)*n+j][t]=;
             if (i<n-) a[(i+)*n+j][t]=;
             if (j>) a[i*n+j-][t]=;
             if (j<n-) a[i*n+j+][t]=;
         }
     }
 }
 // 高斯消元法解方程组(Gauss-Jordan elimination).(-2表示有浮点数解，但无整数解，
 //-1表示无解，0表示唯一解，大于0表示无穷解，并返回自由变元的个数)
 //有equ个方程，var个变元。增广矩阵行数为equ,分别为0到equ-1,列数为var+1,分别为0到var.
 int Gauss(int equ,int var){
     for (int i=;i<=var;i++){
         x[i]=;
         free_x[i]=;
     }
     int i,j,k,num=;
     int now=;//当前处理的列
     for (k=;k<equ && now<var;k++,now++){  //枚举行
         int max_r=k;
         for (i=k+;i<equ;i++){
             if (abs(a[i][now])>abs(a[max_r][now])) max_r=i;
         }
         if (max_r!=k){//与第i行交换
             for (j=k;j<=var;j++) swap(a[k][j],a[max_r][j]);
         }
         if (a[k][now]==){// 说明该now列第k行以下全是0了，则处理当前行的下一列.
             k--;
             free_x[num++]=now;
             continue;
         }
         for (i=k+;i<equ;i++){
             if (a[i][now]!=){
                 for (j=now;j<=var;j++){
                     a[i][j]^=a[k][j];
                 }
             }
         }
     }
     // 1. 无解的情况: 化简的增广阵中存在(0, 0, ..., a)这样的行(a != 0).
     for (i=k;i<equ;i++){
         // 对于无穷解来说，如果要判断哪些是自由变元，那么初等行变换中的交换就会影响，则要记录交换.
         if (a[i][now]!=) return -;
     }
     int stat=<<(var-k); //自由变元有 var-k 个
     int res=Inf;
     for (i=;i<stat;i++){ //枚举所有变元
         int cnt=,index=i;
         for (j=;j<var-k;j++){
             x[free_x[j]]=(index&);
             if (x[free_x[j]]) cnt++;
             index>>=;
         }
         for (j=k-;j>=;j--){
             int tmp=a[j][var];
             for (int l=j+;l<var;l++){
                 if (a[j][l]) tmp^=x[l];
             }
             x[j]=tmp;
             if (x[j]) cnt++;
         }
         if (cnt<res) res=cnt;
     }
     return res;
 }
 int main(){
     int t;
     cin >> t;
     string str;
     while (t--){
         cin >> n;
         init();
         for (int i=;i<n;i++){
             cin >> str;
             for (int j=;j<n;j++){
                 if (str[j]=='y') a[i*n+j][n*n]=;
                 else a[i*n+j][n*n]=;
             }
         }
         int k=Gauss(n*n,n*n);
         if (k==-) cout << "inf\n";
         else cout << k << endl;
     }
     return ;
 }