CF1060C Maximum Subrectangle【乘法分配律】【最大子矩阵】

CF1060C Maximum Subrectangle

题意翻译

现在给出一个长度为N的a数列,一个长度为M的b数列. 现在需要构造出一个矩阵c,其中ci,j​=ai​×bj​.再给出一个x,请在矩阵中找出一个最大的矩形,使得这个矩形中的所有值的和小于等于x.

题目描述

You are given two arrays aa and bb of positive integers, with length n and m respectively.

Let c be an n×m matrix, where ci,j​=ai​⋅bj​ .

You need to find a subrectangle of the matrix c such that the sum of its elements is at most x , and its area (the total number of elements) is the largest possible.

Formally, you need to find the largest number s such that it is possible to choose integers x1​,x2​,y1​,y2​ subject to n1≤x1​≤x2​≤n , m1≤y1​≤y2​≤m , (x2​−x1​+1)×(y2​−y1​+1)=s , and $\sum_{i=x_1}^{x2}{\sum_{j=y_1}^{y2}{c{i,j}}} \leq x.$

输入输出格式

输入格式：

The first line contains two integers n and m ( 1≤n,m≤2000 ).

The second line contains n integers a1​,a2​,…,an​ ( 1≤ai​≤2000 ).

The third line contains m integers b1​,b2​,…,bm​ ( 1≤bi​≤2000 ).

The fourth line contains a single integer x ( 1≤x≤2⋅109 ).

输出格式：

If it is possible to choose four integersx1​,x2​,y1​,y2​ such that n1≤x1​≤x2​≤n ,  m1≤y1​≤y2​≤m , and x∑i=x1​x2​​∑j=y1​y2​​ci,j​≤x , output the largest value of (x2​−x1​+1)×(y2​−y1​+1) among all such quadruplets, otherwise output 0 .

输入输出样例

输入样例#1： 复制

3 3
1 2 3
1 2 3
9

输出样例#1： 复制

4

输入样例#2： 复制

5 1
5 4 2 4 5
2
5

输出样例#2： 复制

1

说明

Matrix from the first sample and the chosen subrectangle (of blue color):

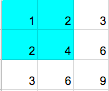
Matrix from the second sample and the chosen subrectangle (of blue color):

---

Solution

没想到是道水题QAQ

可以发现，一个子矩阵的值实际上就是这个子矩阵包括的$a$和$b$数组的乘积，根据乘法分配律可得。

所以可以预处理出长度一定时最小的$a、b$区间，然后双指针扫描即可。

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#define LL long long
using namespace std;

int n, m;
LL a[], b[], x;
LL suma[], sumb[], ans, maa[], mab[];

int main() {
    memset(maa, 0x3f3f3f3f, sizeof(maa));
    memset(mab, 0x3f3f3f3f, sizeof(mab));
    scanf("%d%d", &n, &m);
    for(int i = ; i <= n; i ++) {
        scanf("%lld", &a[i]);
        suma[i] = suma[i - ] + a[i];
        for(int j = ; j <= i; j ++)
            maa[j] = min(maa[j], suma[i] - suma[i - j]);
    }
    for(int i = ; i <= m; i ++) {
        scanf("%lld", &b[i]);
        sumb[i] = sumb[i - ] + b[i];
        for(int j = ; j <= i; j ++)
            mab[j] = min(mab[j], sumb[i] - sumb[i - j]);
    }
    scanf("%lld", &x);
    LL j = ;
    for(LL i = m; i >= ; i --) {
        while(j < n && maa[j + ] * mab[i] <= x)
            j ++;
        ans = max(ans, j * i);
    }
    printf("%lld", ans);
    return ;
}