AtCoder Grand Contest 019 F-yes or no

AtCoder Grand Contest 019 F-yes or no

解题思路：

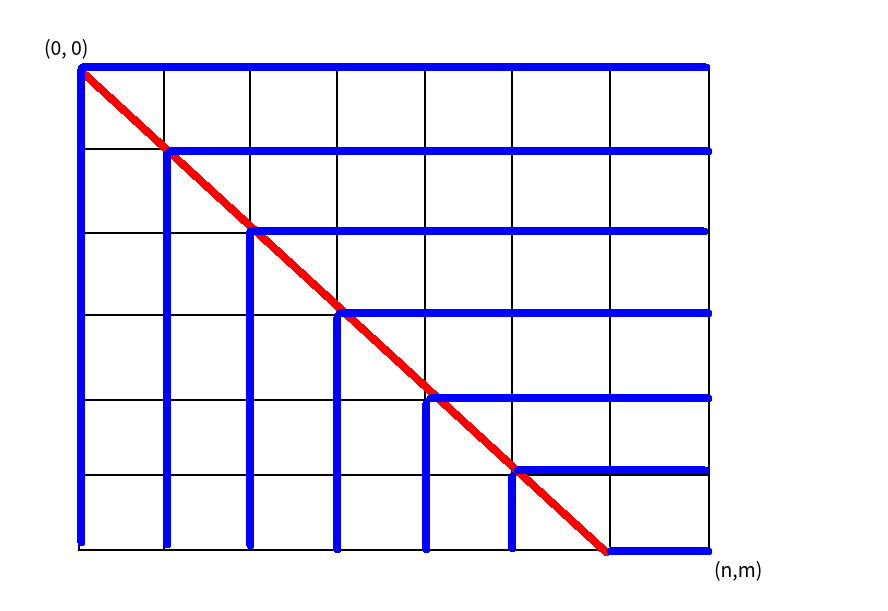
考虑一个贪心策略，假设当前还有 \(x\) 道 \(\text{yes}\) 和 \(y\) 道 \(\text{no}\) ，那么一定猜较大者，如果 \(x=y\) 就相当于随便猜一个，把 \((x, y)\) 用坐标表示，把所有在这种决策下猜对的边用蓝色表示，走过这样一条边就相当于有 \(1\) 的贡献，然后会发现从 \((0,0)\) 到 \((n,m)\) 的所有路径经过的蓝色的边的数量都是相同的 \(\max(n,m)\) 条，也就是说只需要考虑每次在 \((x=y)\) 时的决策的贡献之和就好了。

这个东西就是经过这个点的路径方案数乘上 \(\dfrac{1}{2}\) ，组合数搞搞就好了

code

/*program by mangoyang*/
#pragma GCC optimize("Ofast", "inline")
#include <bits/stdc++.h>
#define inf (0x7f7f7f7f)
#define Max(a, b) ((a) > (b) ? (a) : (b))
#define Min(a, b) ((a) < (b) ? (a) : (b))
typedef long long ll;
using namespace std;
template <class T>
inline void read(T &x){
	int f = 0, ch = 0; x = 0;
	for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = 1;
	for(; isdigit(ch); ch = getchar()) x = x * 10 + ch - 48;
	if(f) x = -x;
}
const int N = 1000005, mod = 998244353;
ll js[1000005], inv[1000005], n, m, ans;
inline ll Pow(ll a, ll b){
	ll ans = 1;
	for(; b; b >>= 1, a = a * a % mod)
		if(b & 1) ans = ans * a % mod;
	return ans;
}
inline ll C(ll x, ll y){ return js[x] * inv[y] % mod * inv[x-y] % mod; }
int main(){
	read(n), read(m);
	if(n > m) swap(n, m);
	js[0] = inv[0] = 1;
	for(int i = 1; i < N; i++)
		js[i] = 1ll * js[i-1] * i % mod, inv[i] = Pow(js[i], mod - 2);
	for(int i = 1; i <= n; i++)
		(ans += C(n + m - 2 * i, m - i) * C(2 * i, i) % mod) %= mod;
	cout << ((m + ans * inv[2] % mod * Pow(C(n + m, n), mod - 2) % mod) % mod + mod) % mod << endl;
}