哈密顿图哈密顿回路哈密顿通路(Hamilton)

本文链接:http://www.cnblogs.com/Ash-ly/p/5452580.html

概念:

　　哈密顿图:图G的一个回路,若它通过图的每一个节点一次,且仅一次,就是哈密顿回路.存在哈密顿回路的图就是哈密顿图.哈密顿图就是从一点出发,经过所有的必须且只能一次,最终回到起点的路径.图中有的边可以不经过,但是不会有边被经过两次.

　　与欧拉图的区别:欧拉图讨论的实际上是图上关于边的可行便利问题,而哈密顿图的要求与点有关.

判定:

一:Dirac定理(充分条件)

　　设一个无向图中有N个顶点,若所有顶点的度数大于等于N/2,则哈密顿回路一定存在.(N/2指的是⌈N/2⌉,向上取整)

二:基本的必要条件

　　设图G=<V, E>是哈密顿图,则对于v的任意一个非空子集S,若以|S|表示S中元素的数目,G-S表示G中删除了S中的点以及这些点所关联的边后得到的子图,则W(G-S)<=|S|成立.其中W(G-S)是G-S中联通分支数.

三:竞赛图(哈密顿通路)

　　N(N>=2)阶竞赛图一点存在哈密顿通路.

算法:

一:在Dirac定理的前提下构造哈密顿回路

过程:

　　1:任意找两个相邻的节点S和T,在其基础上扩展出一条尽量长的没有重复结点的路径.即如果S与结点v相邻,而且v不在路径S -> T上,则可以把该路径变成v -> S -> T,然后v成为新的S.从S和T分别向两头扩展,直到无法继续扩展为止,即所有与S或T相邻的节点都在路径S -> T上.

　　2:若S与T相邻,则路径S -> T形成了一个回路.

　　3:若S与T不相邻,可以构造出来一个回路.设路径S -> T上有k+2个节点,依次为S, v1, v2, ..., vk, T.可以证明存在节点vi(i属于[1, k]),满足vi与T相邻,且vi+1与S相邻.找到这个节点vi,把原路径变成S -> vi -> T -> vi+1 -> S,即形成了一个回路.

　　4:到此为止,已经构造出来了一个没有重复节点的的回路,如果其长度为N,则哈密顿回路就找到了.如果回路的长度小于N,由于整个图是连通的,所以在该回路上,一定存在一点与回路之外的点相邻.那么从该点处把回路断开,就变回了一条路径,同时还可以将与之相邻的点加入路径.再按照步骤1的方法尽量扩展路径,则一定有新的节点被加进来.接着回到路径2.

证明:

　　可利用鸽巢原理证明.

伪代码:

　　设s为哈密顿回路的起始点,t为哈密顿回路中终点s之前的点.ans[]为最终的哈密顿回路.倒置的意思指的是将数组对应的区间中数字的排列顺序方向.

　　1:初始化,令s = 1,t为s的任意一个邻接点.

　　2:如果ans[]中元素的个数小于n,则从t开始向外扩展,如果有可扩展点v,放入ans[]的尾部,并且t=v,并继续扩展,如无法扩展进入步骤3.

　　3:将当前得到的ans[]倒置,s和t互换,从t开始向外扩展,如果有可扩展点v,放入ans[]尾部,并且t=v,并继续扩展.如无法扩展进入步骤4.

　　4:如果当前s和t相邻,进入步骤5.否则,遍历ans[],寻找点ans[i],使得ans[i]与t相连并且ans[i +１]与ｓ相连,将从ans[i + 1]到t部分的ans[]倒置,t=ans[i +１],进如步骤5.

　　5:如果当前ans[]中元素的个数等于n,算法结束,ans[]中保存了哈密顿回路(可看情况是否加入点s).否则,如果s与t连通,但是ans[]中的元素的个数小于n,则遍历ans[],寻找点ans[i],使得ans[i]与ans[]外的一点(j)相连,则令s=ans[i - 1],t = j,将ans[]中s到ans[i - 1]部分的ans[]倒置,将ans[]中的ans[i]到t的部分倒置,将点j加入到ans[]的尾部,转步骤2.

时间复杂度:

　　如果说每次到步骤5算一轮的话,那么由于每一轮当中至少有一个节点被加入到路径S -> T中,所以总的轮数肯定不超过n轮,所以时间复杂度为O(n^2).空间上由于边数非常多,所以采用邻接矩阵来存储比较适合.

代码:

 const int maxN = 1;

 inline void reverse(int arv[maxN + ], int s, int t){//将数组anv从下标s到t的部分的顺序反向

     int temp;

     while(s  < t){

         temp = arv[s];

         arv[s] = arv[t];

         arv[t] = temp;

         s++;

         t--;

     }

 }

 void Hamilton(int ans[maxN + ], bool map[maxN + ][maxN + ], int n){

     int s = , t;//初始化取s为1号点

     int ansi = ;

     int i, j;

     int w;

     int temp;

     bool visit[maxN + ] = {false};

     for(i = ; i <= n; i++) if(map[s][i]) break;

     t = i;//取任意邻接与s的点为t

     visit[s] = visit[t] = true;

     ans[] = s;

     ans[] = t;

     while(true){

         while(true){//从t向外扩展

             for(i = ; i <= n; i++){

                 if(map[t][i] && !visit[i]){

                     ans[ansi++] = i;

                     visit[i] = true;

                     t = i;

                     break;

                 }

             }

             if(i > n) break;

         }

         w = ansi - ;//将当前得到的序列倒置,s和t互换,从t继续扩展,相当于在原来的序列上从s向外扩展

         i = ;

         reverse(ans, i, w);

         temp = s;

         s = t;

         t = temp;

         while(true){//从新的t继续向外扩展,相当于在原来的序列上从s向外扩展

             for(i = ; i <= n; i++){

                 if(map[t][i] && !visit[i]){

                     ans[ansi++] = i;

                     visit[i] = true;

                     t = i;

                     break;

                 }

             }

             if(i > n) break;

         }

         if(!map[s][t]){//如果s和t不相邻,进行调整

             for(i = ; i < ansi - ; i++)//取序列中的一点i,使得ans[i]与t相连,并且ans[i+1]与s相连

                 if(map[ans[i]][t] && map[s][ans[i + ]])break;

             w = ansi - ;

             i++;

             t = ans[i];

             reverse(ans, i, w);//将从ans[i +１]到ｔ部分的ans[]倒置

         }//此时s和t相连

         if(ansi == n) return;//如果当前序列包含n个元素,算法结束

         for(j = ; j <= n; j++){//当前序列中元素的个数小于n,寻找点ans[i],使得ans[i]与ans[]外的一个点相连

             if(visit[j]) continue;

             for(i = ; i < ansi - ; i++)if(map[ans[i]][j])break;

                 if(map[ans[i]][j]) break;

         }

         s = ans[i - ];

         t = j;//将新找到的点j赋给t

         reverse(ans, , i - );//将ans[]中s到ans[i-1]的部分倒置

         reverse(ans, i, ansi - );//将ans[]中ans[i]到t的部分倒置

         ans[ansi++] = j;//将点j加入到ans[]尾部

         visit[j] = true;

     }

 }

二:N(N>=2)阶竞赛图构造哈密顿通路

N阶竞赛图:含有N个顶点的有向图,且每对顶点之间都有一条边.对于N阶竞赛图一定存在哈密顿通路.

数学归纳法证明竞赛图在n >= 2时必存在哈密顿路:

(1)n = 2时结论显然成立；

(2)假设n = k时,结论也成立,哈密顿路为V1, V2, V3, ..., Vk;

设当n = k+1时,第k + 1个节点为V(k+1),考虑到V(k+1)与Vi(1<=i<=k)的连通情况,可以分为以下两种情况.

1:Vk与V(k+1)两点之间的弧为<Vk, V(k+1)>,则可构造哈密顿路径V1, V2,…, Vk, V(k+1).

2:Vk与V(k+1)两点之间的弧为<V(k+1),Vk>,则从后往前寻找第一个出现的Vi(i=k-1,i>=1,--i),满足Vi与V(k+1)之间的弧为<Vi,V(k+1)>,则构造哈密顿路径V1, V2, …, Vi, V(k+1), V(i+1), …, V(k).若没找到满足条件的Vi,则说明对于所有的Vi(1<=i<=k)到V(k+1)的弧为<V(k+1),V(i)>,则构造哈密顿路径V(k+1), V1, V2, …, Vk.

证毕.

竞赛图构造哈密顿路时的算法同以上证明过程.

Normal
0

7.8 磅
0
2

false
false
false

EN-US
ZH-CN
X-NONE

/* Style Definitions */
table.MsoNormalTable
{mso-style-name:普通表格;
mso-tstyle-rowband-size:0;
mso-tstyle-colband-size:0;
mso-style-noshow:yes;
mso-style-priority:99;
mso-style-parent:"";
mso-padding-alt:0cm 5.4pt 0cm 5.4pt;
mso-para-margin:0cm;
mso-para-margin-bottom:.0001pt;
mso-pagination:widow-orphan;
font-size:10.5pt;
mso-bidi-font-size:11.0pt;
font-family:等线;
mso-ascii-font-family:等线;
mso-ascii-theme-font:minor-latin;
mso-fareast-font-family:等线;
mso-fareast-theme-font:minor-fareast;
mso-hansi-font-family:等线;
mso-hansi-theme-font:minor-latin;
mso-font-kerning:1.0pt;}

用图来说明:

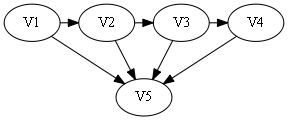
假设此时已经存在路径V1 -> V2 -> V3 -> V4,这四个点与V5的连通情况有16种,给定由0/1组成的四个数,第i个数为0代表存在弧<V5,Vi>,反之为1,表示存在弧<Vi,V5>

Normal
0

7.8 磅
0
2

false
false
false

EN-US
ZH-CN
X-NONE

sign[]={0, 0, 0, 0}.

很显然属于第二种情况,从后往前寻找不到1,即且不存在弧<Vi, V5>.

则构造哈密顿路:V5 -> V1 -> V2 -> V3 -> V4.

Normal
0

7.8 磅
0
2

false
false
false

EN-US
ZH-CN
X-NONE

sign[]={0, 0, 0, 1}.

属于第一种情况,最后一个数字为1,即代表存在弧<Vi, V5>且i=4(最后一个点)

则构造哈密顿路: V1 -> V2 -> V3 -> V4 -> V5.

Normal
0

7.8 磅
0
2

false
false
false

EN-US
ZH-CN
X-NONE

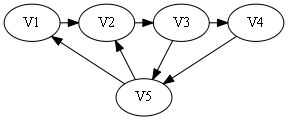
sign[]={0, 0, 1, 0}.

属于第二种情况,从后往前找到1出现的第一个位置为3.

构造哈密顿路: V1 -> V2 -> V3 -> V5 -> V4.

Normal
0

7.8 磅
0
2

false
false
false

EN-US
ZH-CN
X-NONE

sign[]={0, 0, 1, 1}.

属于第一种情况,最后一个数字为1,即代表存在弧<Vi, V5>且i=4(最后一个点)

则构造哈密顿路: V1 -> V2 -> V3 -> V4 -> V5.

Normal
0

7.8 磅
0
2

false
false
false

EN-US
ZH-CN
X-NONE

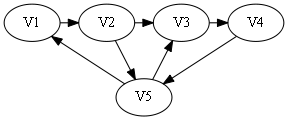
sign[]={0, 1, 0, 0}.

属于第二种情况,从后往前找到1出现的第一个位置为2.

构造哈密顿路: V1 -> V2 -> V5 -> V3-> V4.

Normal
0

7.8 磅
0
2

false
false
false

EN-US
ZH-CN
X-NONE

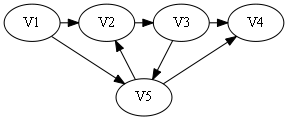
sign[]={0, 1, 0, 1}.

属于第一种情况,最后一个数字为1,即代表存在弧<Vi, V5>且i=4(最后一个点)

则构造哈密顿路:V1 -> V2 -> V3 -> V4 -> V5.(就不举末尾为1的栗子了~~)

Normal
0

7.8 磅
0
2

false
false
false

EN-US
ZH-CN
X-NONE

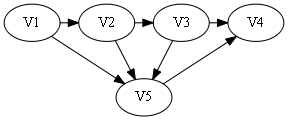
sign[]={1, 0, 1, 0}.

属于第二种情况,从后往前找到1出现的第一个位置为3.

构造哈密顿路: V1 -> V2 -> V3 -> V5-> V4.

Normal
0

7.8 磅
0
2

false
false
false

EN-US
ZH-CN
X-NONE

sign[]={1, 1, 1, 0}.

属于第二种情况,从后往前找到1出现的第一个位置为3.

构造哈密顿路: V1 -> V2 -> V3 -> V5-> V4.

Normal
0

7.8 磅
0
2

false
false
false

EN-US
ZH-CN
X-NONE

(还是举一个吧~~~)

sign[]={1, 1, 1, 1}.

同样最后一位为1,代表存在<Vi, V5>且i=4(最后一位)

则构造哈密顿路:V1 -> V2 -> V3 -> V4 -> V5.以上是当N=4时(N+1=5),用图来阐述算法的过程.

注意从后往前找不是找这个点编号之前的点,即不是按照编号来的,而是按照当前哈密顿序列从后往前找的.举个栗子:

2 1

1 3

3 2

4 1

4 2

4 3

第一步ans={1}

第二步ans={2,1}

第三步sign={0, 1}(map[3][2] = 0,map[3][1] = 1,当前序列为2,1) ,而不是{1, 0}(1,2),因为存在弧<V1, V3>和<V3, V2>.这里需要注意下.

代码:

 #include <iostream>

 #include <cmath>

 #include <cstdio>

 #include <cstring>

 #include <cstdlib>

 #include <algorithm>

 #include <queue>

 #include <stack>

 #include <vector>

 using namespace std;

 typedef long long LL;

 const int maxN = ;

 //The arv[] length is len, insert key befor arv[index]

 inline void Insert(int arv[], int &len, int index, int key){

     if(index > len) index = len;

     len++;

     for(int i = len - ; i >= ; --i){

         if(i != index && i)arv[i] = arv[i - ];

         else{arv[i] = key; return;}

     }

 }

 void Hamilton(int ans[maxN + ], int map[maxN + ][maxN + ], int n){

     int ansi = ;

     ans[ansi++] = ;

     for(int i = ; i <= n; i++){//第一种情况,直接把当前点添加到序列末尾

         if(map[i][ans[ansi - ]] == )

             ans[ansi++] = i;

         else{

             int flag = ;

             for(int j = ansi - ; j > ; --j){//在当前序列中,从后往前找到第一个满足条件的点j,使得存在<Vj,Vi>且<Vi, Vj+1>.

                 if(map[i][ans[j]] == ){//找到后把该点插入到序列的第j + 1个点前.

                     flag = ;

                     Insert(ans, ansi, j + , i);

                     break;

                 }

             }

             if(!flag)Insert(ans, ansi, , i);//否则说明所有点都邻接自点i,则把该点直接插入到序列首端.

         }

     }

 }

 int main()

 {

     //freopen("input.txt", "r", stdin);

     int t;

     scanf("%d", &t);

     while(t--){

         int N;

         scanf("%d", &N);

         int M = N * (N - ) / ;

         int map[maxN + ][maxN + ] = {};

         for(int i = ; i < M; i++){

             int u, v;

             scanf("%d%d", &u, &v);

             //map[i][j]为1说明j < i,且存在弧<Vi, Vj>,因为插入时只考虑该点之前的所有点的位置,与之后的点没有关系.所以只注重该点与其之前的点的连通情况.

             if(u < v)map[v][u] = ;

         }

         int ans[maxN + ] = {};

         Hamilton(ans, map, N);

         for(int i = ; i <= N; i++)

             printf(i ==  ? "%d":" %d", ans[i]);

         printf("\n");

     }

     return ;

 }

代码2:

 void Hamilton(int ans[maxN + ], int map[maxN + ][maxN + ], int n){

     int nxt[maxN + ];

     memset(nxt, -, sizeof(nxt));

     int head = ;

     for(int i = ; i <= n; i++){

         if(map[i][head]){

             nxt[i] = head;

             head = i;

         }else{

             int pre = head, pos = nxt[head];

             while(pos != - && !map[i][pos]){

                 pre = pos;

                 pos = nxt[pre];

             }

             nxt[pre] = i;

             nxt[i] = pos;

         }

     }

     int cnt = ;

     for(int i = head; i != -; i = nxt[i])

         ans[++cnt] = i;

 }

代码三:

 void Hamitton(bool reach[N + ][N + ], int n)

 {

     vector <int> ans;

     ans.push_back();

     for(int i=;i <= n;i++)

     {

         bool cont = false;

         for(int j=;j<(int)ans.size()-;j++)

             if(reach[ ans[j] ][i] && reach[i][ ans[j+] ])

             {

                 ans.insert(ans.begin()+j+,i);

                 cont = true;

                 break;

             }

         if(cont)

             continue;

         if(reach[ ans.back() ][i])

             ans.push_back(i);

         else

             ans.insert(ans.begin(),i);

     }

     for(int i=;i<n;i++)

                    printf("%d%c",ans[i],i==n-?'\n':' ');

 }

Normal
0

7.8 磅
0
2

false
false
false

EN-US
ZH-CN
X-NONE

哈密顿图哈密顿回路哈密顿通路(Hamilton)的更多相关文章

ZOJ 3332 Strange Country II (竞赛图构造哈密顿通路)
链接:http://www.icpc.moe/onlinejudge/showProblem.do?problemCode=3332 本文链接:http://www.cnblogs.com/Ash-l ...
POJ 1776 Task Sequences(竞赛图构造哈密顿通路)
链接:http://poj.org/problem?id=1776 本文链接:http://www.cnblogs.com/Ash-ly/p/5458635.html 题意: 有一个机器要完成一个作业 ...
hdu 5424 Rikka with Graph II (BestCoder Round #53 (div.2))(哈密顿通路判断）
http://acm.hdu.edu.cn/showproblem.php?pid=5424 哈密顿通路:联通的图,访问每个顶点的路径且只访问一次 n个点n条边 n个顶点有n - 1条边,最后一条边的 ...
POJ 2438 哈密顿回路
Children's Dining Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 4730 Accepted: 754 ...
判断是否存在哈密顿路--HDU 5424
题意:给一张无向图,判断是否是哈密顿图. 哈密顿路:经过每个点有且仅有一次的一条通路. 方法:每次找度数最小的点作为起点,然后dfs整个图,看能遍历到的点的数目能否达到n. #include<i ...
POJ 1780 Code（有向图的欧拉通路）
输入n(1<=n<=6),输出长度为10^n + n -1 的字符串答案. 其中,字符串以每n个为一组,使得所有组都互不相同,且输出的字符串要求字典序最小. 显然a[01...(n-1)] ...
HDU1116 Play on Words（有向图欧拉通路）
我把单词当作点,然后这样其实是不对的,这样就要判定是否是哈密顿通路.. 这题应该把单词的首尾单词当作点,而单词本身就是边,那样就是判定欧拉通路了. 有向图包含欧拉通路的充要条件是:首先基图连通,然后是 ...
今日SGU 5.27
SGU 122 题意:给你n个人,每个人有大于 N / 2(向上取整)的朋友,问你1这个人有一个书,每个人都想看,只能从朋友之间传递,然后最后回到了1这个人,问你是否有解,然后有解输出路径收获:哈 ...
ACM模板_axiomofchoice
目录语法 c++ java 动态规划多重背包最长不下降子序列计算几何向量(结构体) 平面集合基本操作二维凸包旋转卡壳最大空矩形 | 扫描法平面最近点对 | 分治最小圆覆盖 | 随机 ...

随机推荐

2018软工实践—Beta冲刺(1)
队名火箭少男100 组长博客林燊大哥作业博客 Beta 冲鸭! 成员冲刺阶段情况林燊(组长) 过去两天完成了哪些任务协调组内工作调试服务器性能展示GitHub当日代码/文档签入记录(组内 ...
新手向：Vue 2.0 的建议学习顺序
新手向:Vue 2.0 的建议学习顺序尤雨溪 1 年前注:2.0 已经有中文文档 .如果对自己英文有信心,也可以直接阅读英文文档.此指南仅供参考,请根据自身实际情况灵活调整.欢迎转载,请注明出 ...
Python3.6 AES加密 pycrypto‎ 更新为 pycrypto‎demo | TypeError: Object type <class 'str'> cannot be passed to C code
#!/usr/bin/env python# -*- coding:utf-8 -*-# @author: rui.xu# @update: jt.huang# 这里使用pycrypto‎demo库# ...
IPV6 简单验证
1. 网络路由器的分类 .通常将网络中直接面向用户连接或访问网络的部分称为接入层,接入层目的是允许终端用户连接到网络,因此接入层交换机具有低成本和高端口密度特性: .将位于接入层和核心层之间的部分称为 ...
本地存储—localStorage（HTML5）
https://my.oschina.net/jgy/blog/99631 localStorage简介今夜死活睡不着,决定整理下最近搞得localStorage…… 先简单说下阐述下:localS ...
latex添加eps文档
latex添加图像时,要将.eps文档放在当前文件夹中,然后使用: % For one-column wide figures use\begin{figure}\begin{center}% Use ...
hdu6447 YJJ's Salesman
这个题意和数据范围一看就是离散化之后树状数组优化DP.给的"从左下方走上去才能拿到收益"的性质其实可以当成"必须从横纵坐标严格比某个点小的地方转移过来".1A了 ...
QML——添加自定义模块
一.模块的定义在使用QML时,我们常常看到类似这样的语句: import QtQuick 2.0 import QtSensors 5.0 通过这些import语句,我们就能使用QML中的相关控件了 ...
jenkins 通过maven部署Tomcat8报错
问题过程 jenkins执行构建过程中,可以在workspace/项目名/target/目录下产生xxx.jar文件但是在执行构建后操作时报出如下错误 [INFO] ---------------- ...
hao123劫持主页
转自:https://www.zhihu.com/question/39881858 第一步 Firefox.打开Firefox,按Alt+H弹出帮助菜单,点“故障排除信息” 第二步点“配置文件夹” ...

哈密顿图 哈密顿回路 哈密顿通路(Hamilton)

哈密顿图 哈密顿回路 哈密顿通路(Hamilton)的更多相关文章

随机推荐

热门专题

哈密顿图哈密顿回路哈密顿通路(Hamilton)

哈密顿图哈密顿回路哈密顿通路(Hamilton)的更多相关文章