hmm学习笔记（二）

学习hmm近一周的时间，做个总结。

参考  李航的《统计学习方法》第9章，第10章

本文包含：

1.hmm模型

2.前向后向算法

3.Baum-Welch算法

4.维特比算法

1.hmm模型

Q：所有可能的状态的集合（一般是指隐藏状态），N是指可能的状态数

V：所有可能的观测的集合，M是可能的观测数

I：长度为T的状态序列。（一般是指隐藏状态），T是时间

O：对应的观测序列。和I一样的时间T，表明一一对应。

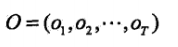
A：状态转移概率矩阵

　　　　　　(A=[a_{ij}]_{N*N})

　　　　(a_{ij}=P(i_{t+1}=q_{j}|i_{t}=q_{i}),i=1,2,...,N;j=1,2,...,N)

aij是指时刻t处于状态qi的条件下在时刻t+1转移到状态qj的概率。（上一时刻状态i，转移到下一时刻状态j的概率）

B：观测概率矩阵

　　        (B=[b_{j}(k)]_{N*M})

　　        (b_{j}(k)=P(o_{t}=v_{k}|i_{t}=q_{j}),k=1,2,...,M;j=1,2,...,N)

bj(k)指在时刻t处于状态qj的条件下，生成观测为vk的概率。（状态为j，生成观测为k的概率）

pai：初始状态概率向量

　　　　　　(\pi =(\pi_{i}))

　　　　　　\pi_{i}=P(i_{1}=q_{i}),i=1,2,...,N

pai(i)时刻t=1处于状态qi的概率。（初始时刻的状态也是不确定的，也可能是各个状态的分布）

hmm模型参数：可由pai，A，B构成，pai和A决定状态序列，B决定观测序列。hmm模型用lambda表示：

　　　　　　(\lambda =(A,B,\pi ))

2.问题一:概率计算问题

给定hmm模型，和观测序列O，计算在模型lambda下观测序列O出现的概率

2.1前向算法

前向概率：给定hmm，定义到时刻 t 观测序列为 {o1,o2...ot}，且状态为qi的概率。

　　　　　　(\alpha _{t}(i)=P(o_{1},o_{2},...,o_{t},i_{t}=q_{i}|\lambda ))

（已知观测序列o，t 时刻状态为 i 的前向概率 ）

初值：

递归：

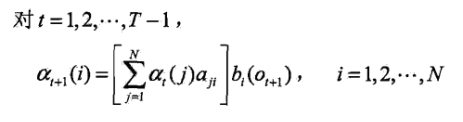
理解一下：

• 　　  　　  (\alpha _{t}(j)*a_{ji})     时刻 t 观测到o1,o2...ot，并在 t 时刻处于状态 qj ，而在时刻t+1状态为 qi 的联合概率
• 　　   (\sum_{j=1}^{N}\alpha _{t}(j)*a_{ji})     对所有状态 qj 求和，时刻 t 观测到o1,o2...ot，并在时刻t+1状态为 qi 的联合概率，这一步可以认为是：到t+1状态为qi的前一时刻所有的概率之和。类似下面这个图。

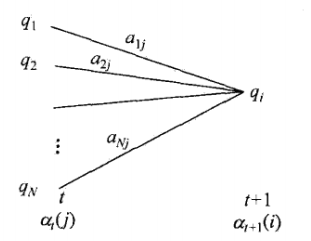
• 　　   （\sum_{j=1}^{N}\alpha _{t}(j)*a_{ji}*b_{i}(o_{t+1})）  时刻t+1观测到o1,o2...ot+1，且状态为qi ，对比前向概率的定义，可得出此结果即为

终止：

     T时刻，所有的状态都加起来（跟状态 i 无关了，也即跟隐藏状态无关了）

2.2后向算法

后向概率：给定hmm，时刻 t，状态为qi 的条件下，从t+1到T的观测为{ot+1,...,oT}的概率

　　　　　　(\beta _{t}(i)=P(o_{t+1},o_{t+2},...,o_{T}|i_{t}=q_{i},\lambda ))

（时刻 t 状态为 i 的情况下，从t+1到T的观测到ot+1....oT的概率，叫后向概率）

初值：

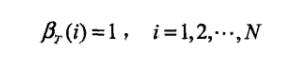
递归：

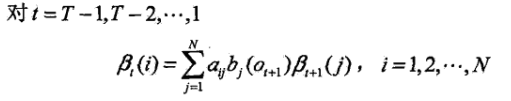
欲求，可以先看其与，下一时刻的关系

，时刻t+1状态为 j，从t+2到T的观测为ot+2...oT的概率。

比较一下这两个，就知道，只需要把 t+1 到 t+2 段的概率求出即可，t+2到T是重复的 ，即可用表示

第一种理解：

　　  　　上一时刻状态 i 转移到下一时刻 j 的概率

　　　　上一时刻状态 i ，下一时刻状态 j ，且在状态 j 的条件下，观测为 ot+1的联合概率，注意，这时候要结合，这表示状态  j 观察到ot+2... oT的概率

　　    上一时刻状态 i ，下一时刻状态 j ，且在状态 j 的条件下，观测到ot+1,ot+2...oT的概率

　　所有状态 j 相加，就跟 j 无关了，类似下面的图

　　　　上一时刻状态为 i ，下一时刻观测到ot+1,ot+2...oT的概率

　　对比一下定义即可得：

　　     　　\beta  _{t}(i)=\sum_{j=1}^{N}a_{ij}*b_{j}(o_{t+1})*\beta _{t+1}(j)

第二种理解：

　　　　　　状态为 j ，观测为ot+2，...，oT的概率

　　　　　　状态为 j ，观测为ot+1，ot+2...oT的概率

　　　　上一时刻状态为 i ，下一时刻状态为 j ，且在状态 j 下观测为ot+1，ot+2...oT的联合概率

　　为什么用 aij ？　　因为要用来表示，时间上来看是后一时刻的状态 j 表示前一时刻的状态 i ，但是前一时刻的状态 i 先发生，后一时刻的状态 j 后发生

　　       这边就一样了，上一时刻状态为 i ，下一时刻观测到ot+1,ot+2...oT的概率

终止：

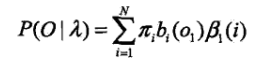
观察一下：

前向计算       T时刻，所有的状态的前向概率都加起来

  　　在模型 下观测序列 {o1,o2...oT} 出现的概率，欲求  ，前向是对进行求和，可以推测后向应该是搞

　　　　　时刻 t=1处于状态 i 的条件下，观测为o1的概率

　　　　时刻 t=1 状态为 i 观测为 {o2,o3...oT} 的概率

　　　　时刻 t=1 状态为 i 观测为 {o1,o2...oT} 的概率

　　　　　　求和，与状态 i 无关，观测为 {o1,o2...oT}的概率

即　　

前后向结合起来，可以写成一般形式：

　　

计算概率和期望：

给定模型和观测O，在时刻 t 处于状态 qi 的概率：

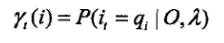
给定模型和观测O，在时刻 t 处于状态 qi ，且在时刻 t+1 处于状态 qj 的概率：

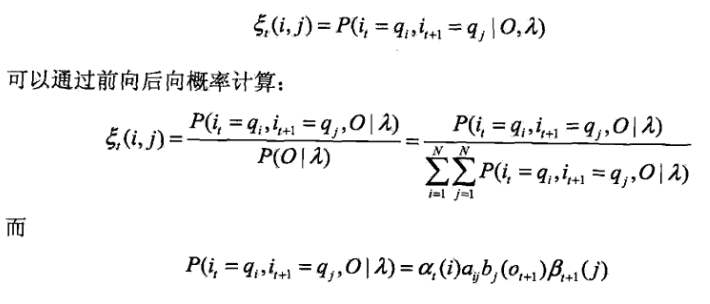
所以

后面部分的参考    隐马尔科夫模型 HMM（一）HMM 模型  ，讲的很细，还有配合的代码