2018.08.28 集合堆栈机（模拟+STL）

描述

中学数学里集合的元素往往是具体的数字，比如A = {1,2,3}，B = {}（空集）等等。但是要特别注意，集合的元素也可以是另一个集合，比如说C = {{}}，即说明C有且仅有一个元素——空集B，所以称B是C的子集或者称B是C的元素都是正确的。所谓一个集合的势，就是这个集合的元素个数，一般记为|S|，空集的势为0。在上例中，|A| = 3，|B| = 0，|C| = 1。鉴于集合论是现代数学的基础理论这一事实，一群异想天开的科学家开始着手建造一台新式的超级计算机——集合堆栈机Alpha，这台机器操作的将是集合而不是数字。不过由于Alpha的竣工之日遥遥无期，科学家们希望你为他们编写一台虚拟机，好让他们检查自己的原型设计是否合理。 Alpha的存储设备只有一个栈，栈的每个单元都只能放置一个集合。一开始，栈是空的，在每个操作结束后，计算机就会输出位于栈顶单元的那个集合的势。Alpha拥有五种不同的指令，分别为：PUSH、DUP、UNION、INTERSECT和ADD，他们的功能如下：

PUSH：把一个空集{}压入栈；

DUP：取出位于栈顶单元的集合，复制一遍以后再把两个同样的集合压入栈；

UNION：取出位于栈顶单元的前两个集合，然后把它们的并集压入栈；

INTERSECT：取出位于栈顶单元的前两个集合，然后把它们的交集压入栈；

ADD：取出位于栈顶单元的前两个集合，首先取出的记为S，其次取出的记为T，最后把T∪{S}压入栈；

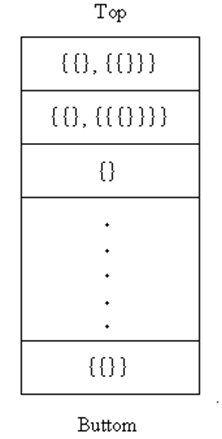
图为例，可见位于虚拟机堆栈顶端的两个元素是：

A = { {}, {{}} }

B = { {}, {{{}}} }

根据势的定义，我们有|A| = 2 以及 |B| = 2。接下来，

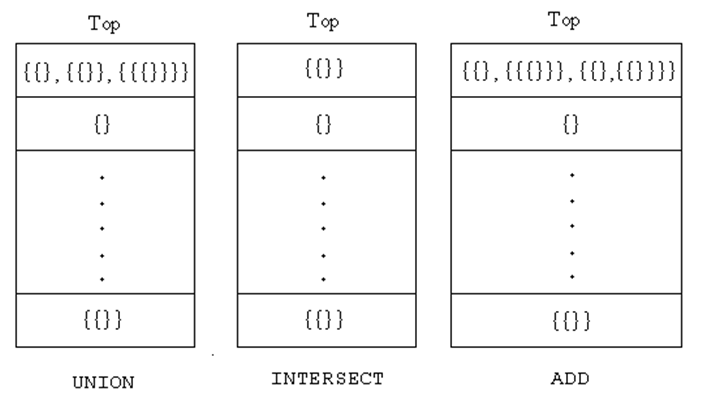
 如果选择UNION操作，结果是{{},{{}},{{{}}}，输出3

 如果选择INTERSECT操作，结果是{{}}，输出1

 如果选择ADD操作，结果是{{},{{{}}},{{},{{}}}}，输出3

分别执行三条指令之后虚拟机就会变成以下三种样子：

输入

文件的第一行只有一个整数n（0≤n≤2000），代表将要执行的指令条数。接下来有n行，每行有包含一条大写的指令，我们保证每条指令都是上述五条指令中的一条，并且虚拟机总是能正确执行完所有的指令。

输出

输出虚拟机的输出结果即可。每行输出一个大于或等于0的整数，代表虚拟机执行该条指令后的输出。选手们务必仔细考量程序的执行效率。

样例输入

9

PUSH

DUP

ADD

PUSH

ADD

DUP

ADD

DUP

UNION

样例2

5

PUSH

PUSH

ADD

PUSH

INTERSECT

样例输出

0

0

1

0

1

1

2

2

2

样例2

0

0

1

0

0

康复训练ing。。。

好吧这题显然不能直接模拟，有一种感觉很优秀的做法是将集合映射成int来乱搞。

然后写了一发感觉取交集与并集有点麻烦。。。

赶快百度了一波惊奇的发现STL中已经有了这个操作心情大好！

于是顺利跑过了。

代码：

#include<bits/stdc++.h>
using namespace std;
struct cmp{
    inline bool operator()(const set<int>&a,const set<int>b){
        if(a.size()!=b.size())return a.size()<b.size();
        set<int>::iterator ita=a.begin(),itb=b.begin();
        while(ita!=a.end()&&*ita==*itb)++ita,++itb;
        return ita==a.end()?false:(*ita<*itb);
    }
};
stack<int>stk;
map<set<int>,int,cmp>mp;
vector<set<int> >vec;
inline int findid(set<int>x){
    if(mp[x])return mp[x];
    vec.push_back(x);
    return mp[x]=vec.size()-1;
}
int main(){
    string s;
    int q;
    scanf("%d",&q);
    while(q--){
        cin>>s;
        if(s[0]=='P')stk.push(findid(set<int>()));
        else if(s[0]=='D')stk.push(stk.top());
        else{
            set<int>x1=vec[stk.top()],tmp;
            stk.pop();
            set<int>x2=vec[stk.top()];
            stk.pop();
            if(s[0]=='U')set_union(x1.begin(),x1.end(),x2.begin(),x2.end(),inserter(tmp,tmp.begin()));
            else if(s[0]=='I')set_intersection(x1.begin(),x1.end(),x2.begin(),x2.end(),inserter(tmp,tmp.begin()));
            else tmp=x2,tmp.insert(findid(x1));
            stk.push(findid(tmp));
        }
        cout<<vec[stk.top()].size()<<'\n';
    }
    return 0;
}