统计学习方法ｃ++实现之二 k近邻法

统计学习方法ｃ++实现之二 k近邻算法

前言

k近邻算法可以说概念上很简单，即：“给定一个训练数据集，对新的输入实例，在训练数据集中找到与这个实例最邻近的k个实例，这k个实例的多数属于某个类，就把该输入分为这个类。”其中我认为距离度量最关键，但是距离度量的方法也很简单，最长用的就是欧氏距离，其他的距离度量准则实际上就是不同的向量范数，这部分我就不赘述了，毕竟这系列博客的重点是实现。代码地址：https://github.com/bBobxx/statistical-learning

kd树

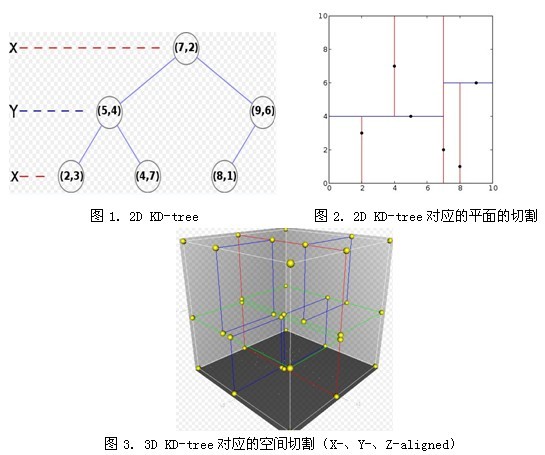
k近邻算法的思想很简单，然而，再简单的概念如果碰上高维度加上海量数据，就变得很麻烦，如果按照常规思想，将每个测试样本和训练样本的距离算出来，在进行排序查找，无疑效率十分低下，这也就是为什么要介绍kd树的原因。kd树是一种二叉树，kd树的每个结点对应一个k维超矩形区域。 kd树的k是k维空间，k近邻算法的k是k个最近值，不是一样的！看文字很抽象，其实很好理解，看图

代码结构

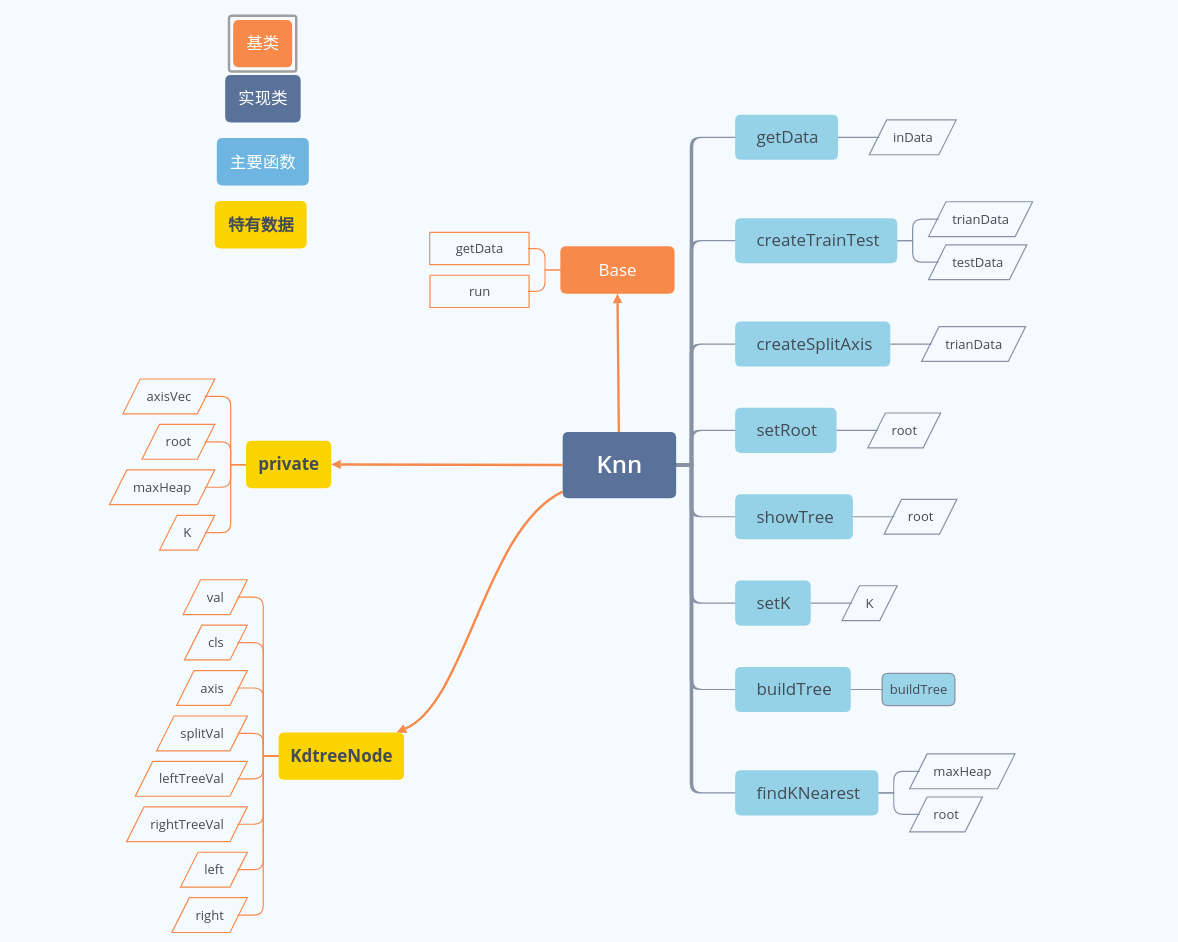
实现

kd树构建代码

每一次分割都需要确定一个轴和一个值，然后分割时只看该轴的数据，小于等于分割值就放到该结点的左子树里，大于分割值就放到右子树中。那么每个结点里面需要存储哪些内容呢？

我的实现里面，每个结点有如下内容：

struct KdtreeNode {
    vector<double> val;//n维特征
    int cls;//类别
    unsigned long axis;//分割轴
    double splitVal;//分割的值
    vector<vector<double>> leftTreeVal;//左子树的值集合
    vector<vector<double>> rightTreeVal;//右子树的值集合
    KdtreeNode* parent;//父节点
    KdtreeNode* left;//左子节点
    KdtreeNode* right;//右子节点
    KdtreeNode(): cls(0), axis(0), splitVal(0.0), parent(nullptr), left(nullptr), right(nullptr){};

};

用kd树实现的k近邻算法（还有其它的方法），训练过程实际上就是树的建造过程，我们用递归创建kd树。

首先，我们需要创建并存储根节点

KdtreeNode* root = new KdtreeNode();//类中用这个存储根节点

void Knn::setRoot() {//这是创建根节点的程序，主要是设定左右子树，还有分割轴，分割值
    if(axisVec.empty()){
        cout<<"please run createSplitAxis first."<<endl;
        throw axisVec.empty();
    }
    auto axisv = axisVec;
    auto axis = axisv.top();
    axisv.pop();
    std::sort(trainData.begin(), trainData.end(), [&axis](vector<double> &left, vector<double > &right) {
        return left[axis]<right[axis];
    });
    unsigned long mid = trainData.size()/2;
    for(unsigned long i = 0; i < trainData.size(); ++i){
        if(i!=mid){
            if (i<mid)
                root->leftTreeVal.push_back(trainData[i]);

            else
                root->rightTreeVal.push_back(trainData[i]);
        } else{
            root->val.assign(trainData[i].begin(),trainData[i].end()-1);
            root->splitVal = trainData[i][axis];
            root->axis = axis;
            root->cls = *(trainData[i].end()-1);
        }
    }
    cout<<"root node set over"<<endl;
}

上面的程序创建了根节点，但是分割轴是怎么确定？当然可以依次选轴作为分割轴，但是这里我们选择按方差从大到小的顺序选轴

stack<unsigned long> axisVec;//用栈存储分割轴，栈顶轴方差最大。

void Knn::createSplitAxis(){//axisVec创建代码
    cout<<"createSplitAxis..."<<endl;
    //the last element of trainData is gt
    vector<pair<unsigned long, double>> varianceVec;
    auto sumv = trainData[0];
    for(unsigned long i=1;i<trainData.size();++i){
        sumv = sumv + trainData[i];
    }
    auto meanv = sumv/trainData.size();
    vector<decltype(trainData[0]-meanv)> subMean;
    for(const auto& c:trainData)
        subMean.push_back(c-meanv);
    for (unsigned long i = 0; i < trainData.size(); ++i) {
        for (unsigned long j = 0; j < indim; ++j) {
            subMean[i][j] *= subMean[i][j];
        }

    }
    auto varc = subMean[0];
    for(unsigned long i=1;i<subMean.size();++i){
        varc = varc + subMean[i];
    }
    auto var = varc/subMean.size();
    for(unsigned long i=0;i<var.size()-1;++i){//here not contain the axis of gt
        varianceVec.push_back(pair<unsigned long, double>(i, var[i]));
    }
    std::sort(varianceVec.begin(), varianceVec.end(), [](pair<unsigned long, double> &left, pair<unsigned long, double> &right) {
        return left.second < right.second;
    });
    for(const auto& variance:varianceVec){
        axisVec.push(variance.first);//the maximum variance is on the top
    }
    cout<<"createSplitAxis over"<<endl;
}

现在要给根节点添加左右子树：

    root->left = buildTree(root, root->leftTreeVal, axisVec);
    root->right = buildTree(root, root->rightTreeVal, axisVec);

来看一下buildTree代码：

KdtreeNode* Knn::buildTree(KdtreeNode*root, vector<vector<double>>& data, stack<unsigned long>& axisStack) {//第一个参数是父节点，第二个参数是目前没有被分割的数据集合，第三个参数是当前的轴栈，
 //由于后面要保证左右子树的分割用的同一个轴，所以这里要传入。

    stack<unsigned long> aS;
    if(axisStack.empty())
        aS=axisVec;
    else
        aS=axisStack;
    auto node = new KdtreeNode();
    node->parent = root;

    auto axis2 = aS.top();
    aS.pop();

    std::sort(data.begin(), data.end(), [&axis2](vector<double> &left, vector<double > &right) {
        return left[axis2]<right[axis2];
    });//这里用的c++11里面的lambda函数

    unsigned long mid = data.size()/2;

    if(node->leftTreeVal.empty()&&node->rightTreeVal.empty()){
        for(unsigned long i = 0; i < data.size(); ++i){
            if(i!=mid){
                if (i<mid)
                    node->leftTreeVal.push_back(data[i]);
                else
                    node->rightTreeVal.push_back(data[i]);

            } else{
                node->val.assign(data[i].begin(),data[i].end()-1);
                node->splitVal = data[i][axis2];
                node->axis = axis2;
                node->cls = *(data[i].end()-1);
            }
        }
    }

    if(!node->leftTreeVal.empty()){
        node->left = buildTree(node, node->leftTreeVal, aS);//递归建立子树
    }
    if(!node->rightTreeVal.empty()){
        node->right = buildTree(node, node->rightTreeVal, aS);
    }

    return node;
}

建立好子树后可以通过showTree函数前序遍历树来查看，这里就不演示了，代码中有这一步。

查找K近邻

对于用kd树实现的Knn算法来说，预测的过程就是查找的过程，这里我们给出查找K个最近邻的代码，中间用到了STL标准模板库的priority_queue和pair的组合，用priority_queue实现大顶堆，对于由pair构成的priority_queue来说，默认的比较值是first,也就是说里面的元素会根据pair的第一个元素从大到小排序，即用.top()得到的是最大值（默认比较函数的情况下）。在搜索 K-近邻时，设置一个有 k 个元素的大顶堆，建立树时，当堆不满时，将结点和距离放入，堆满时，只需比较当前搜索点的 dis 是否小于堆顶点的 dis，如果小于，堆顶出堆，并将当前搜索点压入。

priority_queue<pair<double, KdtreeNode*>> maxHeap;

下面给出查找代码

void Knn::findKNearest(vector<double>& testD){
        ...//前面略过，避免代码过长。。。
        if(testDF[curNparent->axis]<=curNparent->splitVal)//从这里开始是为了查找同一个父节点的
            										   //另一个子树中是否有比当前K个最近邻更近的结点
            curNchild = curNparent->right;//这里和上面相反，刚好是另一个子树。
        else
            curNchild = curNparent->left;
        if(curNchild == nullptr)
            continue;
        double childDis = computeDis(testDF, curNchild->val);
        if(childDis<maxHeap.top().first){//比较另一个子树的根节点是不是比当前k个结点距离查找点更近，
            						   //如果是，将对应的子树加入搜索路径
            maxHeap.pop();
            maxHeap.push(pair<double, KdtreeNode*>(childDis, curNchild));
            while(curNchild!= nullptr){//add subtree to path
                path.push(curNchild);
                if(testD[curNchild->axis]<=curNchild->splitVal)
                    curNchild = curNchild->left;
                else
                    curNchild = curNchild->right;
            }
        }
    }

}

double Knn::computeDis(const vector<double>& v1, const vector<double>& v2){
    auto v = v1 - v2;
    double di = v*v;//这里用到了基类中的操作符重载
    return di;
}

总结

k近邻算法虽然概念简单，但是实现由于要用到树结构，编写起来还是挺具有挑战性的，以后还会进行性能的优化，慢慢来。