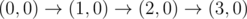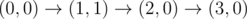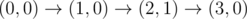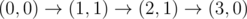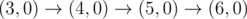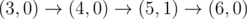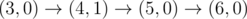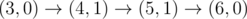Codeforces 821E Okabe and El Psy Kongroo（矩阵快速幂）

E. Okabe and El Psy Kongroo

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Okabe likes to take walks but knows that spies from the Organization could be anywhere; that's why he wants to know how many different walks he can take in his city safely. Okabe's city can be represented as all points (x, y) such that x and y are non-negative. Okabe starts at the origin (point (0, 0)), and needs to reach the point (k, 0). If Okabe is currently at the point (x, y), in one step he can go to (x + 1, y + 1), (x + 1, y), or (x + 1, y - 1).

Additionally, there are n horizontal line segments, the i-th of which goes from x = ai to x = bi inclusive, and is at y = ci. It is guaranteed that a1 = 0, an ≤ k ≤ bn, and ai = bi - 1 for 2 ≤ i ≤ n. The i-th line segment forces Okabe to walk with y-value in the range 0 ≤ y ≤ ci when his xvalue satisfies ai ≤ x ≤ bi, or else he might be spied on. This also means he is required to be under two line segments when one segment ends and another begins.

Okabe now wants to know how many walks there are from the origin to the point (k, 0) satisfying these conditions, modulo 109 + 7.

Input

The first line of input contains the integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 1018) — the number of segments and the destination xcoordinate.

The next n lines contain three space-separated integers ai, bi, and ci (0 ≤ ai < bi ≤ 1018, 0 ≤ ci ≤ 15) — the left and right ends of a segment, and its y coordinate.

It is guaranteed that a1 = 0, an ≤ k ≤ bn, and ai = bi - 1 for 2 ≤ i ≤ n.

Output

Print the number of walks satisfying the conditions, modulo 1000000007 (109 + 7).

Examples

input

1 3
0 3 3

output

4

input

2 6
0 3 0
3 10 2

output

4

Note

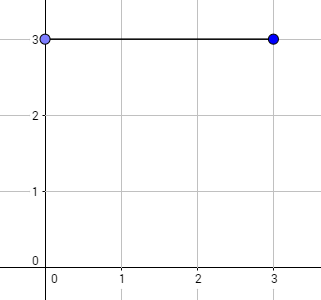
The graph above corresponds to sample 1. The possible walks are:

• 
• 
• 
• 

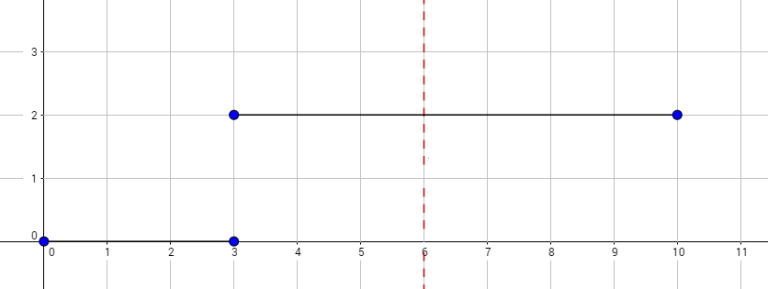
The graph above corresponds to sample 2. There is only one walk for Okabe to reach (3, 0). After this, the possible walks are:

• 
• 
• 
• 

题目链接：CF 821E

很好的一道题，用dp[x][y]表示到坐标$(x,y)$的方案数，容易可以想到简单的递推：$dp[x][y]=dp[x-1][y]+dp[x-1][y-1]+dp[x-1][y+1]$，但是由于x太大不能直接写dp，看这个式子，发现当前的dp[x]只跟dp[x-1]有关系，因此实际上只需要两个一维数组就可以完成这种迭代，那如何加速迭代呢？用矩阵快速幂，把dp[x-1][y]放到矩阵A的第一行，dp[x][y]显然是转移之后的矩阵A的第一行，如何转移？y从上一次的y-1,y+1,y进行转移，因此构造中间矩阵B，B[i][j]=i走到j是否可行，然后一条线段一条线段地进行转移，当上一次转移线段的高度为3，当前线段高度为2，那显然3这个高度已经越界了，因此转移之前要把A矩阵的越界位置方案数置0，然后用当前的高度作为行数进行转移，否则会多算，最后注意一下长度不能超过k，不然也会多算

代码：

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <bitset>
#include <string>
#include <stack>
#include <cmath>
#include <queue>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
#define fin(name) freopen(name,"r",stdin)
#define fout(name) freopen(name,"w",stdout)
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define FAST_IO ios::sync_with_stdio(false);cin.tie(0);
typedef pair<int, int> pii;
typedef long long LL;
const double PI = acos(-1.0);
const int N = 110;
const int M = 16;
const LL mod = 1000000007LL;
int row;
struct Mat
{
    LL A[M][M];
    void zero()
    {
        CLR(A, 0);
    }
    Mat operator*(Mat b)
    {
        Mat c;
        c.zero();
        for (int i = 0; i < row; ++i)
        {
            for (int k = 0; k < row; ++k)
            {
                if (A[i][k])
                {
                    for (int j = 0; j < row; ++j)
                    {
                        if (b.A[k][j])
                            c.A[i][j] = (c.A[i][j] + A[i][k] * b.A[k][j]) % mod;
                    }
                }
            }
        }
        return c;
    }
    friend Mat operator^(Mat a, LL b)
    {
        Mat r;
        r.zero();
        for (int i = 0; i < row; ++i)
            r.A[i][i] = 1;
        while (b)
        {
            if (b & 1)
                r = r * a;
            a = a * a;
            b >>= 1;
        }
        return r;
    }
};
LL a[N], b[N];
int c[N];

int main(void)
{
    int n, i, j;
    LL k;
    while (~scanf("%d%I64d", &n, &k))
    {
        for (i = 0; i < n; ++i)
            scanf("%I64d%I64d%d", &a[i], &b[i], &c[i]);
        if (b[n - 1] > k)
            b[n - 1] = k;
        Mat A,B;
        A.zero();
        A.A[0][0] = 1;
        B.zero();
        for (j = 0; j <= 15; ++j) //列
        {
            B.A[j][j] = 1;
            if (j - 1 >= 0)
                B.A[j][j - 1] = 1;
            if (j + 1 <= 15)
                B.A[j][j + 1] = 1;
        }
        for (i = 0; i < n; ++i)
        {
            row = c[i] + 1;
            for (j = c[i] + 1; j < M; ++j)
                A.A[0][j] = 0;
            A = A * (B ^ (b[i] - a[i]));
        }
        printf("%I64d\n", A.A[0][0]);
    }
    return 0;
}