五校联考模拟赛Day2T2矩阵(容斥原理)

题意

$n * m$的网格，对其进行黑白染色，问每一行每一列至少有一个黑格子的方案数。

Sol

考场上只会$n^3$的dp，还和指数级枚举一个分qwq

设$f[i][j]$表示到了第$i$行，已经有$j$列被染黑，然后暴力转移上一行有几个黑格子

正解是容斥

首先固定好列，也就是保证每一列都有一个黑格子

这样的方案是$(2^N - 1) ^M$

然后容斥行

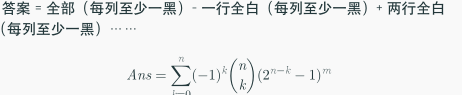
组合数暴力算即可

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<vector>
#include<set>
#include<queue>
#include<cmath>
#include<iostream>
#define Pair pair<int, int>
#define MP(x, y) make_pair(x, y)
#define fi first
#define se second
#define int long long
#define LL long long
//#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1<<22, stdin), p1 == p2) ? EOF : *p1++)
//char buf[(1 << 22)], *p1 = buf, *p2 = buf;
using namespace std;
const int MAXN = 1e6 + , INF = 1e9 + , mod = 1e9 + ;
const double eps = 1e-;
inline int read() {
    char c = getchar(); int x = , f = ;
    while(c < '' || c > '') {if(c == '-') f = -; c = getchar();}
    while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
    return x * f;
}
int N, M;
LL fac[MAXN], ifac[MAXN], po2[MAXN];
LL fastpow(int a, int p) {
    LL base = ;
    while(p) {
        if(p & ) base = (base * a) % mod;
        a = (a * a) % mod; p >>= ;
    }
    return base % mod;
}
LL C(int N, int M) {
    return fac[N] * ifac[M] % mod * ifac[N - M] % mod;
}
main() {
    N =  * 1e5;
    fac[] = ; po2[] = ;
    for(int i = ; i <= N; i++) fac[i] = i * fac[i - ] % mod, po2[i] = (po2[i - ] * ) % mod;
    ifac[N] = fastpow(fac[N], mod - );
    for(int i = N; i >= ; i--)
        ifac[i - ] = (ifac[i] % mod * i) % mod;
    N = read(); M = read();
    int d = ; LL ans = ;
    for(int i = ; i <= N; i++, d *= -)
        ans = (ans + d * C(N, i) * fastpow((po2[N - i] -  + mod) % mod, M) % mod + mod) % mod;
    cout << ans;
    return ;
}