【Foreign】石子游戏 [博弈论]

石子游戏

Time Limit: 10 Sec  Memory Limit: 256 MB

Description

　　

Input

　　

Output

　　输出T行，表示每组的答案。

Sample Input

　　3
　　1
　　1
　　2
　　1
　　0 0
　　3
　　1 2 2
　　4 4 4 4

Sample Output

　　1
　　0
　　6

HINT

　　

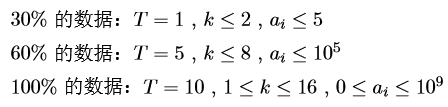
Solution

　　这显然是一道博弈论的题目。我们发现这是一个树结构，仔细看了一下，发现这显然是一个阶梯Nim的模型。

　　我们将所有和同n奇偶的值XOR起来就可以得到SG。我们先判断一下，若SG=0则显然必败，否则必胜。

　　然后我们开始计算方案，枚举每一个节点，目标显然就是要让SG=0。

　　由于XOR的消去率，根据题意，可以分 2 种情况分别讨论：（根据SG异或值判断是加入还是取出。）

　　1. 从父亲那加入值，显然就是需要 ( SG^a[这个点] ) - a[这个点的父亲] <= a[这个点]，这样才可以通过加入若干个值使得SG=0；
　　2. 把值给儿子，显然需要 (SG^a[这个点]) <= a[这个点]，这样才可以通过拿走若干的值使得SG=0。

　　然后我们讨论一下是否为叶子节点：

　　1. 非叶节点，若从父亲那加入值只有1的贡献，把值给儿子（由于有两个儿子）所以贡献为2；
　　2. 叶子节点，从父亲那加入值或者彻底删去都显然只有1的贡献。

　　这样就可以求出方案数了。

Code

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;

 const int ONE = ;
 const int INF = ;
 const int MOD = 1e9+;

 int T;
 int n;
 int x,num;
 int a[][];
 int SG,Ans;

 int get()
 {
         int res=,Q=;    char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 void Solve()
 {
         n=get();
         SG=Ans=;
         for(int i=;i<=n;i++)
         for(int j=;j<=(<<(i-));j++)
         {
             a[i][j]=get();
             if(i%==n%)    SG ^= a[i][j];
         }
         if(!SG) {printf(""); return;}

         for(int i=;i<=n;i++)
         {
             for(int j=;j<=(<<(i-));j++)
             if(i%==n%)
             {
                 if(i!=n)
                 {
                     if( (SG^a[i][j]) <= a[i][j]) Ans+=;
                     if( (SG^a[i][j]) > a[i][j] && (SG^a[i][j]) - a[i-][(j-)/+] <= a[i][j]) Ans+=;
                 }
                 if(i==n)
                 {
                     if( (SG^a[i][j]) <= a[i][j] ) Ans++;
                     if( (SG^a[i][j]) > a[i][j] && (SG^a[i][j]) - a[i-][(j-)/+] <= a[i][j] ) Ans++;
                 }
             }
         }

         printf("%d",Ans);
 }

 int main()
 {
         T=get();
         while(T--)
             Solve(),printf("\n");
 }