POJ1659 可图性判定

Frogs' Neighborhood

Time Limit: 5000MS		Memory Limit: 10000K
Total Submissions: 10660		Accepted: 4433		Special Judge

Description

未名湖附近共有N个大小湖泊L₁, L₂, ..., L_n(其中包括未名湖)，每个湖泊L_i里住着一只青蛙F_i(1 ≤ i ≤ N)。如果湖泊L_i和L_j之间有水路相连，则青蛙F_i和F_j互称为邻居。现在已知每只青蛙的邻居数目x₁, x₂, ..., x_n，请你给出每两个湖泊之间的相连关系。

Input

第一行是测试数据的组数T(0 ≤ T ≤ 20)。每组数据包括两行，第一行是整数N(2 < N < 10)，第二行是N个整数，x₁, x₂,..., x_n(0 ≤ x_i ≤ N)。

Output

对输入的每组测试数据，如果不存在可能的相连关系，输出"NO"。否则输出"YES"，并用N×N的矩阵表示湖泊间的相邻关系，即如果湖泊i与湖泊j之间有水路相连，则第i行的第j个数字为1，否则为0。每两个数字之间输出一个空格。如果存在多种可能，只需给出一种符合条件的情形。相邻两组测试数据之间输出一个空行。

Sample Input

3
7
4 3 1 5 4 2 1
6
4 3 1 4 2 0
6
2 3 1 1 2 1

Sample Output

YES
0 1 0 1 1 0 1
1 0 0 1 1 0 0
0 0 0 1 0 0 0
1 1 1 0 1 1 0
1 1 0 1 0 1 0
0 0 0 1 1 0 0
1 0 0 0 0 0 0 

NO

YES
0 1 0 0 1 0
1 0 0 1 1 0
0 0 0 0 0 1
0 1 0 0 0 0
1 1 0 0 0 0
0 0 1 0 0 0

Source

POJ Monthly--2004.05.15 Alcyone@pku

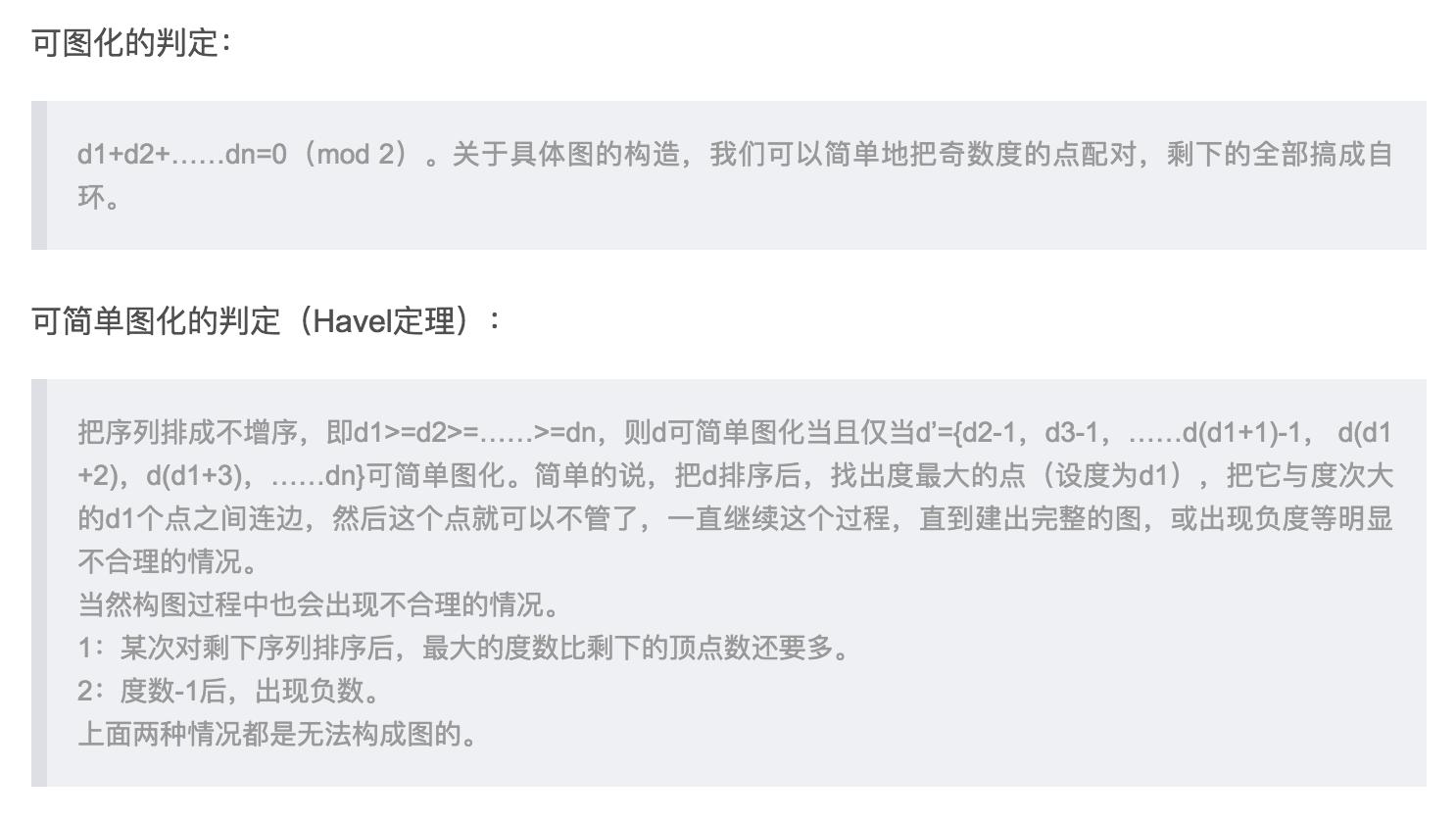
代码：

 #include"bits/stdc++.h"

 #define db double
 #define ll long long
 #define vl vector<ll>
 #define ci(x) scanf("%d",&x)
 #define cd(x) scanf("%lf",&x)
 #define cl(x) scanf("%lld",&x)
 #define pi(x) printf("%d\n",x)
 #define pd(x) printf("%f\n",x)
 #define pl(x) printf("%lld\n",x)
 #define rep(i, n) for(int i=0;i<n;i++)
 using namespace std;
 const int N = 1e6 + ;
 const int mod = 1e9 + ;
 const int MOD = ;
 const db  PI = acos(-1.0);
 const db  eps = 1e-;
 const ll  INF = 0x3fffffffffffffff;
 struct P{int id,du;};
 P a[N];
 bool cmp(P a,P b){return a.du>b.du;}
 int  t,n;
 bool s[][];
 bool cal()
 {
     memset(s,, sizeof(s));
     for(int i=;i<n;i++){
         sort(a+i,a+n,cmp);
         if(a[i].du>n-i-) return *puts("NO");
         for(int j=i+;j<=i+a[i].du;j++){
             if(!a[j].du) return *puts("NO");
             a[j].du--;
             int u=a[i].id,v=a[j].id;
             s[u][v]=,s[v][u]=;
         }
     }
     puts("YES");
     for(int i=;i<n;i++)
         for(int j=;j<n;j++) printf("%d%c",s[i][j],j==n-?'\n':' ');

     return ;
 }
 int main(){
     ci(t);
     for(int i=;i<=t;i++){
         ci(n);
         for(int i=;i<n;i++) ci(a[i].du),a[i].id=i;
         cal();
         if(i!=t) puts("");
     }
     return ;
 }