ECC椭圆曲线以及计算出公钥的过程（BTC为例）

ECC概念

全称 “ Ellipse Curve Cryptography ” means “ 椭圆曲线密码学 ”。

传统加密方法大多基于大质数因子分解困难性来实现，ECC则是通过椭圆曲线方程式的性质来产生密钥。

ECC164位的密钥产生一个安全级，相当于RSA 1024位密钥提供的保密强度，而且计算量较小，处理速度更快，存储空间和传输带宽占用较少。

应用方面：目前我国居民二代身份证正在使用 256 位的椭圆曲线密码，虚拟货币比特币也选择ECC作为加密算法。

椭圆曲线的定义以及产生公钥的过程

1 公式及图解

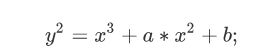
假设平面直角坐标系中有点A(x,y),我们定义 X= x/z,Y = y/z,Z=z;那么联立方程：aX+bY+c1Z =0；

aX+bY+c2Z =0 可以计算出z=0；所以我们新的坐标系中的点可以表示为：（X：Y：0）；这是椭圆曲线建立的坐标系基础。

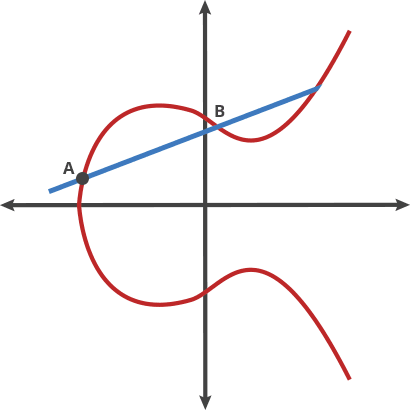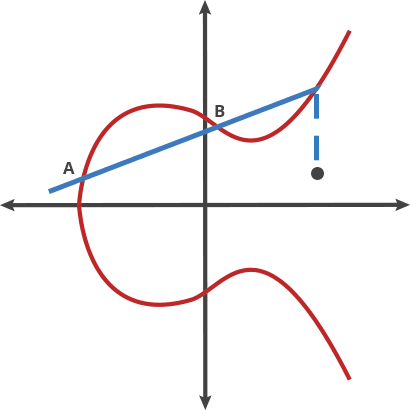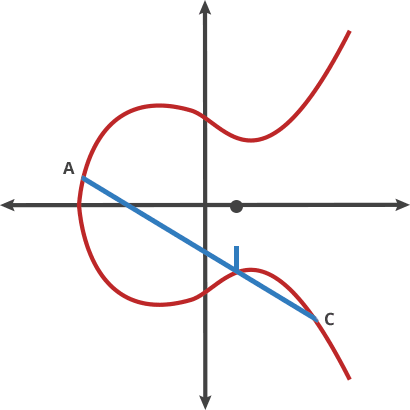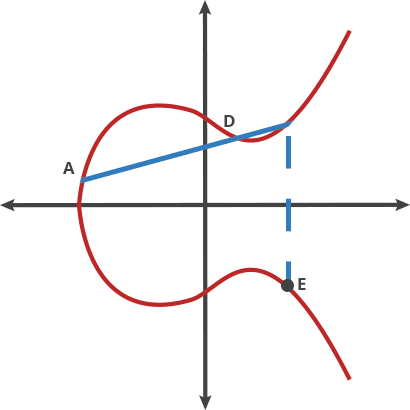
例如y^2=x^3-10x+12的曲线如下：

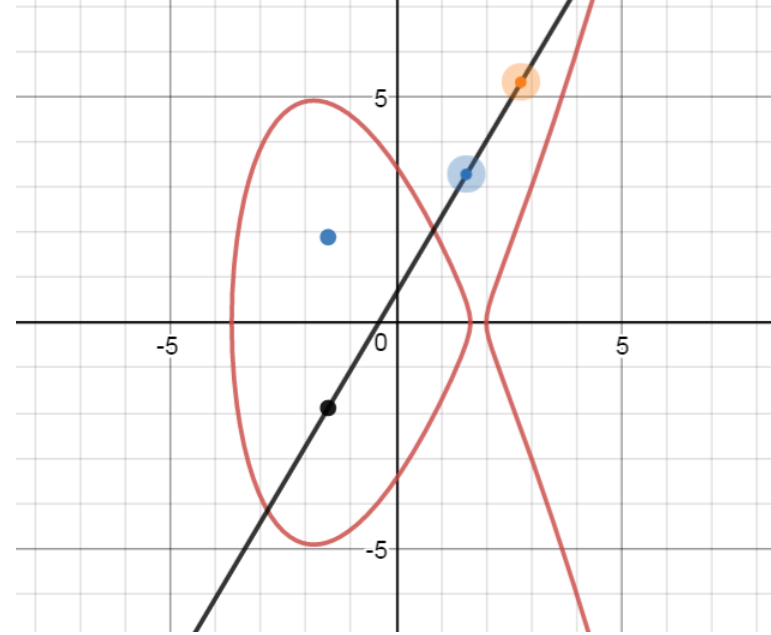
数学家在这个曲线上定义了一种椭圆曲线的加法，ECC里面的加法建立在“有限域上的二元三次曲线的点”上，组成一个“有限加法循环群”。

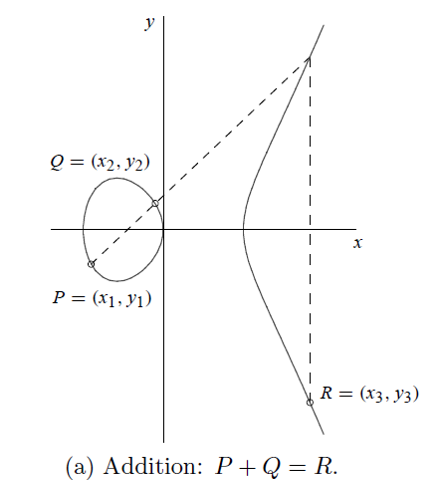
图a - 两个不同的点相加

图b - 两个相同的点相加

这并不是传统的数学上的加法，运算法则：任意取椭圆曲线上两点P、Q （若P、Q两点重合，则做P点的切线）做直线交于椭圆曲线的另一点R，过R做y轴的平行线交于R’。

我们规定P+Q=R’。所以很容易理解nP的值，就是P经过n次加法（对P做切线，取得另一个交点的关于X轴的对称点）。

2 这样定义加法的意义

（1）给使用者求逆向运算（由公钥计算私钥）的时候制造困难。
（2）为了构造一个封闭的“较好的”代数结构，简化正向运算（由私钥计算公钥的运算）。要是单纯为了求解困难，那可以定义五光十色的加法，但是加法定义的随性将导致了运算的复杂。为了能用一些最基本的运算：比如结合律、比如减法，才这么定义让这些点构成一个群。

3 如何使用这个加法呢

（1）正向计算（由私钥计算公钥）

确定椭圆曲线一个点作为基点P，由于所有的点构成一个有限群，那么基点P必然可以作为一个生成元生成一个子群。记这个子群的阶数为n，也就是说P点累加n次得到群的单位元（无穷远点），记做nP=0。（注意此处0只是一个代号，代指无穷远点，因为我们习惯了用0来表示加法单位元。）
正向计算的定义很简单，私钥为 $K\in [0,n)$ ; 基点为点 $P$ ;公钥点Q定义为 $K$ 个 $P$ 相加（也可以理解为乘法）： $Q=\underset{K}{\widehat{\underbrace{P+P+\cdots +P)}}}$ 。

（2）逆向计算（公钥反推私钥）有多难：

目前由椭圆曲线公钥求解私钥的最有效算法复杂度为 $O(\sqrt{p})$ ,其中 $p$ 是阶数 $n$ 的最大素因子。当参数选的足够好让 $p>2^{160}$ 时，以目前的计算能力，攻破椭圆曲线是不现实的。

4 产生一个公钥

有了以上的基础，我们才可以来计算公钥，产生公钥的算法其实就是椭圆曲线上的乘法运算：

Q = k * P

上面公式中，P 是椭圆曲线上的一个点，且这个点在比特币中是固定不变的；k 是我们的私钥，

我们知道私钥是一个很大的随机数；而结果 Q 就是我们产生的公钥，根据上面的知识，可以知道公钥是 k个 P 相加的结果，这个结果仍然是椭圆上的一个点

更详细资料探索：椭圆曲线公式的数学解释与参考

比特币公钥加密中使用spec256k1 标准(wiki)的椭圆曲线

$y^2 \mod{p} = (x^3+7)\mod{p}$

mod：取余符号
P：一个很大的素数
x：自变量
y：因变量

secp256k1标准通过特别的算法，使得生成曲线的速度比别的曲线快30%。这在移动端等小型设备上是非常重要的。

对于比特币中的椭圆曲线算法，需要明确知道的是(p,a,b,G,n,h)。p是Fp的模的范围，比特币中定义的是：

p = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F = 2^256 − 2^32 − 2^9 − 2^8 − 2^7 − 2^6 − 2^4 − 1。
a，b是椭圆曲线的参数，a=0，b=7。
G是基点，可以理解为椭圆曲线中第一个点，列如前面的P。比特币中定义的点G 为（02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798，483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8）。
n 是基点G的可倍积阶数，定义为能够使得点倍积nG 不存在的最小的整数n，比特币中它的值为：FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141。h是一个整数常量，它跟椭圆曲线运算中得到点的集合以及 n 有关，
h 一般取值为01。比特币中也是01。

满足下面公式的所有坐标的集合，就是spec256k1 椭圆曲线：

实际上椭圆曲线是一个散点图，并不是所有实数字x都满足这个曲线，以P=17为例子（当然了这个数很小），满足公式的（x,y）的图形：

取不同的素数，椭圆曲线会呈现出完全不同的形态，

越大，这个椭圆也就越大，可承载的数值范围也就越大，冲突率会降低，乃至于更安全。

因此比特币中采用的是一个特定的椭圆曲线，称之为 spec256k1，它是由 NIST（National Institute of Standards and Technology）这个组织确定的。

Python玩一玩

Python 3.6.7 (default, Oct 23 2018, 11:32:17)

[GCC 8.2.0] on linux

Type "help", "copyright", "credits" or "license" for more information.

# 这里取一个spec256k1的 P 的例子

>>> p = 115792089237316195423570985008687907853269984665640564039457584007908834671663

# P 可以确定一个椭圆，然后再在其中取一个点（x, y）

>>> x = 55066263022277343669578718895168534326250603453777594175500187360389116729240

>>> y = 32670510020758816978083085130507043184471273380659243275938904335757337482424

# 验证

>>> (x**3 + 7) % p  - y**2 % p

0

椭圆曲线算法安全性及其现状运用

目前椭圆曲线应用的范围越来越广，在BTC，ETH，EOS，莱特币，DASH等都有使用。密码学中把正向计算是很容易的，但若要有效的执行反向则很困难的算法叫做陷门函数。在RSA的内容里，RSA会随着因式分解的数字变大而变得越有效率，对于私钥增长的需求决定了RSA并不能算作一个完美的陷门函数。事实证明在椭圆曲线中如果你有两个点，一个最初的点乘以K次到达最终点，在你只知道最终点时找到n和最初点是很难的，这就是一个非常棒的trapdoor函数的基础，最近三十年的研究，数学家还没有找到一个方法证实。密码学家Lenstra引进了“全球安全（Global Security）”的概念：假设破解一个228字节的RSA秘钥需要的能量少于煮沸一勺水的能量。那么破解一个228字节的椭圆曲线秘钥需要煮沸地球上所有水的能量。如果RSA要达到一个同样的安全水平，你需要一个2,380字节的秘钥。就像前面文章中讲到的，ECC能够使用较小的资源而产生安全性较高的效果。

笔记参考：

https://www.cnblogs.com/gzhlt/p/10270913.html

https://www.zhihu.com/question/22399196/answer/96016340

https://www.jianshu.com/p/5040d4347c66