贝叶斯A/B测试 - 一种计算两种概率分布差异性的方法过程

1. 控制变量

0x1：控制变量主要思想

科学中对于多因素（多变量）的问题，常常采用控制因素（变量）的方法，吧多因素的问题变成多个单因素的问题。每一次只改变其中的某一个因素，而控制其余几个因素不变，从而研究被改变的这个因素对事物的影响，分别加以研究，最后再综合解决，这种方法叫控制变量法。
它是科学探索中的重要思想方法，广泛地运用在各个科学探索和科学实验研究之中。

0x2：控制变量思想在机器学习中的应用

在机器学习项目中，我们可能会将专家领域经验融合到特征工程中，即主观先验。

在设计并获得特征向量后，我们会在直方图上打印出pdf概率密度图，目的是查看不同特征之间的区分度。

这个比较过程，本质上就是控制变量过程，在该实验中，自变量是两个不同的特征，因变量是目标值（label值），其他因素都完全相同，通过对比两个不同特征的概率分布差异性（例如使用t-test），来得到特征可区分型的判断。

如果两个特征之间差异性很低，则说明可能需要进行feature selection后者feature reduction。

0x3：控制变量思想在贝叶斯统计推断中的作用

在A/B测试中，两组实验分别采用了不同的策略，其他因素完全相同，通过对实验的后验结果进行差异性分布（例如t-test），以此得到这两种策略之间是否存在明显的差异或者说增益的判断（判断本身也是概率性的）。

Relevant Link:

https://wenku.baidu.com/view/afe92b8fb04e852458fb770bf78a6529647d35c7.html

2. A/B测试简介

0x1：A/B测试基本思想

A/B测试背后的基本思想是：假如有一个理想的平行宇宙用于对照，该宇宙的人与我们这里的人是完全一样的（除控制变量外，其他变量都相同），那么此时如果给某一边的人以某种特殊的待遇（调整控制变量），那么结果所导致的变化一定会被归咎于这一特殊待遇。

但是在实践中，我们没法进入到平行宇宙，因此我们只能利用两组足够大量的样本来近似地创造一对平行宇宙。

0x2：A/B测试的最终目的

A/B测试的最终目的是比较A/B的后验分布的差异性，使用的方法有很多种，例如t-test。

0x3：A/B测试的优势

. 可解释的概率值。在贝叶斯分布中，我们可以直接回答诸如”我们出错的概率是多少“之类的问题，这在频率派的方法中通常难以回答；
. 很容易应用损失函数；

我们在这篇blog中用一个网站转化率测试的简单案例，来一起讨论下A/B测试。

Relevant Link:

https://baike.baidu.com/item/AB%E6%B5%8B%E8%AF%95/9231223?fr=aladdin

3. 二项分布问题场景的A/B测试 - 一个网站转化率测试案例

我们有A和B两种网站设计。当用户登录网站时，我们随机地将其引向其中之一（模拟随机分组），并且记录下来。当有足够多的用户访问以后，我们用得到的数据来计算两种设计的转化率指标。

考虑我们得到了如下数字：

visitors_to_A = ；
visitors_to_B = ；
conversions_from_A = ；
conversions_from_B = ；

我们关心的是A和B的转化概率。从商业化角度考虑，我们希望转化率越高越好。

为此，我们需要对A和B的转化率进行建模。

0x1：选择先验分布

由于需要对概率建模，因此选择Beta分布作为先验是一个好主意，转化率的取值范围在0~1之间。

同时，我们的访客数量和转化数据是二项式的，每个访客只有两种可能：转化 or 不转化。

Beta分布的共轭特性是的我们不需要进行MCMC，可以直接得到后验概率分布。

0x2：计算后验分布

假设我们的先验是Beta（1，1），它等价于【0，1】上的均匀分布。

输入样本数据后，得到Beta后验分布：

# -*- coding: utf- -*-

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc as pm
from scipy.stats import beta

visitors_to_A =
visitors_to_B =
conversions_from_A =
conversions_from_B = 

alpha_prior =
beta_prior = 

posterior_A = beta(alpha_prior + conversions_from_A,
                   beta_prior + visitors_to_A - conversions_from_A)

posterior_B = beta(alpha_prior + conversions_from_B,
                   beta_prior + visitors_to_B - conversions_from_B)

plt.show()

0x3：比较后验分布的大小

1. MCMC后验采样法

接下来我们想判断哪个组转化率可能更高。为此，类似MCMC的做法，我们对后验进行采样，并且比较来自于A的后验样本的概率大于来自B的后验样本的概率：

# -*- coding: utf- -*-

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc as pm
from scipy.stats import beta

visitors_to_A =
visitors_to_B =
conversions_from_A =
conversions_from_B = 

alpha_prior =
beta_prior = 

posterior_A = beta(alpha_prior + conversions_from_A,
                   beta_prior + visitors_to_A - conversions_from_A)

posterior_B = beta(alpha_prior + conversions_from_B,
                   beta_prior + visitors_to_B - conversions_from_B)

samples =
samples_posterior_A = posterior_A.rvs(samples)
samples_posterior_B = posterior_B.rvs(samples)

print(samples_posterior_A > samples_posterior_B).mean()

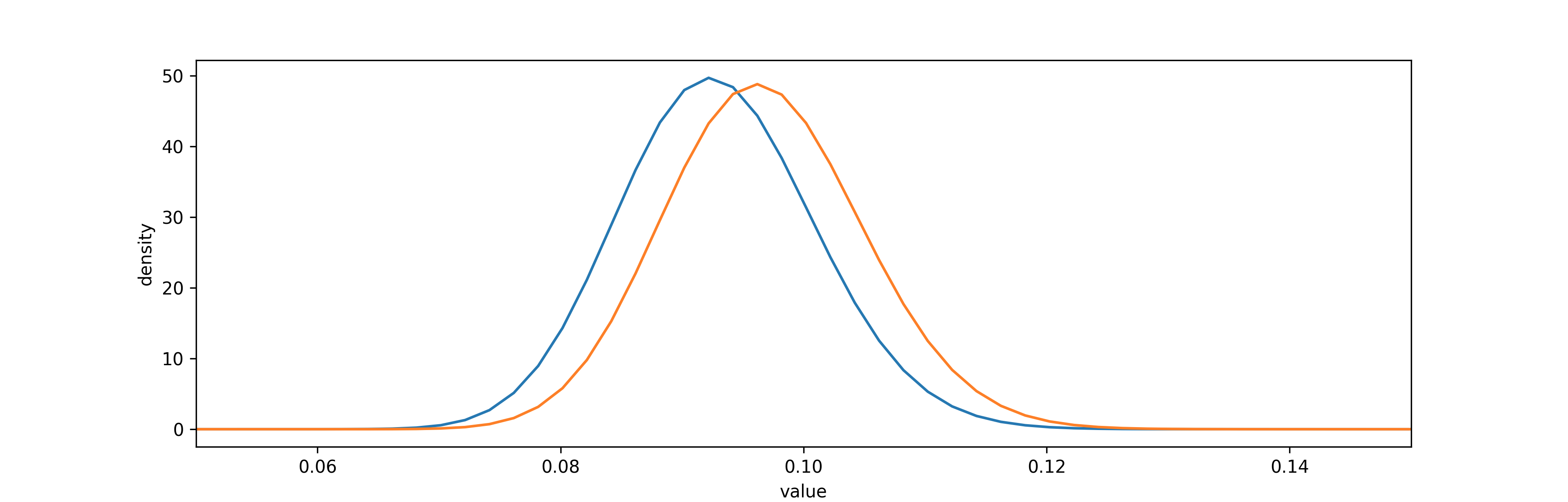
可以看到，有31%的概率A比B的转化效率高。或者说，有69%的概率B比A的转化率高。

这并不是十分显著，因为如果两个页面完全相同，那么重新实验得到的概率会接近50%，而我们实验中得出的结论比较接近50%，这个结论并不能提供多少有用的信息。

通过概率密度图显示两个分布的结果：

# -*- coding: utf- -*-

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc as pm
from scipy.stats import beta
from IPython.core.pylabtools import figsize

visitors_to_A =
visitors_to_B =
conversions_from_A =
conversions_from_B = 

alpha_prior =
beta_prior = 

posterior_A = beta(alpha_prior + conversions_from_A,
                   beta_prior + visitors_to_A - conversions_from_A)

posterior_B = beta(alpha_prior + conversions_from_B,
                   beta_prior + visitors_to_B - conversions_from_B)

samples =
samples_posterior_A = posterior_A.rvs(samples)
samples_posterior_B = posterior_B.rvs(samples)

print(samples_posterior_A > samples_posterior_B).mean()

figsize(12.5, )

plt.rcParams['savefig.dpi'] =
plt.rcParams['figure.dpi'] =
x = np.linspace(, , )
plt.plot(x, posterior_A.pdf(x), label='posterior of A')
plt.plot(x, posterior_B.pdf(x), label='posterior of B')
plt.xlim(0.05, 0.15)
plt.xlabel('value')
plt.ylabel('density')
plt.show()

2. 通过KL散度计算后验分布的差异性

Relevant Link:

https://baike.baidu.com/item/%E7%9B%B8%E5%AF%B9%E7%86%B5/4233536?fromtitle=KL%E6%95%A3%E5%BA%A6&fromid=23238109&fr=aladdin

4.  多项分布下的A/B测试

互联网公司的一个常见的目标是，不仅是要增加注册量，还要优化用户可能选择的注册方案。比如，一个业务体可能希望用户在多种备选项中，选择价格更高的方案。

假设给用户展示两个版本的定价页面，并且我们希望得到每次访问的收入期望值，不仅仅是关心用户是否注册，而是想知道能获得的收入的期望值。

0x1：收入期望的分析

企业网页总收入的期望为：

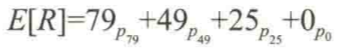
这里，P79 为选择 $79 收费方案的概率，其他的类似，$0 代表用户未选择任何收费方案（既为转化）。这样一来，整体概率和为1：

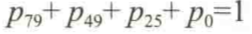
0x2：选择概率分布模型

接下来是为各个收费方案的选择先验分布。这里不能简单使用Beta分布，因为各个选项之间彼此是相关的（不符合beta分布成立条件），它们的和为1。比如，如果 P79 很大，那么其他的概率必然较小。

Beta分布有一个推广，叫做 Dirichlet（狄利克雷）分布。它返回一个和为 1 的正数数组。数组的长度由一个输入向量的长度决定，这一输入向量的值类似于先验的参数。

另一方面，对于样本数据的建模，也不能选择二项分布，因为选项不只2个。二项分布有一个推广叫做多项分布，我们的观测值服从多项分布，并且各个取值的概率都是未知的。

同时，狄利克雷分布是多项分布的共轭先验！这意味着对于位置概率的后验，我们有明确的公式。

如果先验服从 Dirichlet（1，1，...，1），并且我们的观测值为 N1，N2，....，Nm，那么后验是：

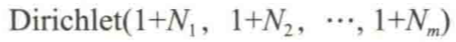
0x3：计算后验分布

假如有1000人浏览了页面，并且注册情况如下：

# -*- coding: utf- -*-

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc as pm
from numpy.random import dirichlet
from IPython.core.pylabtools import figsize

N =
N_79 =
N_49 =
N_25 =
N_0 = N - (N_79 + N_49 + N_25)

observations = np.array([N_79, N_49, N_25, N_0])

prior_parameters = np.array([, , , ])
posterior_samples = dirichlet(prior_parameters+observations, size=)

print "Two random samples from the posterior: "
print posterior_samples[]
print posterior_samples[]

for i, label in enumerate(['p_79', 'p_49', 'p_25', 'p_0']):
    ax = plt.hist(posterior_samples[:, i], bins=, label=label, histtype='stepfilled')

plt.xlabel('value')
plt.ylabel('density')
plt.show()

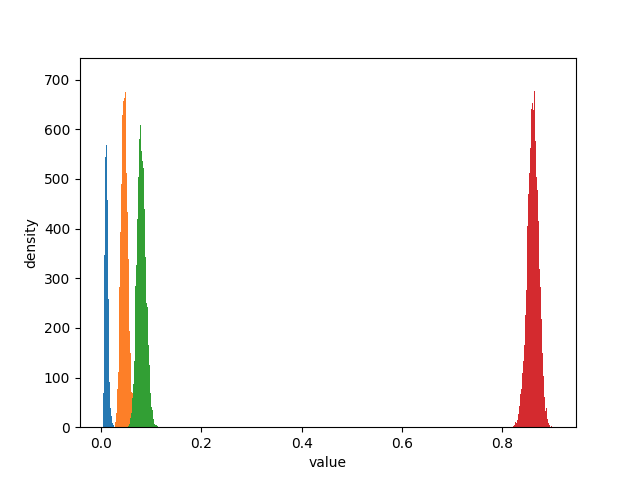
从上图可以看出，关于概率的可能取值仍然有不确定性，所有期望值的结果也是不确定的。我们得到的就是期望值的后验分布。

0x4：计算总收入期望的后验分布

来自该后验的样本的和总是1，因此可以将这些样本用于前面的期望值的公式里参与计算收入的后验期望。

# -*- coding: utf- -*-

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc as pm
from numpy.random import dirichlet
from IPython.core.pylabtools import figsize

N =
N_79 =
N_49 =
N_25 =
N_0 = N - (N_79 + N_49 + N_25)

observations = np.array([N_79, N_49, N_25, N_0])

prior_parameters = np.array([, , , ])
posterior_samples = dirichlet(prior_parameters+observations, size=)

def expected_revenue(P):
    return  * P[:, ] +  * P[:, ] +  * P[:, ] +  * P[:, ]

posterior_expected_revenue = expected_revenue(posterior_samples)

plt.hist(posterior_expected_revenue, histtype='stepfilled', label='expected revenue', bins=)
plt.xlabel('value')
plt.ylabel('density')
plt.show()

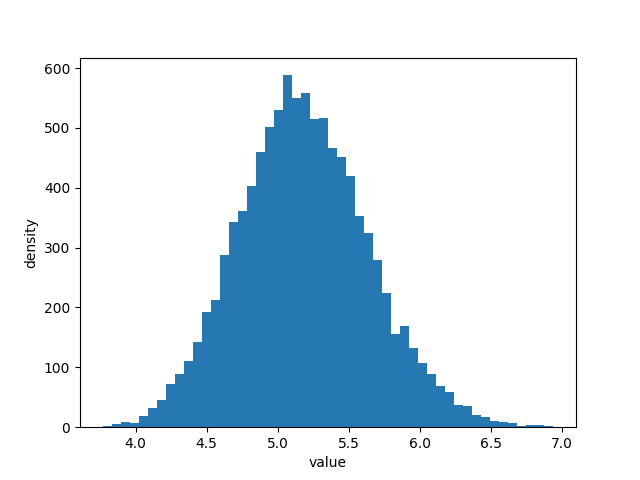
从上图中我们可以解读出几个信息：

. 收入的期望值有很大可能在 $ 和 $ 之间，不大可能在这个范围之外

0x5：对两个不同的页面进行分析 - 延伸到A/B测试

接下来我们把问题扩展一些，尝试对两个不同的WEB页面进行这样的分布，从而进行A/B测试，对比在相同的条件下，A、B页面的后验分布的概率分布差异性。

1. 计算后验分布

我们将两个站点称为A和B，并为它们虚构一些数据：

# -*- coding: utf- -*-

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc as pm
from numpy.random import dirichlet
from IPython.core.pylabtools import figsize

N_A =
N_A_79 =
N_A_49 =
N_A_25 =
N_A_0 = N_A - (N_A_79 + N_A_49 + N_A_25)
observations_A = np.array([N_A_79, N_A_49, N_A_25, N_A_0])

N_B =
N_B_79 =
N_B_49 =
N_B_25 =
N_B_0 = N_B - (N_B_79 + N_B_49 + N_B_25)
observations_B = np.array([N_B_79, N_B_49, N_B_25, N_B_0])

prior_parameters = np.array([, , , ])

posterior_samples_A = dirichlet(prior_parameters+observations_A, size=)
posterior_samples_B = dirichlet(prior_parameters+observations_B, size=)

def expected_revenue(P):
    return  * P[:, ] +  * P[:, ] +  * P[:, ] +  * P[:, ]

posterior_expected_revenue_A = expected_revenue(posterior_samples_A)
posterior_expected_revenue_B = expected_revenue(posterior_samples_B)

plt.hist(posterior_expected_revenue_A, histtype='stepfilled', label='expected revenue A', bins=)
plt.hist(posterior_expected_revenue_B, histtype='stepfilled', label='expected revenue B', bins=, alpha=0.8)

plt.xlabel('value')
plt.ylabel('density')
plt.show()

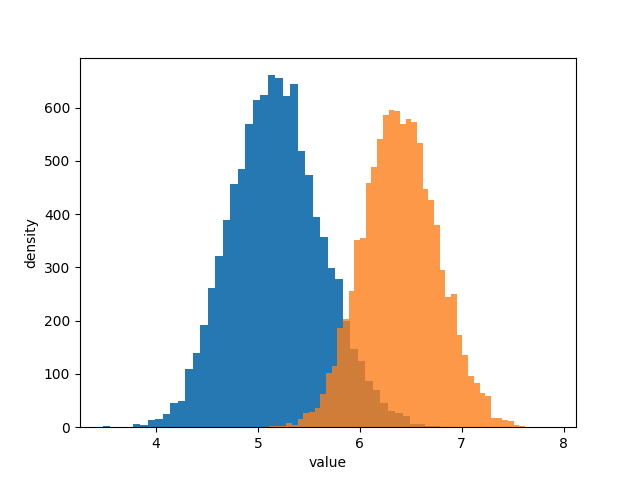
2. 从后验分布概率图中我们得到了什么初步的推断信息

从上图中我们可以得到如下信息：

. 两个后验的距离比较远，说明两种页面的表现有很多差别，但这里只是一个感性的认知，具体差别多少不知道；
. 页面A的累计期望比页面B要少 $，看起来不多，但是每次浏览都有这样的差距，积少成多是很可观的，越是大型企业对这点感受越深；

3. 定量分析两种页面的后验差距

为了确认这种差距是真实存在的，我们来看看看看概率密度差距：

print(posterior_expected_revenue_B > posterior_expected_revenue_A).mean()

0.9804

结果为98%，这个值已经足够高了，业务方应该选择页面B的方案。

另一个有趣的视角是两种页面的后验差距，我们需要看看两种收入期望的后验在直方图中的间距：

# -*- coding: utf- -*-

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc as pm
from numpy.random import dirichlet
from IPython.core.pylabtools import figsize

N_A =
N_A_79 =
N_A_49 =
N_A_25 =
N_A_0 = N_A - (N_A_79 + N_A_49 + N_A_25)
observations_A = np.array([N_A_79, N_A_49, N_A_25, N_A_0])

N_B =
N_B_79 =
N_B_49 =
N_B_25 =
N_B_0 = N_B - (N_B_79 + N_B_49 + N_B_25)
observations_B = np.array([N_B_79, N_B_49, N_B_25, N_B_0])

prior_parameters = np.array([, , , ])

posterior_samples_A = dirichlet(prior_parameters+observations_A, size=)
posterior_samples_B = dirichlet(prior_parameters+observations_B, size=)

def expected_revenue(P):
    return  * P[:, ] +  * P[:, ] +  * P[:, ] +  * P[:, ]

posterior_expected_revenue_A = expected_revenue(posterior_samples_A)
posterior_expected_revenue_B = expected_revenue(posterior_samples_B)

posterior_diff = posterior_expected_revenue_B - posterior_expected_revenue_A

plt.hist(posterior_diff, histtype='stepfilled', color='#7A68A6', label='difference in revenue between B and A', bins=)
plt.vlines(, , , linestyles='--')
plt.xlabel('value')
plt.ylabel('density')
plt.show()

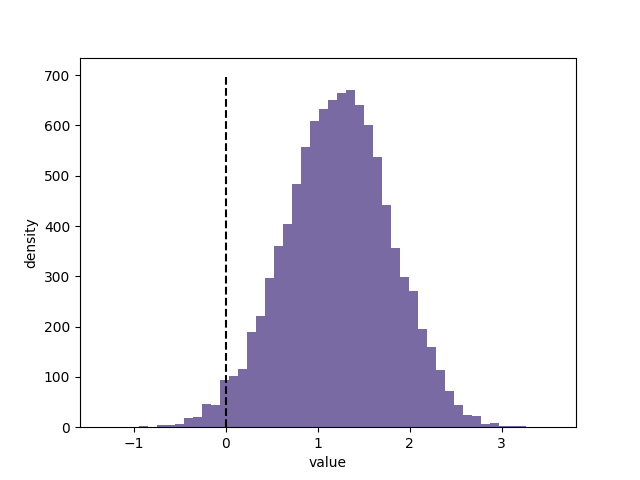
从上图中可以看到：

. 两者兼具有50%的概率大于 $，并且有一定可能大于 $；
. 即使我们选择B是错误的（虚线左边），也不会有太大的损失，分布上几乎不会超出 -0.5$ 太多；

0x6：A/B两组后验的增幅的估计

在进行了A/B测试后，决策者通常会对增幅感兴趣。但实际上，这里用增幅这个词是不准确的，贝叶斯估计的后验结果是一个分布，两个分布的增幅也是一个分布。

我们在学习贝叶斯统计的时候，一定要时刻注意将连续值问题和二值问题区分开来：

. 连续值问题是要衡量结果到底好多少，这是一定范围内的连续值（软分界）；
. 二值问题是要判断谁更好，只有两种可能（硬分界）；

1. 用后验分布的均值计算相对增幅合理吗？

一个很自然的想法是，用两个后验的均值计算相对增幅：

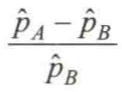
这会带来一些严重的错误。首先，这把对 Pa 和 Pb 的真实值的不确定性都掩盖起来了。在用均值差公式来计算增幅时，我们假定了这些值都是精确已知的（均值本质是一个统计压缩方法）。这几乎总是会高度这些值。

2. 计算后验分布的概率密度增幅

解决上述问题的方法就是，保留不确定性，统计学毕竟就是关于不确定性的理论。为此，我们可以直接将后验分布的概率密度函数相减，得到一个相减后的概率分布。

# -*- coding: utf- -*-

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc as pm
from scipy.stats import beta
from IPython.core.pylabtools import figsize

visitors_to_A =
visitors_to_B =
conversions_from_A =
conversions_from_B = 

alpha_prior =
beta_prior = 

posterior_A = beta(alpha_prior + conversions_from_A,
                   beta_prior + visitors_to_A - conversions_from_A)

posterior_B = beta(alpha_prior + conversions_from_B,
                   beta_prior + visitors_to_B - conversions_from_B)

samples =
samples_posterior_A = posterior_A.rvs(samples)
samples_posterior_B = posterior_B.rvs(samples)

print(samples_posterior_A > samples_posterior_B).mean()

def relative_increase(a, b):
    return (a - b) / b

posterior_rel_increase = relative_increase(samples_posterior_A, samples_posterior_B)

figsize(12.5, )

plt.hist(posterior_rel_increase, label='relative increase')
plt.xlabel('value')
plt.ylabel('density')
plt.show()

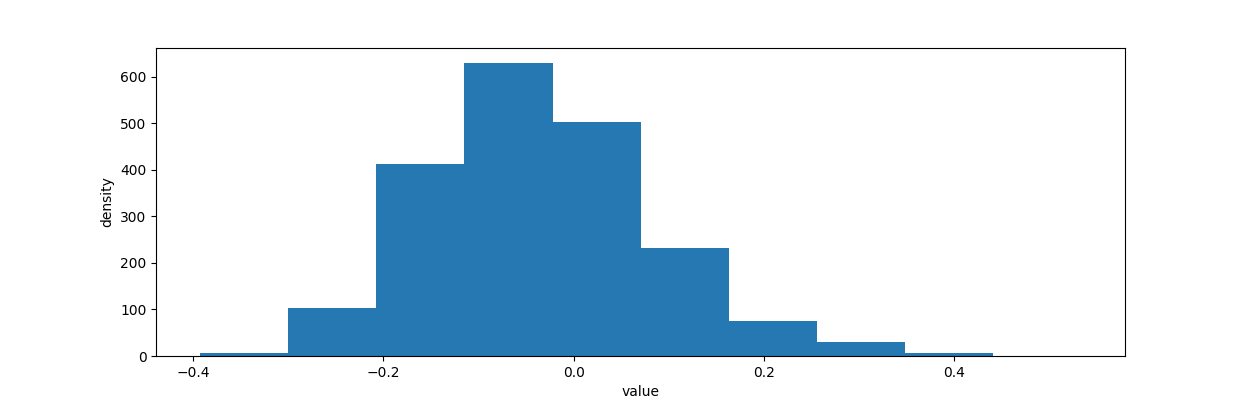
从上图中可以看出：

. 有89%的可能性，相对增幅会达到20%或者更多；
. 有72%的可能性，增幅能达到50%；

如果我们想要简单地使用均值点估计，即：

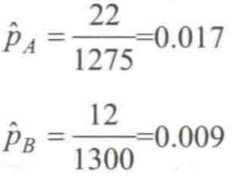
则关于增幅的均值点估计应该是87%，这显然太高了。

3. 创建后验概率增幅的点估计

我们继续增幅计算这个话题的讨论，尽管从贝叶斯统计角度来说，一切都是概率。但是直接把一个分布交给业务方是不合适的，业务方希望得到的结果就是一个精确的数值。那怎么办呢？解决的方法就是用统计压缩的方式，从分布中提取出一个”有代表性“的精确统计量来代替分布，有三种可选的方案：

. 返回增幅后验分布的均值：这个方法并不是非常好。原因在于对于一个倾斜的长尾分布，类似均值这样的统计量会很受影响，因而结论会过分表达长尾数据以至于高估实际的相对增幅；
. 返回增幅后验分布的中位数：中位数应该是更合理的值，它对于倾斜的分布会更有鲁棒性。然而在实践中，中位数仍然可能导致结论被高估；
. 返回增幅后验分布的百分位数（低于50%）。比如，返回第30%百分位数。这样做会有两个想要的特性：
　　）它相当于从数学上在增幅后验分布之上应用了一个损失函数。以惩罚过高的估计，这样估计的结果就更加保守
　　）随着我们得到越来越多的实验数据，增幅的后验分布会越来越窄，意味着任何百分位数都会收敛到同一个点

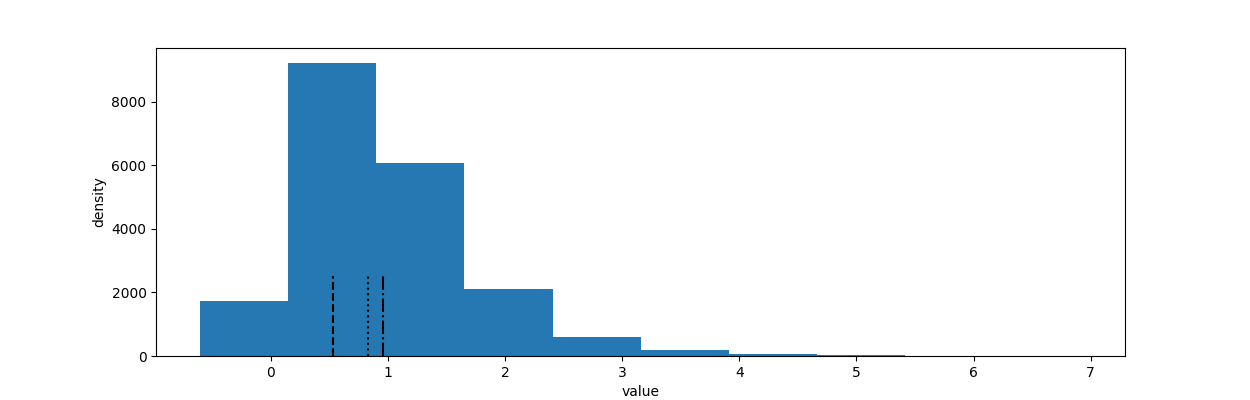
我们在下图中把三种统计量都画出来：

# -*- coding: utf- -*-

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import pymc as pm
from scipy.stats import beta
from IPython.core.pylabtools import figsize

visitors_to_A =
visitors_to_B =
conversions_from_A =
conversions_from_B = 

alpha_prior =
beta_prior = 

posterior_A = beta(alpha_prior + conversions_from_A,
                   beta_prior + visitors_to_A - conversions_from_A)

posterior_B = beta(alpha_prior + conversions_from_B,
                   beta_prior + visitors_to_B - conversions_from_B)

samples =
samples_posterior_A = posterior_A.rvs(samples)
samples_posterior_B = posterior_B.rvs(samples)

print(samples_posterior_A > samples_posterior_B).mean()

def relative_increase(a, b):
    return (a - b) / b

posterior_rel_increase = relative_increase(samples_posterior_A, samples_posterior_B)

mean = posterior_rel_increase.mean()
median = np.percentile(posterior_rel_increase, )
conservtive_percentile = np.percentile(posterior_rel_increase, )

figsize(, )

plt.hist(posterior_rel_increase, label='relative increase')
plt.vlines(mean, , , linestyles='-.', label='mean')
plt.vlines(median, , , linestyles=':', label='median')
plt.vlines(conservtive_percentile, , , linestyles='--', label='conservtive_percentile')
plt.xlabel('value')
plt.ylabel('density')
plt.show()