北航OO第一单元总结

我本着公平公开公正的态度作出以下评价：

1、面向对象真的很修身养性

2、有一个好的身体非常重要

3、互相hack可以暴露人的阴暗面

好了，步入正题。

一、作业分析

1、第一次作业分析

1.1类图

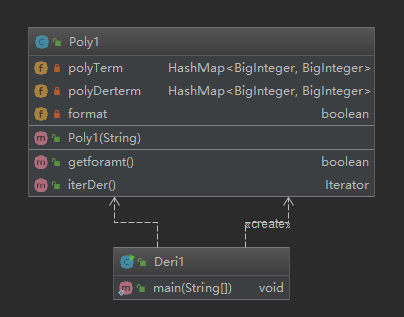
1.1.2基于度量的分析

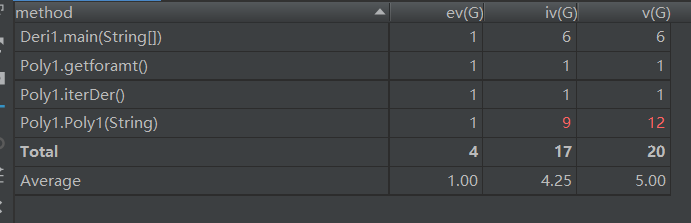
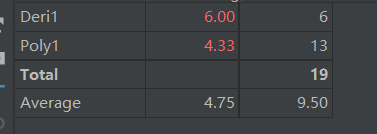
由于只有两个类，而Deri()类几乎什么都没做的，导致Poly类的复杂度较高。一开始写OO当成面向过程来写，结果把大部分功能都放在构造函数里面一起实现了。

1.2心路历程思考过程

当时对于面向对象没什么概念，照着面向过程就去写代码了。第一次作业是简单的多项式，两个类解决问题，一个用来存储，一个用来求导。（事实上，在写代码的时候，求导过程和存储放在了一起，而Derivation类形同虚设，只是一个main（）函数）。由于第一次的输入比较简单，和大部分人一样，我选择了大正则匹配，将匹配到的单项式存入Polynomial，并完成求导，再将求导结果返回给Derivativation。而格式判断的工作则是在正则匹配时不停地删去已匹配的项，若字符串最后为空，即格式正确。

1.3制造bug的原因

一个主要bug是空白符的问题，指导书中只要求space和\t,而我用\s实现的空格匹配。

2、第二次作业分析

2.1类图

2.1.2基于度量的分析

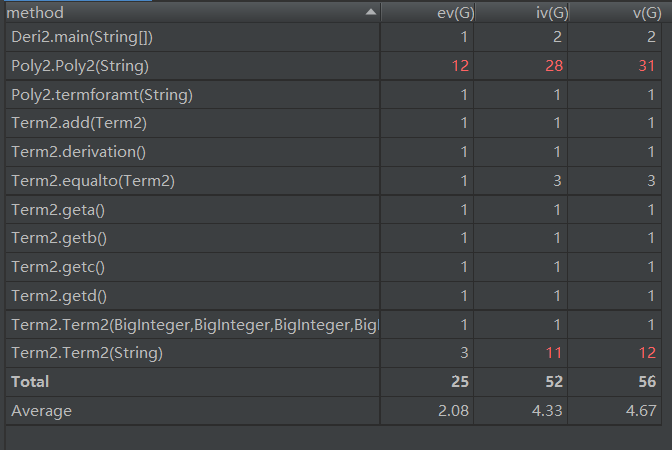
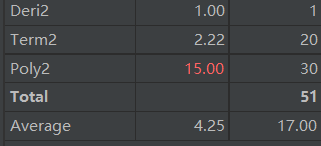
可以看出，实例化一个对象的复杂度较高，尤其是Poly类。这次作业和第一次作业一样，把大部分功能都放在了构造函数当中。

2.2思考过程

第二次作业引入了三角函数sin(x)和cos(x)，相较于第一次的正则，这一次更加复杂，但是我们依然可以选择头铁的用大正则解决（会面临爆栈问题），这样就连格式判断的问题也一并解决了。在匹配到单项式之后，先进行通过replace操作将所有单项式符号归一化以方便后续处理（例如：删空格，删加号，减号合并），再对单项式进行逐个读入，存储系数和三个指数。并且增加了equal()方法和add()方法用来合并同类项。求导操作也是在Term类里完成的。最后的简化输出则由Poly类实现，但是在实现过程要不断向Term索要指数，系数，不得不增加geta(),getb(),getc(),getd()四个方法，这属于设计上的纰漏。

2.3制造bug的原因

在Term初步归一化时，前置负号没有处理（其实处理了，半夜误删了那一段代码）。

没有仔细看指导书，在Poly类里少了两种空格插入的情况。

3、第三次作业分析

3.1类图

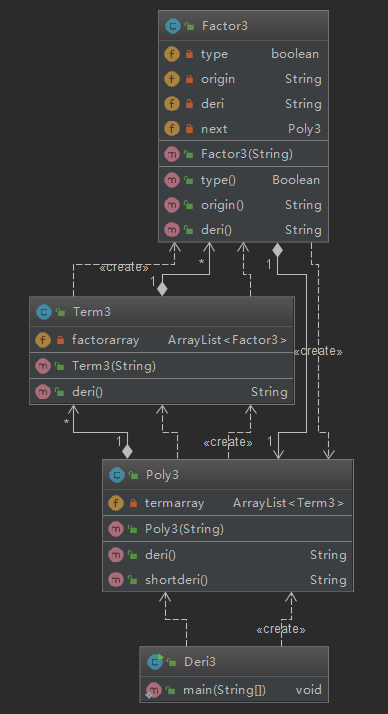
3.1.2基于度量的分析

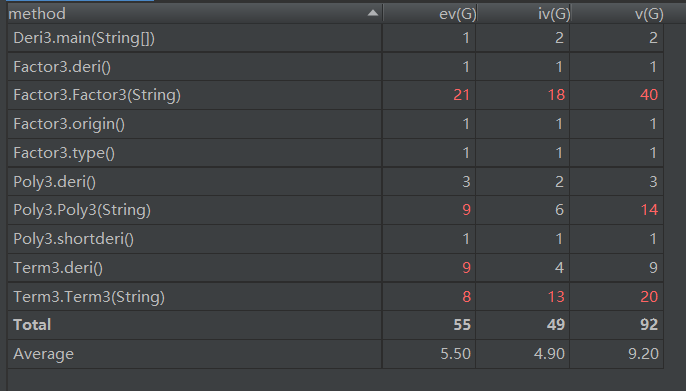
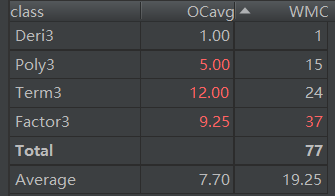
我对比了一下别人的代码复杂度，我第三次作业的复杂度算是炸了，可能是类太少，干得活太多.....除了Deri()类，其他类都挺辛苦的，我都不好意思分析了.....反正能者多劳吧，三个类都挺复杂的。好在这次不仅是构造函数比较辛苦，求导也复杂度比较高，一家人就应该整整齐齐。

2.2思考过程

第三次作业是最复杂的一次，也是我做得最简单的一次。大部分时间都花在了构思上，所以敲起代码反而得心应手。大正则的时代已经过去了，这次我选做了通过正负号来切分多项式，再通过乘号来切分因子。问题的难点在于括号的干扰，当然这对于大佬不是问题。我用了一个比较笨的办法，匹配到括号开始另一段正则匹配，数到相同数量的左右括号时再开始之前的加（乘）号匹配。对因子分情况求导，当因子是基础因子时（不含多项式）返回特定结果，因子不是特定因子时，对组成因子的多项式进行递归存储。这样存储以后，求导的时候就很简单，我们只需要把他的下一级看成一个整体，就可以很容易地表示出这一级的导函数，直到基础因子时，返回基础因子的导数。在返回导函数的同时，我还对系数，指数为0，和为1的情况在每一级进行化简，以减少递归时的计算压力。这样做的时候，输入格式判断也变简单了。只要上一级的输入，不满足这一层的接口，则抛出异常。可以看出，在整个计算过程中，我完全抛弃了int型（或BigInteger型）的变量，全部都是以String的形式进行传递，这样做简单粗暴，但是不利于最后的化简。不过对于我这样咸鱼玩家来说，也没有化简的必要了。

2.3制造bug的原因

对于输出结果，专门写了一个shortderi()方法，其中存在错误的化简。

没有仔细看指导书，无视了大整数，在factor类中错误地抛出异常。

4、总览

仔细看指导书会减少bug，减少因为“无知”产生的bug。

花时间放在构思上，比花时间放在修补上更值得。

二、分析bug的策略及问题

策略：

1、在自己写程序时，每注意到一个点，就写一个测试数据，到最后会有一个小规模的测试集，虽然这个测试集对于自己的程序没什么杀伤力，但对于别人的程序，可能是个不错的武器。

2、系统地构造wrong fromat的情况，尽可能排列出所有元素小于4个的组合

3、构造复杂的输入

4、脚本生成规范的输入，将输出结果与matlab自动比对

测bug的不足：

1、没有覆盖全面的format

2、没有覆盖全面的计算结果

PS：没有结合除自己以外被测者的代码设计结构构造样例。