洛谷P1140 基因匹配 //DP真正意义上的一血

题目背景

大家都知道，基因可以看作一个碱基对序列。它包含了44种核苷酸，简记作A,C,G,TA,C,G,T。生物学家正致力于寻找人类基因的功能，以利用于诊断疾病和发明药物。

在一个人类基因工作组的任务中，生物学家研究的是：两个基因的相似程度。因为这个研究对疾病的治疗有着非同寻常的作用。

题目描述

两个基因的相似度的计算方法如下：

对于两个已知基因，例如AGTGATGAGTGATG和GTTAGGTTAG，将它们的碱基互相对应。当然，中间可以加入一些空碱基-，例如：

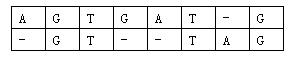
这样,两个基因之间的相似度就可以用碱基之间相似度的总和来描述，碱基之间的相似度如下表所示：

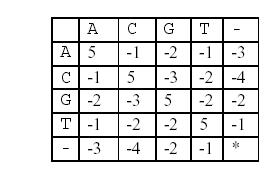
那么相似度就是：(-3)+5+5+(-2)+(-3)+5+(-3)+5=9(−3)+5+5+(−2)+(−3)+5+(−3)+5=9。因为两个基因的对应方法不唯一，例如又有：

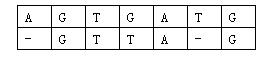
相似度为：(-3)+5+5+(-2)+5+(-1)+5=14(−3)+5+5+(−2)+5+(−1)+5=14。规定两个基因的相似度为所有对应方法中，相似度最大的那个。

输入输出格式

输入格式：

共两行。每行首先是一个整数，表示基因的长度；隔一个空格后是一个基因序列，序列中只含A,C,G,TA,C,G,T四个字母。1 \le1≤序列的长度\le 100≤100。

输出格式：

仅一行，即输入基因的相似度。

输入输出样例

输入样例#1：

7 AGTGATG
5 GTTAG

输出样例#1：

14

---

---

其实本蒟蒻以前做过DP题 但是这是第一次自己构造DP方程并且AC

对于我来说这个题的难点在于判断是谁插谁= =（听着好奇怪

对于每一个f[i][j]

1. 可以由f[i][j-1]转移而来
2. 可以由f[i-1][j]转移而来
3. 可以由f[i-1][j-1]转移而来

现在来讨论每一种情况

• f[i][j-1]转移

　　新来的b[j]要与一个空碱基匹配

　　相当于在A串上插了一个空碱基 并与B[j]进行匹配 f[i][j] = f[i][j-1] + trs[b[j][0];

• f[i-1][j]转移

　　新来的a[i]要与一个空碱基匹配

　　f[i][j] = f[i-1][j] + trs[a[i]][0];

• f[i-1][j-1]转移

　　相互匹配 f[i][j] =f[i-1] [j-1] + trs[a[i]][b[j]];

所以构造完成 循环顺序普通即可（想思考也可以想一下）

那么边界？可以想到f[i][0] =f[i-1][0] + trs[a[i]][0];

b也同理

分析完啦 上代码：

#include<bits/stdc++.h>
using namespace std;
int f[][];
int a[],b[],len2,len1;
int main(){
    const int trs[][]=
    {
         {,-,-,-,-},
         {-,,-,-,-},
         {-,-,,-,-},
         {-,-,-,,-},
         {-,-,-,-,}
     };
    cin>>len1;
    for(int i=;i<=len1;i++){
        char tra1;
        cin>>tra1;
        if(tra1=='A') a[i] = ;
        if(tra1=='C') a[i] = ;
        if(tra1=='G') a[i] = ;
        if(tra1=='T') a[i] = ;
    }
    cin>>len2;
    for(int i=;i<=len2;i++){
        char tra1;
        cin>>tra1;
        if(tra1=='A') b[i] = ;
        if(tra1=='C') b[i] = ;
        if(tra1=='G') b[i] = ;
        if(tra1=='T') b[i] = ;
    }
    for(int i=;i<=len1;i++){
        for(int j=;j<=len2;j++){
            f[i][j] = -0x3f3f3f3f;
        }
    }
    f[][] = ;
    for(int i=;i<=len1;i++){
        f[i][] = f[i-][] + trs[a[i]][];
    }
    for(int i=;i<=len2;i++){
        f[][i] = f[][i-] + trs[][b[i]];
    }

    for(int i=;i<=len1;i++){
        for(int j=;j<=len2;j++){
            f[i][j] = max(f[i-][j-] + trs[a[i]][b[j]] ,f[i][j]);
            f[i][j] = max(f[i-][j] + trs [a[i]] [], f[i][j]);//这里刚开始一直没有想清楚呜呜呜呜呜
            f[i][j] = max(f[i][j-] + trs [] [b[j]], f[i][j]);
        }
    }
    cout<<f[len1][len2]<<endl;
    return ;
}

真的是好不容易啊 呜呜呜呜呜我好弱2节课做了个这SB题；

但是感觉DP思维提升一些 也算没亏吧

---

TAG : SIN_XIII ⑨