Codeforces 1413F - Roads and Ramen（树的直径+找性质）

Codeforces 题目传送门 & 洛谷题目传送门

其实是一道还算一般的题罢……大概是最近刷长链剖分，被某道长链剖分与直径结合的题爆踩之后就点开了这题。

本题的难点就在于看出一个性质：最长路径的其中一个端点一定是直径的某一个端点。

证明：首先我们找出原树的一个直径，如果直径上标记边的个数为偶数那显然这条直径就是最优解，符合题意，否则我们假设我们找出的直径为 \(AB\)，我们已经找出了一条符合要求的路径 \(CD\)，下证我们总可以通过调整 \(CD\) 的端点，找出一条以 \(A\) 或 \(B\) 为端点的符合要求的路径，并且长度不劣于路径 \(CD\)。

分两种情况讨论：

• 若 \(CD\) 与 \(AB\) 没有公共边，那么我们总可以找到一个点 \(E\) 属于路径 \(CD\)，并且 \(E\) 到直径 \(AB\) 的最短路径上不包含属于路径 \(CD\) 的边，假设直径 \(AB\) 上到 \(E\) 距离最短的点为 \(F\)，由 \(CD\) 为符合要求的路径可知 \(CE,DE\) 两条路径上标记边的奇偶性相同，而由 \(AB\) 不符合题意可知 \(AF,BF\) 路径上标记边奇偶性不同，从而 \(AE,BE\) 奇偶性也不同，根据抽屉原理，在 \(AE,BE\) 中总有一者奇偶性与 \(CE\) 相同，不妨设为 \(AF\)，那么考虑路径 \(AC\)，由于 \(AE,CE\) 奇偶性相同，故路径 \(AC\) 符合条件，而由 \(AB\) 为直径可知 \(AE\ge DE\)，否则 \(BD\) 长度就超过 \(AB\) 了，因此我们得到了长度不劣于 \(CD\) 的路径 \(AB\)。

  

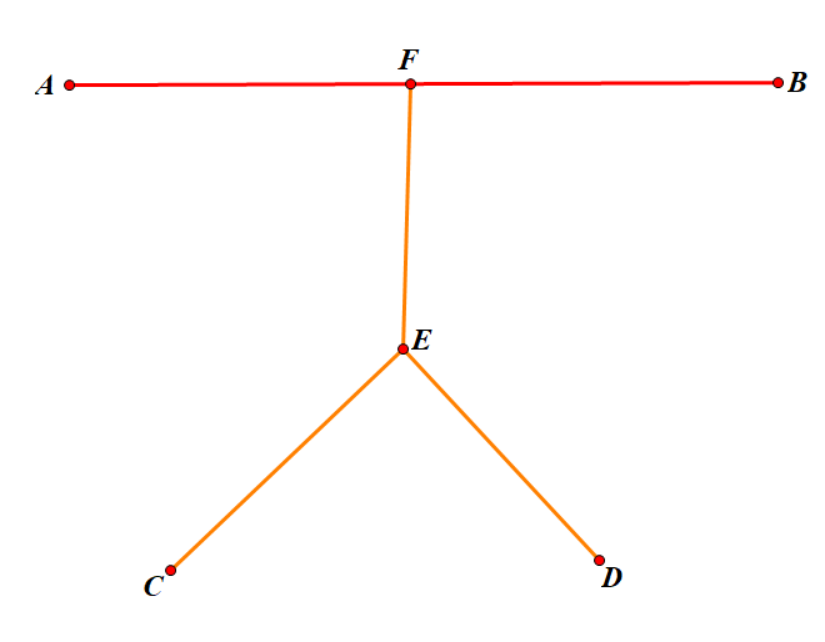
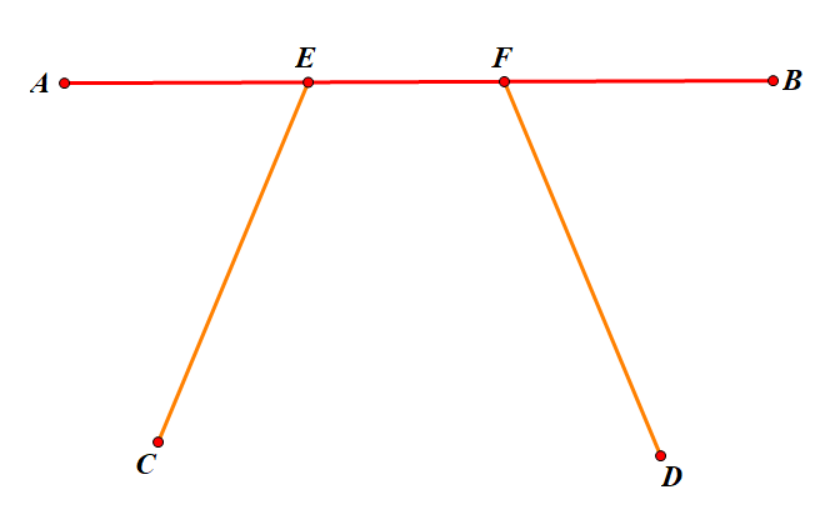
• 若 \(CD,AB\) 有公共部分，不妨设公共部分为 \(EF\)，根据路径 \(EF\) 上标记边的奇偶性又可分为两类，若 \(EF\) 上有奇数条标记边，由 \(AB\) 不合法可知 \(AE,BF\) 上标记边奇偶性相同，\(CD\) 合法可知 \(CE,DF\) 上标记边奇偶性不同，故 \(CE,DF\) 中总有一者奇偶性与 \(AE\) 相同，若为 \(DF\)，则 \(AF\) 满足条件，否则 \(CE\) 与 \(AE\) 奇偶性相同，\(AE\) 由与 \(BF\) 奇偶性相同，故 \(BF,CE\) 奇偶性相同，故 \(BE\) 满足条件，而根据直径的性质可知 \(AF,BE\) 的长度都不小于 \(CD\) 的长度，符合题意。若 \(EF\) 上有偶数条标记边，仿照之前的推理过程可知 \(AF,BE\) 中恰好存在一个符合要求的路径，得证。

  

接下来考虑知道这个性质之后怎样解题，我们先两边 DFS 在线性时间内求出树的直径，然后以两个直径分别为根再跑一遍 DFS 求出 DFS 序（这样方便后面修改，可用 DFS 序将子树操作转化为区间操作）并分别建一棵线段树，线段树上每个区间 \([l,r]\) 维护两个值 \(mx0,mx1\)，分别表示 DFS 序在 \([l,r]\) 中并且到当前根节点路径上有偶数条标记边的点中，深度的最大值；以及DFS 序在 \([l,r]\) 中并且到当前根节点路径上有奇数条标记边的点中，深度的最大值，修改则相当于对子树打标记，这个可用区间懒标记实现，下推标记时交换节点的 \(mx0,mx1\) 即可，查询则直接返回全局最大值，两种情况取个 \(\max\) 即可。时间复杂度 \(\mathcal O(n\log n)\)。

这道题告诉我们，碰到那种求满足什么条件的长度最大的路径时，常可以往树的直径方面想。

#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
typedef unsigned int u32;
typedef unsigned long long u64;
namespace fastio{
	#define FILE_SIZE 1<<23
	char rbuf[FILE_SIZE],*p1=rbuf,*p2=rbuf,wbuf[FILE_SIZE],*p3=wbuf;
	inline char getc(){return p1==p2&&(p2=(p1=rbuf)+fread(rbuf,1,FILE_SIZE,stdin),p1==p2)?-1:*p1++;}
	inline void putc(char x){(*p3++=x);}
	template<typename T> void read(T &x){
		x=0;char c=getchar();T neg=0;
		while(!isdigit(c)) neg|=!(c^'-'),c=getchar();
		while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
		if(neg) x=(~x)+1;
	}
	template<typename T> void recursive_print(T x){if(!x) return;recursive_print(x/10);putc(x%10^48);}
	template<typename T> void print(T x){if(!x) putc('0');if(x<0) putc('-'),x=~x+1;recursive_print(x);}
	void print_final(){fwrite(wbuf,1,p3-wbuf,stdout);}
}
const int MAXN=5e5;
int n,qu,hd[MAXN+5],to[MAXN*2+5],val[MAXN*2+5],nxt[MAXN*2+5],ec=0;
void adde(int u,int v,int w){to[++ec]=v;val[ec]=w;nxt[ec]=hd[u];hd[u]=ec;}
namespace getdia{
	int dep1[MAXN+5],dep2[MAXN+5],rt1=1,rt2=1;
	void dfs1(int x,int f){
		for(int e=hd[x];e;e=nxt[e]){
			int y=to[e];if(y==f) continue;
			dep1[y]=dep1[x]+1;dfs1(y,x);
		}
	}
	void dfs2(int x,int f){
		for(int e=hd[x];e;e=nxt[e]){
			int y=to[e];if(y==f) continue;
			dep2[y]=dep2[x]+1;dfs2(y,x);
		}
	}
	void finddia(){
		dfs1(1,0);for(int i=1;i<=n;i++) if(dep1[i]>dep1[rt1]) rt1=i;
		dfs2(rt1,0);for(int i=1;i<=n;i++) if(dep2[i]>dep2[rt2]) rt2=i;
	}
}
struct solver{
	int rt,dfn[MAXN+5],edt[MAXN+5],tim=0,rid[MAXN+5];
	int par[MAXN+5],dw[MAXN+5],dep[MAXN+5];
	void dfs(int x,int f){
		dfn[x]=++tim;rid[tim]=x;
		for(int e=hd[x];e;e=nxt[e]){
			int y=to[e],z=val[e];if(y==f) continue;
			dw[e+1>>1]=y;par[y]=par[x]^z;dep[y]=dep[x]+1;dfs(y,x);
		} edt[x]=tim;
	}
	struct node{int l,r,mx[2],flp;} s[MAXN*4+5];
	void pushup(int k){
		s[k].mx[0]=max(s[k<<1].mx[0],s[k<<1|1].mx[0]);
		s[k].mx[1]=max(s[k<<1].mx[1],s[k<<1|1].mx[1]);
	}
	void build(int k,int l,int r){
		s[k].l=l;s[k].r=r;if(l==r){s[k].mx[par[rid[l]]]=dep[rid[l]];return;}
		int mid=l+r>>1;build(k<<1,l,mid);build(k<<1|1,mid+1,r);pushup(k);
	}
	void pushdown(int k){
		if(s[k].flp){
			swap(s[k<<1].mx[0],s[k<<1].mx[1]);s[k<<1].flp^=1;
			swap(s[k<<1|1].mx[0],s[k<<1|1].mx[1]);s[k<<1|1].flp^=1;
			s[k].flp=0;
		}
	}
	void modify(int k,int l,int r){
		if(l<=s[k].l&&s[k].r<=r){
			s[k].flp^=1;swap(s[k].mx[0],s[k].mx[1]);return;
		} pushdown(k);int mid=s[k].l+s[k].r>>1;
		if(r<=mid) modify(k<<1,l,r);
		else if(l>mid) modify(k<<1|1,l,r);
		else modify(k<<1,l,mid),modify(k<<1|1,mid+1,r);
		pushup(k);
	}
	int query(){return s[1].mx[0];}
	void init(){dfs(rt,0);build(1,1,n);}
	void toggle(int x){modify(1,dfn[dw[x]],edt[dw[x]]);}
} t[2];
int main(){
	scanf("%d",&n);
	for(int i=1,u,v,w;i<n;i++) scanf("%d%d%d",&u,&v,&w),adde(u,v,w),adde(v,u,w);
	getdia::finddia();t[0].rt=getdia::rt1;t[1].rt=getdia::rt2;t[0].init();t[1].init();
	int qu;scanf("%d",&qu);
	while(qu--){
		int x;scanf("%d",&x);t[0].toggle(x);t[1].toggle(x);
		printf("%d\n",max(t[0].query(),t[1].query()));
	}
	return 0;
}