ACwing02.01背包问题

有\(N\)件物品和一个容量是\(V\)的背包。每件物品只能使用一次。

第\(i\)件物品的体积是\(v_i\)，价值是\(w_i\)。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行两个整数，\(N\)，\(V\)，用空格隔开，分别表示物品数量和背包容积。

接下来有 \(N\) 行，每行两个整数 \(v_i\),\(w_i\)，用空格隔开，分别表示第 \(i\) 件物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

\(0<N,V≤1000\)

\(0<v_i,w_i≤1000\)

输入样例

4 5

1 2

2 4

3 4

4 5

输出样例：

8

---

思路：



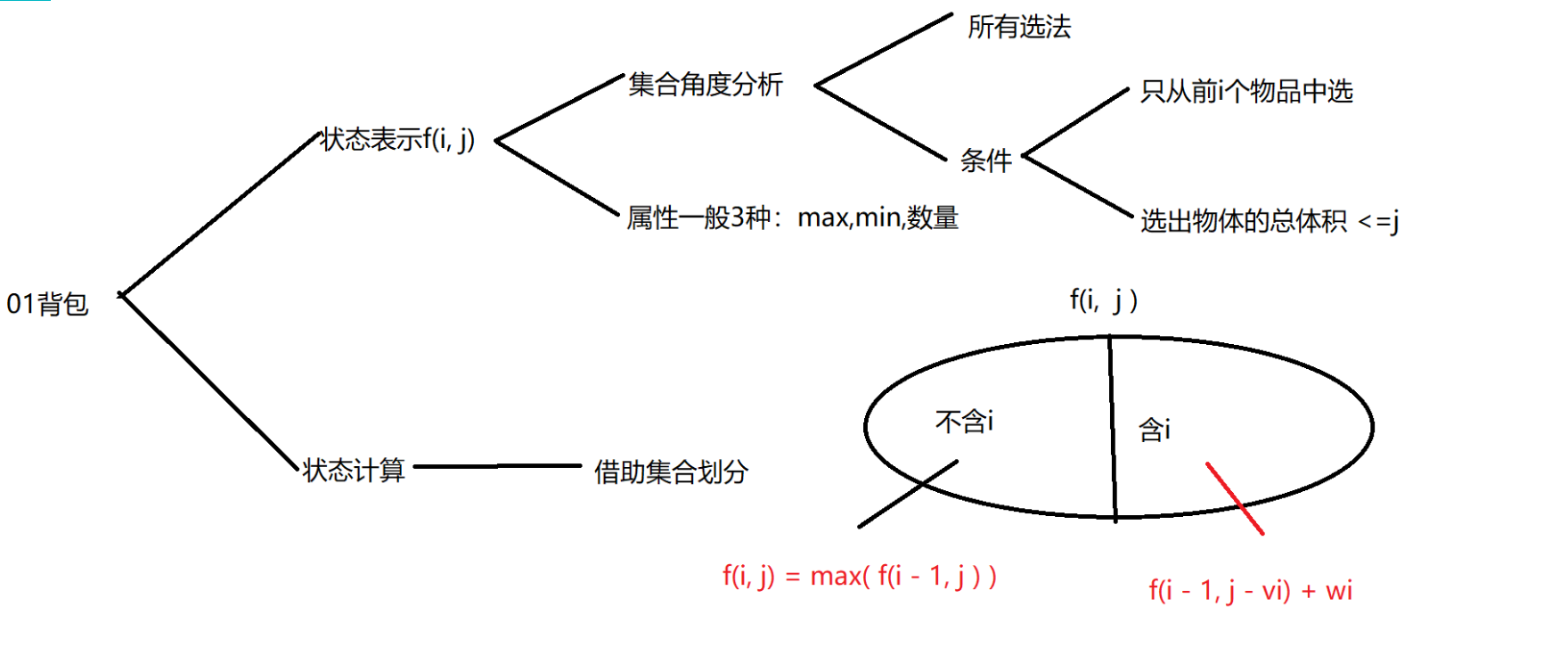
借助闫式DP分析法、把这个问题从集合的角度来分析，将问题分成状态表示和状态计算。

状态表示：

本题的状态可以用f(i, j)来表示、这表示的是从前\(i\)个物品中选、选出物体的总体积小于等于\(j\)的物品。

状态计算：

那么、借助\(f(i, j)\)、可以在集合的角度将问题一分为二来看、即所有不含\(i\)的物品和含\(i\)的物品。

不含\(i\)：即、从1、2···i-1、中选、选出物体的总价值不大于\(j\)的物品、故容易表示为\(f(i,j) = f(i - 1, j)\)。

含\(i\)的物品：这里我们不好直接求到这个状态、可以先减去所有不含\(i\)的、再将权重加回去、此时可以得到状态\(f(i - 1, j - v_i) + w_i\)。(不一定存在、\(j >= v_i\) 时存在)

---

代码：

#include <iostream>

using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N][N];    // 状态数组

int main()
{
    int n, m;

    cin >> n >> m;

    for(int i = 1 ; i <= n ; i ++ ) cin >> v[i] >> w[i];

    // 从第一件物品开始选、价值可以为0
    for(int i = 1 ; i <= n ; i ++ )
        for(int j = 0 ; j <= m ; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if(j >= v[i])
            {
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
            }
        }

    // 从前n个物品中选、总价值不超过m即为所求
    cout << f[n][m] << endl;

    return 0;
}