[PGM] Exact Inference for calculating marginal distribution

如何在贝叶斯网络中求解某变量的边缘分布？

这是一个问题。

---

贝叶斯网络如下：

CPTs如下：

(1) How to compute p( L | C = high )？

---

p( L | C = high )

= p(L, C=high) / p(C=high) 　　// Bayesian Theorem.

= Joint dist / p(C=high)　　// 但是这里需要的却是joint dist!

求 Joint dist，便想到 变量消减，如下：

p( L, C)

= Σ ... Σ p(H) * p(L) * p(A) * p(V|H,L) * p(S|H,L) * p(C|V) * p(O|V,S) * p(B|O,T) * p(T|A)　　// 积分掉与L,C没任何关系的部分，加和=1

= Σ_H Σ_V p(H) * p(L) * p(V|H,L) * p(C|V) 　　// 可见，结果只保留了与L,C有关的部分；因为H,V与L,C有牵扯，所以没法加和消减掉变量

= p(L) Σ_V p(C|V) Σ_H p(H) * p(V|H,L)

注意：消元的顺序不能胡来：

比如p(O|V,S)是可以最终消掉的，但O还作为了p(B|O,T)的条件部分，所以，

• 先消掉p(B|O,T)  (如果B此时能消，也即是不在其他地方充当条件)
• 然后才能消O。

之后就是穷举V, H的过程。

先处理这一个部分：

Σ_H p(H) * p(V|H,L) 　　// 可见，除了H，剩余的两个变量(V,L)需要穷举所有离散情况，以便消减掉H

1. Σ_H p(H) * p(V=low |H,L=true )

2. Σ_H p(H) * p(V=high|H,L=true ) = 1 - Σ_H p(H) * p(V=low|H,L=true ) 　　// 求出1，即自动得出2

3. Σ_H p(H) * p(V=low |H,L=false)

4. Σ_H p(H) * p(V=high|H,L=false) = 1 - Σ_H p(H) * p(V=low|H,L=false) 　　// 求出3，即自动得出4

计算过程：

1. Σ_H p(H) * p(V=low |H,L=true ) 等价于 p(V=low |L=true )

= p(H=true) * p(V=low|H=true,L=true) + p(H=false) * p(V=low |H=false,L=true) 　　// 变为了可查表的形式

= 0.2 * 0.95 + 0.8 * 0.01

= 0.198

2. Σ_H p(H) * p(V=high|H,L=true ) 等价于 p(V=high|L=true )

= 1 - Σ_H p(H) * p(V=low|H,L=true )

= 1 - 0.198

= 0.802

3. Σ_H p(H) * p(V=low |H,L=false) 等价于 p(V=low |L=false)

= p(H=true) * p(V=low|H=true,L=false) + p(H=false) * p(V=low |H=false,L=false) 　　// 变为了可查表的形式

= 0.2 * 0.98 + 0.8 * 0.05

= 0.236

4. Σ_H p(H) * p(V=high|H,L=false) 等价于 p(V=high|L=false)

= 1 - Σ_H p(H) * p(V=low|H,L=false)

= 1 - 0.236

= 0.764

再处理剩下的部分：

p(L) * Σ_v p(C|V) * p(V|L) 　　// 可见，除了V，剩余的两个变量(C,L)需要穷举所有离散情况，以便消减掉V

1. p(L=true ) * Σ_v p(C=high|V) * p(V|L=true ) 

2. p(L=false) * Σ_v p(C=high|V) * p(V|L=false)　　// 注意，Σ_v外有p(L)，故不能直接采用补集的方法计算

计算过程：

1. p(L=true ) * Σ_v p(C=high|V) * p(V|L=true ) 等价于 p(L=true, C=high)

= p(L=true ) * p(C=high|V=low ) * p(V=low |L=true) + p(L=true ) * p(C=high|V=high) * p(V=high|L=true ) 

= 0.05 * 0.01 * 0.198 + 0.05 * 0.7 * 0.802

= 0.028169

2. p(L=false) * Σ_v p(C=high|V) * p(V|L=false) 等价于 p(L=false, C=high)

= p(L=false) * p(C=high|V=low ) * p(V=low |L=false) + p(L=false) * p(C=high|V=high) * p(V=high|L=false) 

= 0.95 * 0.01 * 0.236 + 0.95 * 0.7 * 0.764

= 0.510302

Result:

p( L | C = high )

= p(L, C=high) / { p(C=high) }　　// Bayesian Theorem.

= p(L, C=high) / { p(L=true, C=high) + p(L=false, C=high) }

= p(L, C=high) / { 0.028169 + 0.510302 }

可见，结果就是Bernoulli distribution with probability with theta = 0.028169/(0.028169 + 0.510302)=0.052312938

(2) Then, compute p( L | C = high ) using the Junction Tree Algorithm. 

---

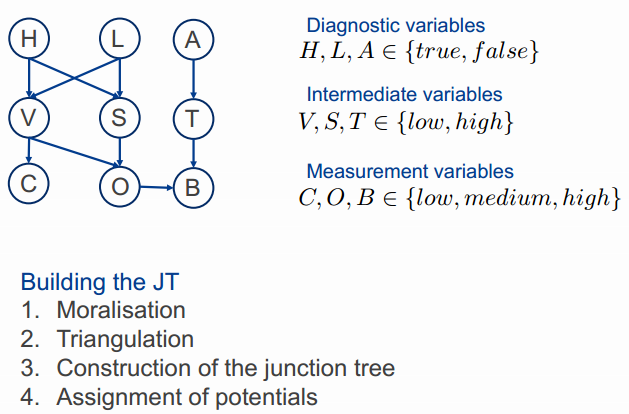
1. Moralisation

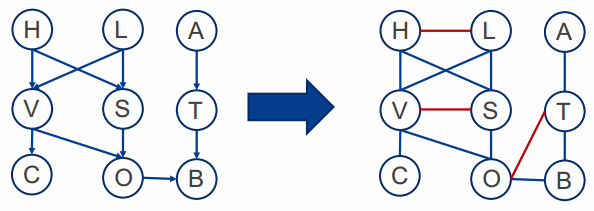
2. Triangulation

得到clique：{A, T}, {O,T,B}, {V, S,O}, {V, C}, {V, H, L, S}

3. Construction of the junction tree

4. Assignment of potentials

ψ(CV)   = P(C|V)
ψ(VSO)  = P(O|V,S)
ψ(VHLS) = P(V|H,L)P(S|H,L)P(H)P(L)
ψ(OTB)  = P(B|O,T)
ψ(TA)   = P(T|A)P(A)
Φ(V) = Φ(VS) = Φ(O) = Φ(T) = 1

根据以下算法更新evidence：

　　

　　From left to right: 

Φ(V) = 1

Φ*(V) = Σ_c ψ(CV) = Σ_c P(C|V) = P(C = high|V)

From right to left: 

Φ(T) = 1

Φ*(T) = Σ_a ψ(TA) = Σ_a P(T|A)P(A) = P*(T)

ψ(OTB) = P(B|O,T)

ψ*(OTB) = ψ(OTB) x Φ*(T)/Φ(T) = ψ(OTB)

Φ(O) = 1

Φ*(O) = Σ_tb ψ(OTB) = Σ_tb P(B|O,T) = 1

ψ(VSO) = P(O|V,S)

ψ*(VSO) = ψ(VSO) x Φ*(O)/Φ(O) = ψ(VSO)

Φ(VS) = 1

Φ*(VS) = Σ_o ψ(VSO) = Σ_o P(O|V,S) = 1

更新 { V H L S }：

ψ*(VHLS)

= ψ(VHLS) x { Φ*(V) x Φ*(VS) } / { Φ(V) x Φ(VS) }

= P(V|H,L) * P(S|H,L) * P(H) * P(L) * { P(C = high|V) * 1 } / { 1 * 1 }

= P(V|H,L) * P(S|H,L) * P(H) * P(L) * P(C = high|V) 

注意：我们当下已获得了置信传播的一个结果，就是 ψ*(VHLS)，消息从左右两边都传递到了这里。

接下来，我们会如何用这个结果呢？这个结果又能给我们带来怎样的好处呢？

以下用于下一步的类比参考。

（1）用置信传播结果表示边缘条件概率

（2）头上加了小弯弯表示是已知变量，就是条件部分的变量。

照猫画虎就是如下：

p(L|C=high)

= p(L,C=high) / p(C=high)　　// Bayesian Theorem.

注意这里，分子分母的计算与传统方法比较时开始发生变化的地方，要体会。

已知：ψ*(VHLS)

分子：Σ_VHS ψ*(VHLS)

分母：Σ_VHSL ψ*(VHLS)

分母：（Ｌ这种情况下消不掉）

P(V|H,L) * P(S|H,L) * P(H) * P(L) * P(C = high|V) 

变为：Σ_VHL｛ P(V|H,L) * P(H) * P(L) * P(C = high|V) ｝

分子：

P(V|H,L) * P(S|H,L) * P(H) * P(L) * P(C = high|V) 

变为：Σ_VH｛ P(V|H,L) * P(H) * P(L) * P(C = high|V) ｝

可见，还是变为了穷举V，H的结果，最终也得到了方案（1）相同的结论。

后记：

这个例子可能不太完美，建议自己做一次P(O|H=true, L=true, A=true)。过程当中尤其体会对变量A的处理。

因为A是条件中的变量，所以在方法一中不能消去，这导致了计算资源的浪费；

在方法二中，就没有这个问题。好运。