Spark机器学习之协同过滤算法

Spark机器学习之协同过滤算法

　　　　一）、协同过滤

　　　　　　1.1 概念　　　　　　

　　　　　　　　　协同过滤是一种借助"集体计算"的途径。它利用大量已有的用户偏好来估计用户对其未接触过的物品的喜好程度。其内在思想是相似度的定义

　　　　　　　1.2 分类

　　　　　　　　　1.在基于用户的方法的中，如果两个用户表现出相似的偏好（即对相同物品的偏好大体相同），那就认为他们的兴趣类似。要对他们中的一个用户推荐一个未知物品，

　　　　　　　　便可选取若干与其类似的用户并根据他们的喜好计算出对各个物品的综合得分，再以得分来推荐物品。其整体的逻辑是，如果其他用户也偏好某些物品，那这些物品很可能值得推荐。

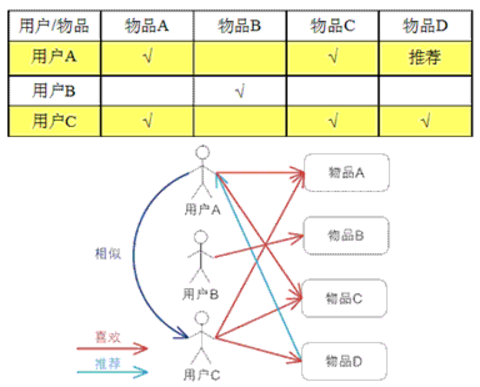
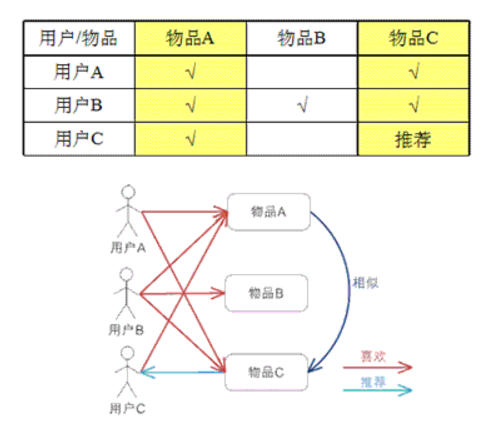
　　　　　　　　　　2. 同样也可以借助基于物品的方法来做推荐。这种方法通常根据现有用户对物品的偏好或是评级情况，来计算物品之间的某种相似度。

　　　　　　　　　　　　   这时，相似用户评级相同的那些物品会被认为更相近。一旦有了物品之间的相似度，便可用用户接触过的物品来表示这个用户，然后找出和这些已知物品相似的那些物品，

　　　　　　　　　　　　   并将这些物品推荐给用户。同样，与已有物品相似的物品被用来生成一个综合得分，而该得分用于评估未知物品的相似度。

　　　　二）、矩阵分解　　　　　　　　　　　　

　　　　　　Spark推荐模型库当前只包含基于矩阵分解（matrix factorization）的实现，由此我们也将重点关注这类模型。它们有吸引人的地方。首先，这些模型在协同过滤

　　　　　　中的表现十分出色。而在Netflix Prize等知名比赛中的表现也很拔尖

　　　　　　1，显式矩阵分解　　　　

　　　　　　　　　要找到和“用户物品”矩阵近似的k维（低阶）矩阵，最终要求出如下两个矩阵：一个用于表示用户的U × k维矩阵，以及一个表征物品的I × k维矩阵。

　　　　　　　　　这两个矩阵也称作因子矩阵。它们的乘积便是原始评级矩阵的一个近似。值得注意的是，原始评级矩阵通常很稀疏，但因子矩阵却是稠密的。

　　　　　　　　　特点：

　　　　　　　　　　因子分解类模型的好处在于，一旦建立了模型，对推荐的求解便相对容易。但也有弊端，即当用户和物品的数量很多时，其对应的物品或是用户的因子向量可能达到数以百万计。

　　　　　　　　　　这将在存储和计算能力上带来挑战。另一个好处是，这类模型的表现通常都很出色。

　　　　　　　2，隐式矩阵分解（关联因子分确定，可能随时会变化）

　　　　　　　　隐式模型仍然会创建一个用户因子矩阵和一个物品因子矩阵。但是，模型所求解的是偏好矩阵而非评级矩阵的近似。类似地，此时用户因子向量和物品因子向量的点积所得到的分数

　　　　　　　　也不再是一个对评级的估值，而是对某个用户对某一物品偏好的估值（该值的取值虽并不严格地处于0到1之间，但十分趋近于这个区间）

　　　　　　　3，最小二乘法（Alternating Least Squares    ALS）：解决矩阵分解的最优化方法

　　　　　　　　ALS的实现原理是迭代式求解一系列最小二乘回归问题。在每一次迭代时，固定用户因子矩阵或是物品因子矩阵中的一个，然后用固定的这个矩阵以及评级数据来更新另一个矩阵。

　　　　　　　　之后，被更新的矩阵被固定住，再更新另外一个矩阵。如此迭代，直到模型收敛（或是迭代了预设好的次数）。

　　　　三）、Spark下ALS算法的应用

　　　　　　　1，数据来源电影集ml-100k

　　　　　　　2,代码实现

　　　　　　　　基于用户相似度片段代码：　　　　　　　

val movieFile=sc.textFile(fileName)
    val RatingDatas=movieFile.map(_.split("\t").take(3))
    //转为Ratings数据
    val ratings=RatingDatas.map(x =>Rating(x(0).toInt,x(1).toInt,x(2).toDouble))
    //获取用户评价模型,设置k因子,和迭代次数,隐藏因子lambda,获取模型

    val model=ALS.train(ratings,50,10,0.01)
    //基于用户相似度推荐
    println("userNumber:"+model.userFeatures.count()+"\t"+"productNum:"+model.productFeatures.count())
    //指定用户及商品,输出预测值
    println(model.predict(789,123))
    //为指定用户推荐的前N商品
    model.recommendProducts(789,11).foreach(println(_))
    //为每个人推荐前十个商品
    model.recommendProductsForUsers(10).take(1).foreach{
      case(x,rating) =>println(rating(0))
    }

　　　　　　　基于商品相似度代码：

　　　　计算相似度的方法有相似度是通过某种方式比较表示两个物品的向量而得到的。常见的相似度衡量方法包括皮尔森相关系数（Pearson correlation）、针对实数向量的余弦相

似度（cosine similarity）和针对二元向量的杰卡德相似系数（Jaccard similarity）。

val itemFactory=model.productFeatures.lookup(567).head
    val itemVector=new DoubleMatrix(itemFactory)
    //求余弦相似度
    val sim=model.productFeatures.map{
      case(id,factory)=>
        val factorVector=new DoubleMatrix(factory)
        val sim=cosineSimilarity(factorVector,itemVector)
        (id,sim)
    }
    val sortedsim=sim.top(11)(Ordering.by[(Int,Double),Double]{
      case(id,sim)=>sim
    })
    println(sortedsim.take(10).mkString("\n"))
def cosineSimilarity(vec1:DoubleMatrix,vec2:DoubleMatrix):Double={
    vec1.dot(vec2)/(vec1.norm2()*vec2.norm2())
  }

　　　　　均方差评估模型代码：

//模型评估,通过均误差
    //实际用户评估值
    val actualRatings=ratings.map{
      case Rating(user,item,rats) => ((user,item),rats)
    }
    val userItems=ratings.map{
      case(Rating(user,item,rats)) => (user,item)
    }
    //模型的用户对商品的预测值
    val predictRatings=model.predict(userItems).map{
      case(Rating(user,item,rats)) =>((user,item),rats)
    }
    //联合获取rate值
    val rates=actualRatings.join(predictRatings).map{
      case x =>(x._2._1,x._2._2)
    }
    //求均方差
    val regressionMetrics=new RegressionMetrics(rates)
    //越接近0越佳
    println(regressionMetrics.meanSquaredError)

　　　　　　全局准确率评估（MAP）：使用MLlib的 RankingMetrics 类来计算基于排名的评估指标。类似地，需要向我们之前的平均准确率函数传入一个键值对类型的RDD。

　　　　　　其键为给定用户预测的推荐物品的ID数组，而值则是实际的物品ID数组。

//全局平均准确率(MAP)
    val itemFactors = model.productFeatures.map { case (id, factor)
    => factor }.collect()
    val itemMatrix = new DoubleMatrix(itemFactors)
    //分布式广播商品的特征矩阵
    val imBroadcast = sc.broadcast(itemMatrix)
    //计算每一个用户的推荐,在这个操作里，会对用户因子矩阵和电影因子矩阵做乘积，其结果为一个表示各个电影预计评级的向量（长度为
    //1682，即电影的总数目）
    val allRecs = model.userFeatures.map{ case (userId, array) =>
      val userVector = new DoubleMatrix(array)
      val scores = imBroadcast.value.mmul(userVector)
      val sortedWithId = scores.data.zipWithIndex.sortBy(-_._1)
      val recommendedIds = sortedWithId.map(_._2 + 1).toSeq   //+1,矩阵从0开始
      (userId, recommendedIds)
    }
    //实际评分
    val userMovies = ratings.map{ case Rating(user, product, rating) =>
      (user, product)}.groupBy(_._1)
    val predictedAndTrueForRanking = allRecs.join(userMovies).map{ case
      (userId, (predicted, actualWithIds)) =>
      val actual = actualWithIds.map(_._2)
      (predicted.toArray, actual.toArray)
    }
    //求MAP,越大越好吧
    val rankingMetrics = new RankingMetrics(predictedAndTrueForRanking)
    println("Mean Average Precision = " + rankingMetrics.meanAveragePrecision)

　　　　详细代码：

package com.spark.milb.study

import org.apache.log4j.{Level, Logger}
import org.apache.spark.mllib.evaluation.{RankingMetrics, RegressionMetrics}
import org.apache.spark.mllib.recommendation.{ALS, Rating}
import org.apache.spark.{SparkConf, SparkContext}
import org.jblas.DoubleMatrix

/**
  * Created by hadoop on 17-5-3.
  * 协同过滤(处理对象movie,使用算法ALS:最小二乘法(实现用户推荐)
  * 余弦相似度实现商品相似度推荐
  */
object cfTest {
  def main(args: Array[String]): Unit = {
    Logger.getLogger("org.apache.spark").setLevel(Level.WARN)
    Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)
    val conf=new SparkConf().setMaster("local").setAppName("AlsTest")
    val sc=new SparkContext(conf)
    CF(sc,"ml-100k/u.data")
  }
  def CF(sc:SparkContext,fileName:String): Unit ={
    val movieFile=sc.textFile(fileName)
    val RatingDatas=movieFile.map(_.split("\t").take(3))
    //转为Ratings数据
    val ratings=RatingDatas.map(x =>Rating(x(0).toInt,x(1).toInt,x(2).toDouble))
    //获取用户评价模型,设置k因子,和迭代次数,隐藏因子lambda,获取模型
    /*
    *   rank ：对应ALS模型中的因子个数，也就是在低阶近似矩阵中的隐含特征个数。因子个
          数一般越多越好。但它也会直接影响模型训练和保存时所需的内存开销，尤其是在用户
          和物品很多的时候。因此实践中该参数常作为训练效果与系统开销之间的调节参数。通
          常，其合理取值为10到200。
        iterations ：对应运行时的迭代次数。ALS能确保每次迭代都能降低评级矩阵的重建误
           差，但一般经少数次迭代后ALS模型便已能收敛为一个比较合理的好模型。这样，大部分
           情况下都没必要迭代太多次（10次左右一般就挺好）。
       lambda ：该参数控制模型的正则化过程，从而控制模型的过拟合情况。其值越高，正则
          化越严厉。该参数的赋值与实际数据的大小、特征和稀疏程度有关。和其他的机器学习
          模型一样，正则参数应该通过用非样本的测试数据进行交叉验证来调整。
    * */
    val model=ALS.train(ratings,50,10,0.01)
    //基于用户相似度推荐
    println("userNumber:"+model.userFeatures.count()+"\t"+"productNum:"+model.productFeatures.count())
    //指定用户及商品,输出预测值
    println(model.predict(789,123))
    //为指定用户推荐的前N商品
    model.recommendProducts(789,11).foreach(println(_))
    //为每个人推荐前十个商品
    model.recommendProductsForUsers(10).take(1).foreach{
      case(x,rating) =>println(rating(0))
    }
    //基于商品相似度(使用余弦相似度)进行推荐,获取某个商品的特征值
    val itemFactory=model.productFeatures.lookup(567).head
    val itemVector=new DoubleMatrix(itemFactory)
    //求余弦相似度
    val sim=model.productFeatures.map{
      case(id,factory)=>
        val factorVector=new DoubleMatrix(factory)
        val sim=cosineSimilarity(factorVector,itemVector)
        (id,sim)
    }
    val sortedsim=sim.top(11)(Ordering.by[(Int,Double),Double]{
      case(id,sim)=>sim
    })
    println(sortedsim.take(10).mkString("\n"))
    //模型评估,通过均误差
    //实际用户评估值
    val actualRatings=ratings.map{
      case Rating(user,item,rats) => ((user,item),rats)
    }
    val userItems=ratings.map{
      case(Rating(user,item,rats)) => (user,item)
    }
    //模型的用户对商品的预测值
    val predictRatings=model.predict(userItems).map{
      case(Rating(user,item,rats)) =>((user,item),rats)
    }
    //联合获取rate值
    val rates=actualRatings.join(predictRatings).map{
      case x =>(x._2._1,x._2._2)
    }
    //求均方差
    val regressionMetrics=new RegressionMetrics(rates)
    //越接近0越佳
    println(regressionMetrics.meanSquaredError)
    //全局平均准确率(MAP)
    val itemFactors = model.productFeatures.map { case (id, factor)
    => factor }.collect()
    val itemMatrix = new DoubleMatrix(itemFactors)
    //分布式广播商品的特征矩阵
    val imBroadcast = sc.broadcast(itemMatrix)
    //计算每一个用户的推荐,在这个操作里，会对用户因子矩阵和电影因子矩阵做乘积，其结果为一个表示各个电影预计评级的向量（长度为
    //1682，即电影的总数目）
    val allRecs = model.userFeatures.map{ case (userId, array) =>
      val userVector = new DoubleMatrix(array)
      val scores = imBroadcast.value.mmul(userVector)
      val sortedWithId = scores.data.zipWithIndex.sortBy(-_._1)
      val recommendedIds = sortedWithId.map(_._2 + 1).toSeq   //+1,矩阵从0开始
      (userId, recommendedIds)
    }
    //实际评分
    val userMovies = ratings.map{ case Rating(user, product, rating) =>
      (user, product)}.groupBy(_._1)
    val predictedAndTrueForRanking = allRecs.join(userMovies).map{ case
      (userId, (predicted, actualWithIds)) =>
      val actual = actualWithIds.map(_._2)
      (predicted.toArray, actual.toArray)
    }
    //求MAP,越大越好吧
    val rankingMetrics = new RankingMetrics(predictedAndTrueForRanking)
    println("Mean Average Precision = " + rankingMetrics.meanAveragePrecision)
  }
  //余弦相似度计算
  def cosineSimilarity(vec1:DoubleMatrix,vec2:DoubleMatrix):Double={
    vec1.dot(vec2)/(vec1.norm2()*vec2.norm2())
  }
}