[Algorithm] Fibonacci problem by using Dynamic programming

vThere are three ways to solve Fibonacci problem

1. Recursion
2. Memoize
3. Bottom-up

'First Recursion approach:

def fib(n):
    if n ==  or n == :
        result =
    else:
        result = fib(n-) + fib(n -)

    return result;

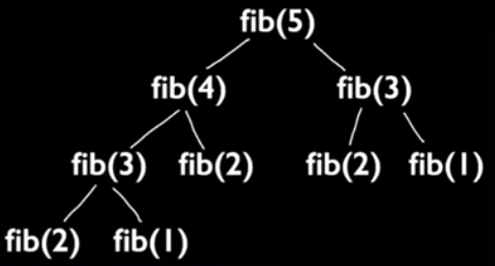
As we can see to calculate fib(5), we need to calculate fib(3) twice and fib(2) three times.

Time complexity is O(2^n), because for each n from 3, we need to call fib() twice in else block:

else:
    result = fib(n-) + fib(n -)

To solve the problem, we can use memoize solution to solve repeated calculation.

deb fib(n, memo):
    if memo[n] != null
        return memo[n]
    if n ==  or n == :
        result =
    else:
        result = fib(n - ) + fib(n-)
    memo[n] = result
    return result

Using fib(5) as example: to calulate fib(5) we need to know fib(4)..fib(3), fib(2), fib(1), since we already know fib(1), fib(2) = 1, then we can know fib(3) = 2..fib(4) = 3, fib(5) = 5.

Time complexity is O(2n + 1) -> O(n): because we just need to go though memo once. And 2*2 is because of:

result = fib(n - ) + fib(n-)

We still can improve it by using bottom up approach, because from the previous solution:

Using fib(5) as example: to calulate fib(5) we need to know fib(4)..fib(3), fib(2), fib(1), since we already know fib(1), fib(2) = 1, then we can know fib(3) = 2..fib(4) = 3, fib(5) = 5.

We can clear see the solution the problem by going from bottom (fib(1) & fib(2)) to up (fib(5)):

def fib_bottom_up(n):
    if n ==  or n == :
        return
    bottom_up = new int[n+]
    bottom_up[] =
    bottom_up[] =
    for i from  upto n:
        bottom_up[i] = bottom_up[i-]+bottom_up[i-]

    return bottom_up[n]

Time complexity is O(n).

---

Notice that some programming language has recursion limit, for example, python has set the limiation to 1000, which mean if you keep calling one function 1000 times, it will throw errors.

In this sense, bottom up is much better than recursion apporach (recursion and memoize).