LCT(link cut tree) 动态树
模板参考：https://blog.csdn.net/saramanda/article/details/55253627
综合各位大大博客后整理的模板：
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn = + ;
struct LCT
{
struct node
{
int fa, ch[]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子
int reverse;//区间反转标记
bool is_root; //是否是所在Splay的根
int siz;
}Tree[maxn];
int n; void init(int MN)
{
for (int i = ; i <= MN; i++)
{
Tree[i].reverse = Tree[i].fa = Tree[i].ch[] = Tree[i].ch[] = ;
Tree[i].is_root = true;
Tree[i].siz = ; }
} bool getson(int x)
{//x是否为重儿子
return x == Tree[Tree[x].fa].ch[];
}
bool isroot(int x)
{
return Tree[Tree[x].fa].ch[] != x && Tree[Tree[x].fa].ch[] != x;
}
void pushreverse(int x)
{
if (!x)return;
swap(Tree[x].ch[], Tree[x].ch[]);
Tree[x].reverse ^= ;
}
void pushdown(int x)
{//下传反转标记
if (Tree[x].reverse)
{
pushreverse(Tree[x].ch[]);
pushreverse(Tree[x].ch[]);
Tree[x].reverse = ;
}
} void update(int x)
{
int l = Tree[x].ch[], r = Tree[x].ch[];
Tree[x].siz = ;
if (l) Tree[x].siz += Tree[l].siz;
if (r) Tree[x].siz += Tree[r].siz;
} void rotate(int x)
{//将x旋转为根
if (Tree[x].is_root)return;
int k = getson(x), fa = Tree[x].fa;
int fafa = Tree[fa].fa;
pushdown(fa); pushdown(x); //先要下传标记
Tree[fa].ch[k] = Tree[x].ch[k ^ ];
if (Tree[x].ch[k ^ ])Tree[Tree[x].ch[k ^ ]].fa = fa;
Tree[x].ch[k ^ ] = fa;
Tree[fa].fa = x;
Tree[x].fa = fafa;
if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[]] = x;
else Tree[x].is_root = true, Tree[fa].is_root = false;
update(fa);update(x); //如果维护了信息，就要更新节点
}
void push(int x)
{
if (!Tree[x].is_root) push(Tree[x].fa);
pushdown(x);
}
int findroot(int x)
{//找到x在原树中的根节点
access(x); Splay(x);
pushdown(x);
while (Tree[x].ch[]) pushdown(x = Tree[x].ch[]);//找到深度最小的点即为根节点
return x;
}
void Splay(int x)
{//让x成为Splay的根，且x不含右儿子
push(x); //在Splay到根之前，必须先传完反转标记
for (int fa; !Tree[x].is_root; rotate(x)) {
if (!Tree[fa = Tree[x].fa].is_root) {
rotate((getson(x) == getson(fa)) ? fa : x);
}
}
}
void access(int x)
{//访问某节点。作用是：对于访问的节点x，打通一条从树根（真实的LCT树）到x的重链；如果x往下是重链，那么把x往下的重边改成轻边。结束后x没有右儿子（没有深度比他大的点）
int y = ;
do {
Splay(x);
Tree[Tree[x].ch[]].is_root = true;
Tree[Tree[x].ch[] = y].is_root = false;
update(x); //如果维护了信息记得更新。
x = Tree[y = x].fa;
} while (x);
}
void mroot(int x)
{//把某个节点变成树根（这里的根指的是整棵LCT的根）
access(x);//使x与根结点处在同一棵splay中
Splay(x);//x成为这棵splay的根,x只有左儿子
//由于根节点所在的splay中，根节点没有左儿子（没有深度比他小的节点），将x的左右子树翻转
pushreverse(x);
}
void link(int u, int v)
{//连接u所在的LCT和v所在的LCT
mroot(u);//先让u成为其所在LCT的根
if(findroot(v)!=u)Tree[u].fa = v;//如果u与v不在同一棵splay中，就把v设置为u的父亲
}
void cut(int u, int v)
{//分离出两棵LCT
mroot(u); //先让u成为其所在LCT的根
access(v); //让u和v在同一棵Splay中
Splay(v); //连接u、v，u是v的左儿子
pushdown(v); //先下传标记
if (Tree[v].ch[])
{
Tree[Tree[v].ch[]].fa = Tree[v].fa;
Tree[Tree[v].ch[]].is_root = true;
}
Tree[v].fa = ; Tree[v].ch[] = ;
//v的左孩子表示v上方相连的重链
update(v); //记得维护信息
} bool judge(int u, int v)
{//判断u和v是否连通
while (Tree[u].fa) u = Tree[u].fa;
while (Tree[v].fa) v = Tree[v].fa;
return u == v;
}
void split(int u, int v)
{//获取u->v的路径
mroot(u);//让u成为根结点
access(v);//访问v
Splay(v);//把v转到根结点，此时u的父亲为v
}
int Query_deep(int x)
{//询问x到LCT根的距离(深度)
access(x);
Splay(x);
return Tree[x].siz;
} void modify(int x,int v)
{//改变点值
access(x);
Splay(x);
//Tree[x].val = v;更改值
update(x); } }lct;
int main()
{ return ;
}
几个知识点：
1、LCT中用Splay维护链，这些Splay叫做“辅助树“。辅助树以它上面每个节点的深度为关键字维护，就是辅助树中每个节点左儿子的深度小于当前节点的深度，当前节点的深度小于右儿子的深度。
2、LCT相当于多棵splay被虚线连在一起，即splay森林；而最开始的时候是N个单独的点与他的父亲用虚线相连，每个点是一棵splay。
3、无论树怎样旋转，怎样变换，读入时所连接(link)的边（没有被cut的），一直都连着的
4、在每棵splay中每一个结点左子树中的节点都是他在原树中的祖先，右子树中的结点都是他在原树中的孩子。
5、splay森林实例：
原树：
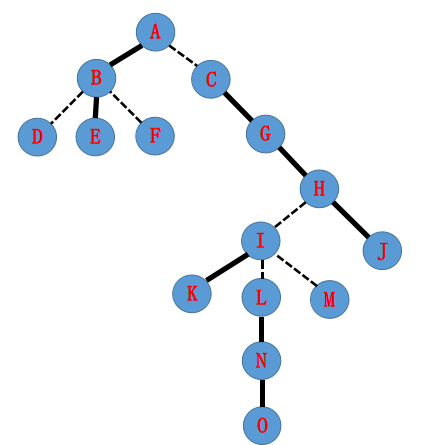
一种可能的splay森林：
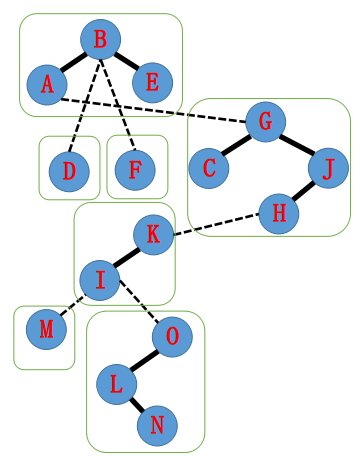
6、access(x)操作：
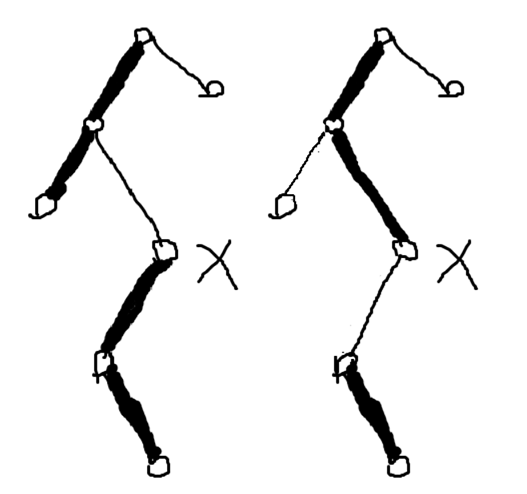
7、splay(x)操作：
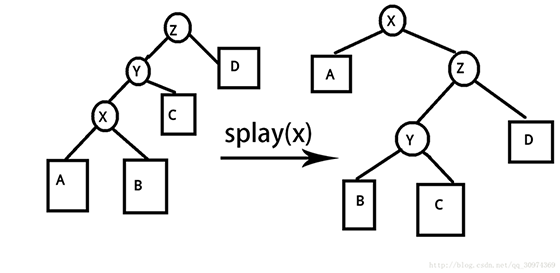
—————————题目—————————
1、Cave 洞穴勘测 HYSBZ - 2049
题意：一开始有n个洞穴，两两之间没有通道。每次将两个洞穴连接或者两个洞穴之间的通道摧毁，或者询问两个洞穴之间能否连通。
思路：LCT模板题。连接则通过link(u,v)实现，摧毁通过cut(u,v)实现，两个洞穴能否连通则考虑u的根和v的根是否相同。
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn = + ;
struct LCT
{
struct node
{
int fa, ch[]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子
int reverse;//区间反转标记
bool is_root; //是否是所在Splay的根
//int siz;
//int val;
//int sum;
}Tree[maxn];
int n;
//int v[maxn];//每个结点的值
void init()
{
for (int i = ; i <= n; i++)
{
Tree[i].reverse = Tree[i].fa = Tree[i].ch[] = Tree[i].ch[] = ;
Tree[i].is_root = true;
//Tree[i].siz = 1;
//Tree[i].val = Tree[i].sum = v[i];
}
} bool getson(int x)
{//x是否为重儿子
return x == Tree[Tree[x].fa].ch[];
}
bool isroot(int x)
{
return Tree[Tree[x].fa].ch[] != x && Tree[Tree[x].fa].ch[] != x;
}
void pushreverse(int x)
{
if (!x)return;
swap(Tree[x].ch[], Tree[x].ch[]);
Tree[x].reverse ^= ;
}
void pushdown(int x)
{//下传反转标记
if (Tree[x].reverse)
{
pushreverse(Tree[x].ch[]);
pushreverse(Tree[x].ch[]);
Tree[x].reverse = ;
}
}
/*
void update(int x)
{
int l = Tree[x].ch[0], r = Tree[x].ch[1];
Tree[x].siz = Tree[l].siz + Tree[r].siz + 1;
Tree[x].sum = Tree[l].sum + Tree[r].sum + Tree[x].val;
}
*/
void rotate(int x)
{//将x旋转为根
if (Tree[x].is_root)return;
int k = getson(x), fa = Tree[x].fa;
int fafa = Tree[fa].fa;
pushdown(fa); pushdown(x); //先要下传标记
Tree[fa].ch[k] = Tree[x].ch[k ^ ];
if (Tree[x].ch[k ^ ])Tree[Tree[x].ch[k ^ ]].fa = fa;
Tree[x].ch[k ^ ] = fa;
Tree[fa].fa = x;
Tree[x].fa = fafa;
if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[]] = x;
else Tree[x].is_root = true, Tree[fa].is_root = false;
//update(fa);update(x); //如果维护了信息，就要更新节点
}
void push(int x)
{
if (!Tree[x].is_root) push(Tree[x].fa);
pushdown(x);
}
int getFa(int x)
{//寻找x在原树的父亲
access(x);
Splay(x);
while (Tree[x].ch[]) x = Tree[x].ch[];
return x;
}
void Splay(int x)
{//让x成为Splay的根
push(x); //在Splay到根之前，必须先传完反转标记
for (int fa; !Tree[x].is_root; rotate(x)) {
if (!Tree[fa = Tree[x].fa].is_root) {
rotate((getson(x) == getson(fa)) ? fa : x);
}
}
}
void access(int x)
{//访问某节点。作用是：对于访问的节点x，打通一条从树根（真实的LCT树）到x的重链；如果x往下是重链，那么把x往下的重边改成轻边。
int y = ;
do {
Splay(x);
Tree[Tree[x].ch[]].is_root = true;
Tree[Tree[x].ch[] = y].is_root = false;
//update(x); //如果维护了信息记得更新。
x = Tree[y = x].fa;
} while (x);
}
void mroot(int x)
{//把某个节点变成树根（这里的根指的是整棵LCT的根）
access(x);//使x与根结点处在同一棵splay中
Splay(x);//x成为这棵splay的根,x只有左儿子
pushreverse(x);
}
void link(int u, int v)
{//连接u所在的LCT和v所在的LCT
mroot(u);//先让u成为其所在LCT的根
Tree[u].fa = v;
}
void cut(int u, int v)
{//分离出两棵LCT
mroot(u); //先让u成为其所在LCT的根
access(v); //让u和v在同一棵Splay中
Splay(v); //连接u、v，u是v的左儿子
pushdown(v); //先下传标记
Tree[Tree[v].ch[]].fa = Tree[v].fa;
Tree[Tree[v].ch[]].is_root = true;
Tree[v].fa = ;
Tree[v].ch[] = ;
//v的左孩子表示v上方相连的重链
//update(v); //记得维护信息
}
bool judge(int u, int v)
{//判断u和v是否连通
while (Tree[u].fa) u = Tree[u].fa;
while (Tree[v].fa) v = Tree[v].fa;
return u == v;
}
}lct;
int main()
{
int m;
while (~scanf("%d%d", &lct.n, &m))
{
lct.init();
char op[];
int u, v;
for (int i = ; i <= m; i++)
{
scanf("%s%d%d", op, &u, &v);
if (op[] == 'Q')
{
if (lct.judge(u, v)) printf("Yes\n");
else printf("No\n");
}
else if (op[] == 'C')
{
lct.link(u, v);
}
else
{
lct.cut(u, v);
}
}
}
return ;
}
2、Bounce 弹飞绵羊 HYSBZ - 2002
题意：有n个弹射装置，当绵羊在第i个弹射装置时，会被弹射到第i+val[i]个弹射装置，val数组记录每个弹射装置的弹射系数。有两个操作，要么询问当绵羊站在第x个弹射装置时会经过多少次被弹飞，要么修改某个弹射装置的系数。
思路：可以将第i个弹射装置与第i+val[i]个装置相连，新增第n+1个点作为树根，表示被弹飞。询问次数时即询问当前x到树根的距离即深度，然后-1即可（第n+1个结点不弹射）；修改某个弹射装置的系数相当于修改某个结点的父亲，先将原父亲删除，再重新连接父亲。
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = + ;
int val[maxn];
struct LCT
{
struct node
{
int fa, ch[]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子
int reverse;//区间反转标记
bool is_root; //是否是所在Splay的根
int siz;
}Tree[maxn];
int n;
void init(int maxn)
{
for (int i = ; i <= maxn; i++)
{
Tree[i].reverse = Tree[i].fa = Tree[i].ch[] = Tree[i].ch[] = ;
Tree[i].is_root = true;
Tree[i].siz = ;
}
} bool getson(int x)
{//x是否为重儿子
return x == Tree[Tree[x].fa].ch[];
}
bool isroot(int x)
{
return Tree[Tree[x].fa].ch[] != x && Tree[Tree[x].fa].ch[] != x;
}
void pushreverse(int x)
{
if (!x)return;
swap(Tree[x].ch[], Tree[x].ch[]);
Tree[x].reverse ^= ;
}
void pushdown(int x)
{//下传反转标记
if (Tree[x].reverse)
{
pushreverse(Tree[x].ch[]);
pushreverse(Tree[x].ch[]);
Tree[x].reverse = ;
}
} void update(int x)
{
int l = Tree[x].ch[], r = Tree[x].ch[];
Tree[x].siz = ;
if (l) Tree[x].siz += Tree[l].siz;
if (r) Tree[x].siz += Tree[r].siz;
} void rotate(int x)
{//将x旋转为根
if (Tree[x].is_root)return;
int k = getson(x), fa = Tree[x].fa;
int fafa = Tree[fa].fa;
pushdown(fa); pushdown(x); //先要下传标记
Tree[fa].ch[k] = Tree[x].ch[k ^ ];
if (Tree[x].ch[k ^ ])Tree[Tree[x].ch[k ^ ]].fa = fa;
Tree[x].ch[k ^ ] = fa;
Tree[fa].fa = x;
Tree[x].fa = fafa;
if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[]] = x;
else Tree[x].is_root = true, Tree[fa].is_root = false;
update(fa);update(x); //如果维护了信息，就要更新节点
}
void push(int x)
{
if (!Tree[x].is_root) push(Tree[x].fa);
pushdown(x);
}
int getFa(int x)
{//寻找x在原树的父亲
access(x);
Splay(x);
while (Tree[x].ch[]) x = Tree[x].ch[];
return x;
}
void Splay(int x)
{//让x成为Splay的根
push(x); //在Splay到根之前，必须先传完反转标记
for (int fa; !Tree[x].is_root; rotate(x)) {
if (!Tree[fa = Tree[x].fa].is_root) {
rotate((getson(x) == getson(fa)) ? fa : x);
}
}
}
void access(int x)
{//访问某节点。作用是：对于访问的节点x，打通一条从树根（真实的LCT树）到x的重链；如果x往下是重链，那么把x往下的重边改成轻边。
int y = ;
do {
Splay(x);
Tree[Tree[x].ch[]].is_root = true;
Tree[Tree[x].ch[] = y].is_root = false;
update(x); //如果维护了信息记得更新。
x = Tree[y = x].fa;
} while (x);
}
void mroot(int x)
{//把某个节点变成树根（这里的根指的是整棵LCT的根）
access(x);//使x与根结点处在同一棵splay中
Splay(x);//x成为这棵splay的根,x只有左儿子
pushreverse(x);
}
void link(int u, int v)
{//连接u所在的LCT和v所在的LCT
mroot(u);//先让u成为其所在LCT的根
Tree[u].fa = v;
Tree[u].is_root = true;
}
void cut(int u, int v)
{//分离出两棵LCT
mroot(u); //先让u成为其所在LCT的根
access(v); //让u和v在同一棵Splay中
Splay(v); //连接u、v，u是v的左儿子
pushdown(v); //先下传标记
Tree[Tree[v].ch[]].fa = Tree[v].fa;
Tree[Tree[v].ch[]].is_root = true;
Tree[v].fa = ;
Tree[v].ch[] = ;
//v的左孩子表示v上方相连的重链
update(v); //记得维护信息
}
bool judge(int u, int v)
{//判断u和v是否连通
while (Tree[u].fa) u = Tree[u].fa;
while (Tree[v].fa) v = Tree[v].fa;
return u == v;
}
int Query_deep(int x)
{//询问x到LCT根的距离(深度)
access(x);
Splay(x);
return Tree[x].siz;
}
}lct;
int main()
{
int m;
while (~scanf("%d", &lct.n))
{
lct.init(lct.n+);////让n+1表示被弹飞
for (int i = ; i <= lct.n; i++)
{
scanf("%d", &val[i]);
int id = min(i + val[i], lct.n + );
lct.link(i, id);
}
lct.mroot(lct.n + );
scanf("%d", &m);
for (int i = ; i <= m; i++)
{
int op, x;
scanf("%d%d", &op, &x);
x++;
if (op == ) printf("%d\n", lct.Query_deep(x)-);
else
{
int v;
scanf("%d", &v);
int oid = min(x + val[x], lct.n + );
int nid = min(x + v, lct.n + );
lct.cut(x, oid);
lct.link(x, nid);
lct.mroot(lct.n + );
val[x] = v;
}
}
}
return ;
}
3、魔法森林 HYSBZ - 3669
题意：有一个无向图，起点在1，终点在n.每条边有两个权值ai、bi，当且仅当从1到n的路径过程中，身上a的数目不小于路径上的任一条边，b的数目也不小于路径上的任一条边。求最小的a+b。
思路：先将所有边对ai从小到大排序，把所有边拆成两条边插入LCT，自身边权用新的点的点权表示。LCT中结点维护当前splay树中最大的bi以及对应的结点编号。各个结点的连通性用并查集维护。如果对于枚举到的边，其端点之间不连通，则将其拆成1个新的结点和两条边插入LCT；否则，得到该splay中最大的maxb(从splay的根结点得到)，以及其对应的边所映射的点的编号（num），如果当前边的bi更小，则需要将原来的边删除，将该边插入（注意，因为把一条边拆成两条边，所以各需要操作两次）。判断结束后，如果当前情形下，起点和终点连通，则更新ans=min(ans,maxb+当前枚举边的ai)。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = + ;
const int maxm = + ;
const int INF = 0x7f7f7f7f;
struct EDGE
{
int from, to, a, b;
EDGE(int ff=,int tt=,int aa=,int bb=){}
friend bool operator <(const EDGE&e1, const EDGE&e2)
{
return e1.a < e2.a;
}
}edge[maxm];
int m,n;
//并查集,维护连通性
int pre[maxn + maxm];
int Find(int x)
{
if (pre[x] == x) return x;
else
{
int fa = pre[x];
pre[x] = Find(fa);
return pre[x];
}
} struct LCT
{
struct node
{
int fa, ch[]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子
int reverse;//区间反转标记
bool is_root; //是否是所在Splay的根
int siz;//子树结点数目
int maxb, num, bi;//splay中最大的bi、与之对应的结点编号、当前结点的bi
}Tree[maxn+maxm]; void init(int MN)
{
for (int i = ; i <= MN; i++)
{
Tree[i].reverse = Tree[i].fa = Tree[i].ch[] = Tree[i].ch[] = ;
Tree[i].is_root = true;
Tree[i].num = i;
Tree[i].siz = ;
if (i <= n) Tree[i].maxb = Tree[i].bi = ;
else
{
Tree[i].maxb = Tree[i].bi = edge[i - n].b;
}
pre[i] = i;
}
} bool getson(int x)
{//x是否为重儿子
return x == Tree[Tree[x].fa].ch[];
}
bool isroot(int x)
{
return Tree[Tree[x].fa].ch[] != x && Tree[Tree[x].fa].ch[] != x;
}
void pushreverse(int x)
{
if (!x)return;
swap(Tree[x].ch[], Tree[x].ch[]);
Tree[x].reverse ^= ;
}
void pushdown(int x)
{//下传反转标记
if (Tree[x].reverse)
{
pushreverse(Tree[x].ch[]);
pushreverse(Tree[x].ch[]);
Tree[x].reverse = ;
}
} void update(int x)
{
int l = Tree[x].ch[], r = Tree[x].ch[];
Tree[x].siz = ;
Tree[x].maxb = Tree[x].bi;
Tree[x].num = x;
if (l)
{
Tree[x].siz += Tree[l].siz;
if (Tree[l].maxb > Tree[x].maxb) Tree[x].maxb = Tree[l].maxb, Tree[x].num = Tree[l].num;
}
if (r)
{
Tree[x].siz += Tree[r].siz;
if (Tree[r].maxb > Tree[x].maxb) Tree[x].maxb = Tree[r].maxb, Tree[x].num = Tree[r].num;
} } void rotate(int x)
{//将x旋转为根
if (Tree[x].is_root)return;
int k = getson(x), fa = Tree[x].fa;
int fafa = Tree[fa].fa;
pushdown(fa); pushdown(x); //先要下传标记
Tree[fa].ch[k] = Tree[x].ch[k ^ ];
if (Tree[x].ch[k ^ ])Tree[Tree[x].ch[k ^ ]].fa = fa;
Tree[x].ch[k ^ ] = fa;
Tree[fa].fa = x;
Tree[x].fa = fafa;
if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[]] = x;
else Tree[x].is_root = true, Tree[fa].is_root = false;
update(fa); update(x); //如果维护了信息，就要更新节点
}
void push(int x)
{
if (!Tree[x].is_root) push(Tree[x].fa);
pushdown(x);
}
int findroot(int x)
{//找到x在原树中的根节点
access(x); Splay(x);
pushdown(x);
while (Tree[x].ch[]) pushdown(x = Tree[x].ch[]);//找到深度最小的点即为根节点
return x;
}
void Splay(int x)
{//让x成为Splay的根，且x不含右儿子
push(x); //在Splay到根之前，必须先传完反转标记
for (int fa; !Tree[x].is_root; rotate(x)) {
if (!Tree[fa = Tree[x].fa].is_root) {
rotate((getson(x) == getson(fa)) ? fa : x);
}
}
}
void access(int x)
{//访问某节点。作用是：对于访问的节点x，打通一条从树根（真实的LCT树）到x的重链；如果x往下是重链，那么把x往下的重边改成轻边。结束后x没有右儿子（没有深度比他大的点）
int y = ;
do {
Splay(x);
Tree[Tree[x].ch[]].is_root = true;
Tree[Tree[x].ch[] = y].is_root = false;
update(x); //如果维护了信息记得更新。
x = Tree[y = x].fa;
} while (x);
}
void mroot(int x)
{//把某个节点变成树根（这里的根指的是整棵LCT的根）
access(x);//使x与根结点处在同一棵splay中
Splay(x);//x成为这棵splay的根,x只有左儿子
//由于根节点所在的splay中，根节点没有左儿子（没有深度比他小的节点），将x的左右子树翻转
pushreverse(x);
}
void link(int u, int v)
{//连接u所在的LCT和v所在的LCT
mroot(u);//先让u成为其所在LCT的根
if (findroot(v) != u)Tree[u].fa = v;//如果u与v不在同一棵splay中，就把v设置为u的父亲
}
void cut(int u, int v)
{//分离出两棵LCT
mroot(u); //先让u成为其所在LCT的根
access(v); //让u和v在同一棵Splay中
Splay(v); //连接u、v，u是v的左儿子
pushdown(v); //先下传标记
if (Tree[v].ch[])
{
Tree[Tree[v].ch[]].fa = Tree[v].fa;
Tree[Tree[v].ch[]].is_root = true;
}
Tree[v].fa = ; Tree[v].ch[] = ;
//v的左孩子表示v上方相连的重链
update(v); //记得维护信息
} bool judge(int u, int v)
{//判断u和v是否连通
while (Tree[u].fa) u = Tree[u].fa;
while (Tree[v].fa) v = Tree[v].fa;
return u == v;
}
void split(int u, int v)
{//获取u->v的路径
mroot(u);//让u成为根结点
access(v);//访问v
Splay(v);//把v转到根结点，此时u的父亲为v
}
int Query_deep(int x)
{//询问x到LCT根的距离(深度)
access(x);
Splay(x);
return Tree[x].siz;
} }lct;
int main()
{
while (~scanf("%d%d", &n, &m))
{
for (int i = ; i <= m; i++)
{
scanf("%d%d%d%d", &edge[i].from, &edge[i].to, &edge[i].a, &edge[i].b);
}
sort(edge + , edge + + m);
lct.init(n+m); int ans = INF;
for (int i = ; i <= m; i++)
{
if (edge[i].from == edge[i].to)continue;
int f_from = Find(edge[i].from),f_to = Find(edge[i].to);
if (f_from != f_to)
{//不连通
lct.link(edge[i].from, i + n);//把一条边拆成2条边和一个点，化作点权
lct.link(edge[i].to, i + n);
pre[f_to] = pre[f_from] = Find(i + n);
}
else
{//连通
lct.split(edge[i].from, edge[i].to);
int x = lct.Tree[edge[i].to].num;
if (edge[i].b < lct.Tree[x].bi)
{
lct.cut(edge[i].from, x);
lct.cut(edge[i].to, x);
lct.link(edge[i].from, i + n);
lct.link(edge[i].to, i + n);
}
}
if (Find() == Find(n))
{
lct.split(, n);
ans = min(ans, lct.Tree[n].maxb + edge[i].a);
}
}
if (ans != INF) printf("%d\n", ans);
else printf("-1\n");
}
return ;
}
4、spoj 4155 OTOCI
题意：有n座小岛，一开始两两之间没有桥，每座岛上有若干只企鹅。有三种操作：修改某座岛上的企鹅数目；将某两座岛相连；询问从一座岛到另一座岛路径上所有的企鹅数目。
思路：用LCT维护某座岛的值和子树和。
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn = + ;
int n;
struct LCT
{
struct node
{
int fa, ch[]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子
int reverse;//区间反转标记
bool is_root; //是否是所在Splay的根
int val;
int sum;
}Tree[maxn]; void init(int MN)
{
for (int i = ; i <= MN; i++)
{
Tree[i].reverse = Tree[i].fa = Tree[i].ch[] = Tree[i].ch[] = ;
Tree[i].is_root = true;
}
} bool getson(int x)
{//x是否为重儿子
return x == Tree[Tree[x].fa].ch[];
}
bool isroot(int x)
{
return Tree[Tree[x].fa].ch[] != x && Tree[Tree[x].fa].ch[] != x;
}
void pushreverse(int x)
{
if (!x)return;
swap(Tree[x].ch[], Tree[x].ch[]);
Tree[x].reverse ^= ;
}
void pushdown(int x)
{//下传反转标记
if (Tree[x].reverse)
{
pushreverse(Tree[x].ch[]);
pushreverse(Tree[x].ch[]);
Tree[x].reverse = ;
}
} void update(int x)
{
int l = Tree[x].ch[], r = Tree[x].ch[];
Tree[x].sum = Tree[x].val;
if (l) Tree[x].sum += Tree[l].sum;
if (r) Tree[x].sum += Tree[r].sum;
} void rotate(int x)
{//将x旋转为根
if (Tree[x].is_root)return;
int k = getson(x), fa = Tree[x].fa;
int fafa = Tree[fa].fa;
pushdown(fa); pushdown(x); //先要下传标记
Tree[fa].ch[k] = Tree[x].ch[k ^ ];
if (Tree[x].ch[k ^ ])Tree[Tree[x].ch[k ^ ]].fa = fa;
Tree[x].ch[k ^ ] = fa;
Tree[fa].fa = x;
Tree[x].fa = fafa;
if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[]] = x;
else Tree[x].is_root = true, Tree[fa].is_root = false;
update(fa); update(x); //如果维护了信息，就要更新节点
}
void push(int x)
{
if (!Tree[x].is_root) push(Tree[x].fa);
pushdown(x);
}
int findroot(int x)
{//找到x在原树中的根节点
access(x); Splay(x);
pushdown(x);
while (Tree[x].ch[]) pushdown(x = Tree[x].ch[]);//找到深度最小的点即为根节点
return x;
}
void Splay(int x)
{//让x成为Splay的根，且x不含右儿子
push(x); //在Splay到根之前，必须先传完反转标记
for (int fa; !Tree[x].is_root; rotate(x)) {
if (!Tree[fa = Tree[x].fa].is_root) {
rotate((getson(x) == getson(fa)) ? fa : x);
}
}
}
void access(int x)
{//访问某节点。作用是：对于访问的节点x，打通一条从树根（真实的LCT树）到x的重链；如果x往下是重链，那么把x往下的重边改成轻边。结束后x没有右儿子（没有深度比他大的点）
int y = ;
do {
Splay(x);
Tree[Tree[x].ch[]].is_root = true;
Tree[Tree[x].ch[] = y].is_root = false;
update(x); //如果维护了信息记得更新。
x = Tree[y = x].fa;
} while (x);
}
void mroot(int x)
{//把某个节点变成树根（这里的根指的是整棵LCT的根）
access(x);//使x与根结点处在同一棵splay中
Splay(x);//x成为这棵splay的根,x只有左儿子
//由于根节点所在的splay中，根节点没有左儿子（没有深度比他小的节点），将x的左右子树翻转
pushreverse(x);
}
void link(int u, int v)
{//连接u所在的LCT和v所在的LCT
mroot(u);//先让u成为其所在LCT的根
if (findroot(v) != u)Tree[u].fa = v;//如果u与v不在同一棵splay中，就把v设置为u的父亲 }
void cut(int u, int v)
{//分离出两棵LCT
mroot(u); //先让u成为其所在LCT的根
access(v); //让u和v在同一棵Splay中
Splay(v); //连接u、v，u是v的左儿子
pushdown(v); //先下传标记
if (Tree[v].ch[])
{
Tree[Tree[v].ch[]].fa = Tree[v].fa;
Tree[Tree[v].ch[]].is_root = true;
}
Tree[v].fa = ; Tree[v].ch[] = ;
//v的左孩子表示v上方相连的重链
update(v); //记得维护信息
} bool judge(int u, int v)
{//判断u和v是否连通
while (Tree[u].fa) u = Tree[u].fa;
while (Tree[v].fa) v = Tree[v].fa;
return u == v;
}
void split(int u, int v)
{//获取u->v的路径
mroot(u);//让u成为根结点
access(v);//访问v
Splay(v);//把v转到根结点，此时u的父亲为v,u是v的左儿子
} void modify(int x, int v)
{//改变点值
access(x);
Splay(x);
Tree[x].val = v;
update(x);
} }lct;
int main()
{
scanf("%d", &n);
lct.init(n);
for (int i = ; i <= n; i++)
{
scanf("%d", &lct.Tree[i].val);
lct.Tree[i].sum = lct.Tree[i].val;
}
int m;
scanf("%d", &m);
char op[];
while (m--)
{
scanf("%s", op);
if (op[] == 'e')
{
int u, v;
scanf("%d%d", &u, &v);
if (lct.judge(u, v))
{
lct.split(u, v);
printf("%d\n", lct.Tree[v].sum );
}
else
{
printf("impossible\n");
}
}
else if (op[] == 'b')
{
int u, v;
scanf("%d%d", &u, &v);
if (!lct.judge(u, v))
{
printf("yes\n");
lct.link(u, v);
}
else printf("no\n");
}
else
{
int u, w;
scanf("%d%d", &u, &w);
lct.modify(u, w);
}
}
return ;
}
5、Caves and Tunnels URAL - 1553
题意：有n个洞穴，由n-1条通道相连。有两种操作：将某个洞穴的辐射水平升高一定值；询问两个洞穴之间最大的辐射值。
思路：LCT维护当前结点的辐射值以及子树的最大辐射值。亦可以使用树链剖分来解决，因为没有链的变动，其实是个静态树。
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int maxn = + ;
int n, q;
struct LCT
{
struct node
{
int fa, ch[]; //父亲(Splay对应的链向上由轻边连着哪个节点)、左右儿子
int reverse;//区间反转标记
bool is_root; //是否是所在Splay的根
int val;
int maxv;
}Tree[maxn]; void init(int MN)
{
for (int i = ; i <= MN; i++)
{
Tree[i].reverse = Tree[i].fa = Tree[i].ch[] = Tree[i].ch[] = ;
Tree[i].is_root = true;
Tree[i].val = Tree[i].maxv = ;
}
} bool getson(int x)
{//x是否为重儿子
return x == Tree[Tree[x].fa].ch[];
}
bool isroot(int x)
{
return Tree[Tree[x].fa].ch[] != x && Tree[Tree[x].fa].ch[] != x;
}
void pushreverse(int x)
{
if (!x)return;
swap(Tree[x].ch[], Tree[x].ch[]);
Tree[x].reverse ^= ;
}
void pushdown(int x)
{//下传反转标记
if (Tree[x].reverse)
{
pushreverse(Tree[x].ch[]);
pushreverse(Tree[x].ch[]);
Tree[x].reverse = ;
}
} void update(int x)
{
int l = Tree[x].ch[], r = Tree[x].ch[];
Tree[x].maxv = Tree[x].val;
if (l) Tree[x].maxv = max(Tree[x].maxv, Tree[l].maxv);
if (r) Tree[x].maxv = max(Tree[x].maxv, Tree[r].maxv);
} void rotate(int x)
{//将x旋转为根
if (Tree[x].is_root)return;
int k = getson(x), fa = Tree[x].fa;
int fafa = Tree[fa].fa;
pushdown(fa); pushdown(x); //先要下传标记
Tree[fa].ch[k] = Tree[x].ch[k ^ ];
if (Tree[x].ch[k ^ ])Tree[Tree[x].ch[k ^ ]].fa = fa;
Tree[x].ch[k ^ ] = fa;
Tree[fa].fa = x;
Tree[x].fa = fafa;
if (!Tree[fa].is_root)Tree[fafa].ch[fa == Tree[fafa].ch[]] = x;
else Tree[x].is_root = true, Tree[fa].is_root = false;
update(fa); update(x); //如果维护了信息，就要更新节点
}
void push(int x)
{
if (!Tree[x].is_root) push(Tree[x].fa);
pushdown(x);
}
int findroot(int x)
{//找到x在原树中的根节点
access(x); Splay(x);
pushdown(x);
while (Tree[x].ch[]) pushdown(x = Tree[x].ch[]);//找到深度最小的点即为根节点
return x;
}
void Splay(int x)
{//让x成为Splay的根，且x不含右儿子
push(x); //在Splay到根之前，必须先传完反转标记
for (int fa; !Tree[x].is_root; rotate(x)) {
if (!Tree[fa = Tree[x].fa].is_root) {
rotate((getson(x) == getson(fa)) ? fa : x);
}
}
}
void access(int x)
{//访问某节点。作用是：对于访问的节点x，打通一条从树根（真实的LCT树）到x的重链；如果x往下是重链，那么把x往下的重边改成轻边。结束后x没有右儿子（没有深度比他大的点）
int y = ;
do {
Splay(x);
Tree[Tree[x].ch[]].is_root = true;
Tree[Tree[x].ch[] = y].is_root = false;
update(x); //如果维护了信息记得更新。
x = Tree[y = x].fa;
} while (x);
}
void mroot(int x)
{//把某个节点变成树根（这里的根指的是整棵LCT的根）
access(x);//使x与根结点处在同一棵splay中
Splay(x);//x成为这棵splay的根,x只有左儿子
//由于根节点所在的splay中，根节点没有左儿子（没有深度比他小的节点），将x的左右子树翻转
pushreverse(x);
}
void link(int u, int v)
{//连接u所在的LCT和v所在的LCT
mroot(u);//先让u成为其所在LCT的根
if (findroot(v) != u)Tree[u].fa = v;//如果u与v不在同一棵splay中，就把v设置为u的父亲
}
void cut(int u, int v)
{//分离出两棵LCT
mroot(u); //先让u成为其所在LCT的根
access(v); //让u和v在同一棵Splay中
Splay(v); //连接u、v，u是v的左儿子
pushdown(v); //先下传标记
if (Tree[v].ch[])
{
Tree[Tree[v].ch[]].fa = Tree[v].fa;
Tree[Tree[v].ch[]].is_root = true;
}
Tree[v].fa = ; Tree[v].ch[] = ;
//v的左孩子表示v上方相连的重链
update(v); //记得维护信息
} bool judge(int u, int v)
{//判断u和v是否连通
while (Tree[u].fa) u = Tree[u].fa;
while (Tree[v].fa) v = Tree[v].fa;
return u == v;
}
void split(int u, int v)
{//获取u->v的路径
mroot(u);//让u成为根结点
access(v);//访问v
Splay(v);//把v转到根结点，此时u的父亲为v
} void modify(int x, int v)
{//改变点值
access(x);
Splay(x);
Tree[x].val += v;
update(x); } }lct;
char op[];
int main()
{
scanf("%d", &n);
lct.init(n);
for (int i = ; i <= n - ; i++)
{
int u, v;
scanf("%d%d", &u, &v);
lct.link(u, v);
}
scanf("%d", &q);
while (q--)
{
scanf("%s", op);
if (op[] == 'I')
{
int u, w;
scanf("%d%d", &u, &w);
lct.modify(u, w);
}
else
{
int u, v;
scanf("%d%d", &u, &v);
lct.split(u, v);
printf("%d\n", lct.Tree[v].maxv);
}
}
return ;
}
LCT(link cut tree) 动态树的更多相关文章
- LCT总结——概念篇+洛谷P3690[模板]Link Cut Tree(动态树)（LCT，Splay）
为了优化体验(其实是强迫症),蒟蒻把总结拆成了两篇,方便不同学习阶段的Dalao们切换. LCT总结--应用篇戳这里 概念.性质简述 首先介绍一下链剖分的概念(感谢laofu的讲课) 链剖分,是指一类 ...
- Link Cut Tree 动态树 小结
动态树有些类似 树链剖分+并查集 的思想,是用splay维护的 lct的根是动态的,"轻重链"也是动态的,所以并没有真正的轻重链 动态树的操作核心是把你要把 修改/询问/... 等 ...
- 洛谷.3690.[模板]Link Cut Tree(动态树)
题目链接 LCT(良心总结) #include <cstdio> #include <cctype> #include <algorithm> #define gc ...
- 洛谷P3690 Link Cut Tree (动态树)
干脆整个LCT模板吧. 缺个链上修改和子树操作,链上修改的话join(u,v)然后把v splay到树根再打个标记就好. 至于子树操作...以后有空的话再学(咕咕咕警告) #include<bi ...
- 【学习笔记】LCT link cut tree
大概就是供自己复习的吧 1. 细节讲解 安利两篇blog: Menci 非常好的讲解与题单 2.模板 把 $ rev $ 和 $ pushdown $ 的位置记清 #define lc son[x][ ...
- 【刷题】洛谷 P3690 【模板】Link Cut Tree （动态树）
题目背景 动态树 题目描述 给定n个点以及每个点的权值,要你处理接下来的m个操作.操作有4种.操作从0到3编号.点从1到n编号. 0:后接两个整数(x,y),代表询问从x到y的路径上的点的权值的xor ...
- LuoguP3690 【模板】Link Cut Tree （动态树） LCT模板
P3690 [模板]Link Cut Tree (动态树) 题目背景 动态树 题目描述 给定n个点以及每个点的权值,要你处理接下来的m个操作.操作有4种.操作从0到3编号.点从1到n编号. 0:后接两 ...
- P3690 【模板】Link Cut Tree （动态树）
P3690 [模板]Link Cut Tree (动态树) 认父不认子的lct 注意:不 要 把 $fa[x]$和$nrt(x)$ 混 在 一 起 ! #include<cstdio> v ...
- LG3690 【模板】Link Cut Tree （动态树）
题意 给定n个点以及每个点的权值,要你处理接下来的m个操作.操作有4种.操作从0到3编号.点从1到n编号. 0:后接两个整数(x,y),代表询问从x到y的路径上的点的权值的xor和.保证x到y是联通的 ...
随机推荐
- 解决 Visual Studio For Mac 还原包失败问题
体验了一把改名部最新的杰作,总体感觉挺好,也能看出微软在跨平台这方面所做出的努力. 可能是预览版的缘故,还是遇到一个比较大的问题,创建netcore项目后,依赖包还原失败,错误信息如下: 可以先试着手 ...
- python管理工具easy_install与pip
刚开始同步系统的接触python和linux,在昊妹妹的指引下学习了使用python管理工具,希望能够通过不断熟练来学习 1.记录之前先复习以下linux下常用目录 ./ 表示当前目录 ~/ 表示h ...
- Java逍遥游记读书笔记<一>
前言 必须先来一句,这是入门级别,高手勿喷~ 写Android的时候总有一些语句不是很理解,其实大部分是Java的内容,所以想系统的学下Java. 这本书——<Java逍遥游记>是在图书馆 ...
- 【转】Android横竖屏重力自适应
通常我们的应用只会设计成横屏或者竖屏,锁定横屏或竖屏的方法是在manifest.xml文件中设定属性android:screenOrientation为"landscape"或&q ...
- js和jquery获取父级元素、子级元素、兄弟元素的方法{转}
先说一下JS的获取方法,其要比JQUERY的方法麻烦很多,后面以JQUERY的方法作对比 JS的方法会比JQUERY麻烦很多,主要则是因为FF浏览器,FF浏览器会把你的换行也当成DOM元素 原生的 ...
- Innodb间隙锁，细节讲解（转）
关于innodb间隙锁,网上有很多资料,在此不做赘述,我们讲解一下关于innodb的间隙锁什么情况下会产生的问题. 网上有些资料说innodb的间隙锁是为了防止幻读,这个论点真的是误人子弟.了解inn ...
- python 之 多进程
阅读目录 1. Process 2. Lock 3. Semaphore 4. Event 5. Queue 6. Pipe 7. Pool 序. multiprocessingpython中的多线程 ...
- 《ASP.NET 1200例》ref关键字与out关键字
REF关键字 ref 关键字会导致通过引用传递的参数,而不是值. 通过引用传递的效果是在方法中对参数的任何改变都会反映在调用方的基础参数中. 引用参数的值与基础参数变量的值始终是一样的. 不要将“通过 ...
- 数据结构 + 算法 -> 收集
董的博客:数据机构与算法合集 背包问题应用(2011-08-26) 数据结构之红黑树(2011-08-20) 素数判定算法(2011-06-26) 算法之图搜索算法(一)(2011-06-22) 算法 ...
- OpenvSwitch2.4.0源码解读
原文发表在我的博客主页,转载请注明出处! 一.前言 OpenvSwitch,虚拟交换机,以下简称OVS,是云计算和SDN领域非常重要的一个开源交换机,如果需要深入研究云计算和SDN的数据平面,读懂OV ...