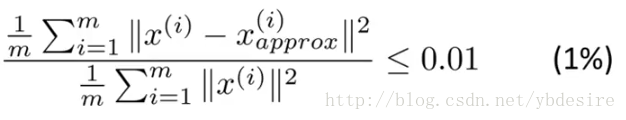PCA误差
我们知道,PCA是用于对数据做降维的,我们一般用PCA把m维的数据降到k维(k < m)。
那么问题来了,k取值多少才合适呢?
PCA误差
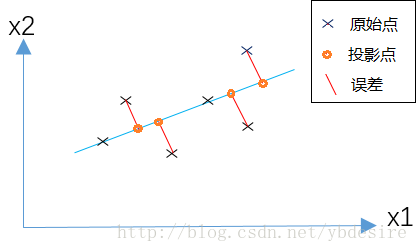
PCA的原理是,为了将数据从n维降低到k维,需要找到k个向量,用于投影原始数据,是投影误差(投影距离)最小。
用公式来表示,如下
其中
- m表示特征个数
分子表示原始点与投影点之间的距离之和,而误差越小,说明降维后的数据越能完整表示降维前的数据。如果这个误差小于0.01,说明降维后的数据能保留99%的信息。
k值选取的原理
实际应用中,我们一般根据上式,选择能使误差小于0.01(99%的信息都被保留)或0.05(95%的信息都被保留)的k值。
而在实际编码中,参考文章《详解主成分分析PCA》,在PCA的实现过程中,对协方差矩阵做奇异值分解时,能得到S矩阵(特征值矩阵)。
PCA误差的表达式等效于下式
从代码示例中,可以看出,将数据从三维降到二维,保留了99.997%的信息。
[U,S,V] = np.linalg.svd(sigma) # 奇异值分解(S[0]+S[1])/(S www.hbs90.cn/ www.boshenyl.cn [0]+S[1]+S[2])# result = 0.99996991682077252
- 1
- 2
- 3
实际使用
用sklearn封装的PCA方法,做PCA的代码如下。PCA方法参数n_components,如果设置为整数,则n_components=k。如果将其设置为小数,则说明降维后的数据能保留的信息。
from sklearn.decomposition import PCAimport numpy as npfrom sklearn.preprocessing import StandardScalerx=np.array([[10001,2,55],www.feihuanyule.com [16020,4,11], [12008,6,33], [13131,8,22]])# feature normalization (feature scaling)X_scaler = StandardScaler()x = X_scaler.fit_transform(x)# PCApca = PCA(n_components=0.9)# 保证降维后的数据保持90%的信息pca.fit(x)pca.transform(x
所以在实际使用PCA时,我们不需要选择k,而是直接设置n_components为float数据。
总结
PCA主成分数量k的选择,是一个数据压缩的问题。通常我们直接将sklearn中PCA方法参数n_components设置为float数据,来间接解决k值选取问题。
但有的时候我们降维只是为了观测数据(visualization),这种情况下一般将k选择为2或3。
参考
- Andrew NG在coursera的机器学习课程
- PCA的完整实现过程代码详解
- http://stackoverflow.com/questions/33509074/sklearn-pca-calculate-of-variance-retained-for-choosing-k
PCA误差的更多相关文章
- Stanford机器学习笔记-10. 降维(Dimensionality Reduction)
10. Dimensionality Reduction Content 10. Dimensionality Reduction 10.1 Motivation 10.1.1 Motivation ...
- PCA算法的最小平方误差解释
PCA算法另外一种理解角度是:最小化点到投影后点的距离平方和. 假设我们有m个样本点,且都位于n维空间 中,而我们要把原n维空间中的样本点投影到k维子空间W中去(k<n),并使得这m个点到投影点 ...
- 机器学习基础与实践(三)----数据降维之PCA
写在前面:本来这篇应该是上周四更新,但是上周四写了一篇深度学习的反向传播法的过程,就推迟更新了.本来想参考PRML来写,但是发现里面涉及到比较多的数学知识,写出来可能不好理解,我决定还是用最通俗的方法 ...
- PRML读书会第十二章 Continuous Latent Variables(PCA,Principal Component Analysis,PPCA,核PCA,Autoencoder,非线性流形)
主讲人 戴玮 (新浪微博: @戴玮_CASIA) Wilbur_中博(1954123) 20:00:49 我今天讲PRML的第十二章,连续隐变量.既然有连续隐变量,一定也有离散隐变量,那么离散隐变量是 ...
- PCA 主成分分析(Principal components analysis )
问题 1. 比如拿到一个汽车的样本,里面既有以“千米/每小时”度量的最大速度特征,也有“英里/小时”的最大速度特征,显然这两个特征有一个多余. 2. 拿到一个数学系的本科生期末考试成绩单,里面有三列, ...
- 机器学习公开课笔记(8):k-means聚类和PCA降维
K-Means算法 非监督式学习对一组无标签的数据试图发现其内在的结构,主要用途包括: 市场划分(Market Segmentation) 社交网络分析(Social Network Analysis ...
- 主元分析PCA理论分析及应用
首先,必须说明的是,这篇文章是完完全全复制百度文库当中的一篇文章.本人之前对PCA比较好奇,在看到这篇文章之后发现其对PCA的描述非常详细,因此迫不及待要跟大家分享一下,希望同样对PCA比较困惑的朋友 ...
- 四大机器学习降维算法:PCA、LDA、LLE、Laplacian Eigenmaps
四大机器学习降维算法:PCA.LDA.LLE.Laplacian Eigenmaps 机器学习领域中所谓的降维就是指采用某种映射方法,将原高维空间中的数据点映射到低维度的空间中.降维的本质是学习一个映 ...
- (六)6.6 Neurons Networks PCA
主成分分析(PCA)是一种经典的降维算法,基于基变换,数据原来位于标准坐标基下,将其投影到前k个最大特征值对应的特征向量所组成的基上,使得数据在新基各个维度有最大的方差,且在新基的各个维度上数据是不相 ...
随机推荐
- CentOS 7.2安装11g Grid Infrastructure
Preface Oracle claimed that 11g RAC is supported on Redhat Linux 7 and above version,but the ...
- linux部署maven
1.下载安装包 https://maven.apache.org/download.cgi 2.解压,并配置环境变量 vim /etc/profile export MAVEN_HOME=maven目 ...
- 前端开发工程师 - 02.JavaScript程序设计 - 期末考试
期末考试客观题 期末考试主观题 https://www.15yan.com/story/aY0HWAQ7oNU/ 1(8分) 函数myType用于根据输入参数返回相应的类型信息. 语法如下: ...
- Java开发工程师(Web方向) - 02.Servlet技术 - 第1章.Servlet
第1章--Servlet Servlet简介 Servlet应用于? 浏览器发出HTTP请求,服务器接收请求后返回响应给浏览器. 接收请求后到返回响应之间: 服务器将请求对象转交给Servlet容器 ...
- Python2快速入门教程,只需要这十五张图片就够了!
今天给大家分享的教程是适用于Python 2.7,但它可能适用于Python 2.Python 2.7将停止在2020中的支持. 与Python 2.7和3兼容的Python代码是完全可能的.通过使用 ...
- Anyproxy抓包工具
1.安装Nodejs和AnyProxy以及安装模拟器(移动端抓包工具) 第一步:nodejs下载地址:http://nodejs.cn/download/ 下载Windows版本,直接运行安装即可, ...
- visionpro9.0破解
visionpro9.0软件下载 提供一个visionpro9.0视频教程学习网站:点击下面链接进入. ------------------------Halcon,Visionpro高清视频教程,点 ...
- Django基本目录详解
1.app是自己建立的一个存放app的文件夹,因为项目大了之后会存在很多app(pycharm生成app方法 Tools-Run manage.py Task-输入startapp app名称) 2. ...
- SGU 194 Reactor Cooling(无源无汇上下界可行流)
Description The terrorist group leaded by a well known international terrorist Ben Bladen is bulidin ...
- Python—文件
def fileCopy(src, dst, srcEncoding, dstEncoding): with open(src, 'r', encoding=srcEncoding) as srcfp ...