BZOJ1509 & 洛谷4408：[NOI2003]逃学的小孩——题解

https://www.lydsy.com/JudgeOnline/problem.php?id=1509

https://www.luogu.org/problemnew/show/P4408

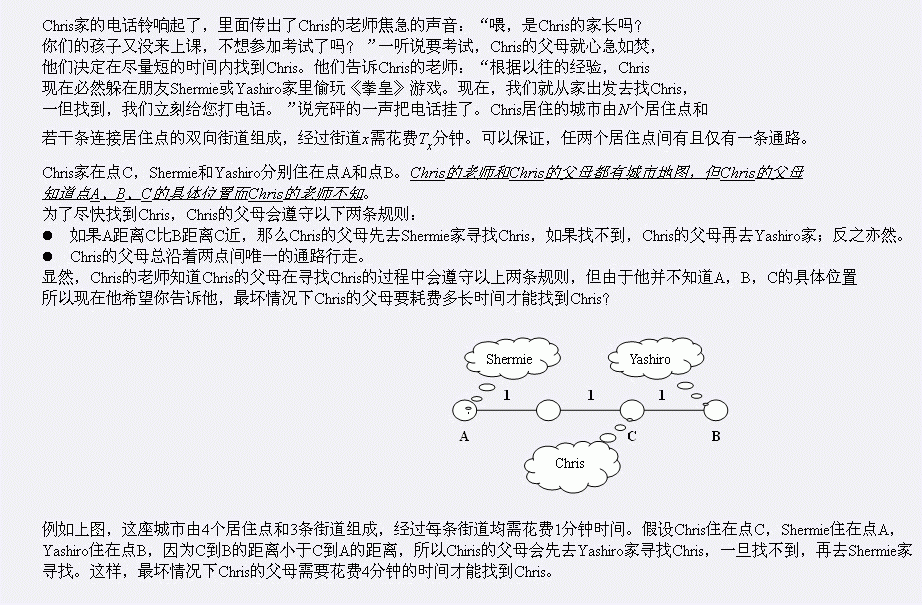
sb题，但是我至今不知道为什么这张图就一定是棵树……这题意没说明白啊……

显然求直径，再求一点使得该点到直径两端的点的距离的最小值最大。

没有什么好方法，最后一个点只能暴力，所以我们预处理两端点到每个点的dis即可。

于是我们两遍bfs求直径，顺道就给做了就行。

（然后我不会bfs求直径，我只会dp求……）

#include<cmath>
#include<stack>
#include<queue>
#include<cstdio>
#include<cctype>
#include<vector>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll INF=1e18;
const int N=2e5+;
inline int read(){
    int X=,w=;char ch=;
    while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
    while(isdigit(ch))X=(X<<)+(X<<)+(ch^),ch=getchar();
    return w?-X:X;
}
struct node{
    int to,nxt,w;
}e[N*];
int n,m,cnt,head[N];
ll dis[][N];
bool vis[N];
queue<int>q;
inline void add(int u,int v,int w){
    e[++cnt].to=v;e[cnt].w=w;e[cnt].nxt=head[u];head[u]=cnt;
}
int bfs(int s,int on){
    for(int i=;i<=n;i++)dis[on][i]=INF;
    dis[on][s]=;vis[s]=;q.push(s);
    while(!q.empty()){
    int u=q.front();q.pop();
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to,w=e[i].w;
        if(dis[on][v]>dis[on][u]+w){
        dis[on][v]=dis[on][u]+w;
        if(vis[v])continue;
        vis[v]=;q.push(v);
        }
    }
    vis[u]=;
    }
    ll maxn=;int id;
    for(int i=;i<=n;i++){
    if(maxn<dis[on][i]){
        maxn=dis[on][i];id=i;
    }
    }
    return id;
}
int main(){
    n=read(),m=read();
    for(int i=;i<=m;i++){
    int u=read(),v=read(),w=read();
    add(u,v,w);add(v,u,w);
    }
    int a,b;
    a=bfs(,);b=bfs(a,);bfs(b,);
    ll ans=;
    for(int i=;i<=n;i++){
    ans=max(ans,min(dis[][i],dis[][i]));
    }
    printf("%lld\n",ans+dis[][b]);
    return ;
}

+++++++++++++++++++++++++++++++++++++++++++

+本文作者：luyouqi233。 　　　　　　　　　　　　　　+

+欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/+

+++++++++++++++++++++++++++++++++++++++++++