zoj 3537 Cake(区间dp)

这道题目是经典的凸包的最优三角剖分，不过这个题目给的可能不是凸包，所以要提前判定一下是否为凸包，如果是凸包的话才能继续剖分，dp[i][j]表示已经排好序的凸包上的点ｉ－>ｊ上被分割成一个个小三角形的最小费用，那么dp[i][j] = min(dp[i][k]+dp[k][j]+cost[i][k]+cost[k][j]),其中，(j >= i+ 3,i+1<=k<=j-1,cost[i][k]为连一条i到k的线的费用)。

上一个图，来自博客http://blog.csdn.net/woshi250hua/article/details/7824433

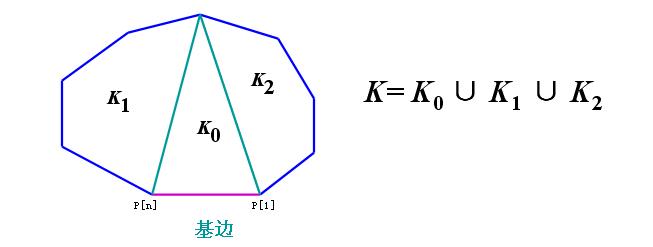
代码如下：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#define eps 1e-8
using namespace std;
typedef long long ll;
const int maxn = ;
const int inf = ( << );
int dp[maxn][maxn];
int cost[maxn][maxn];
struct point {
    int x, y;
};
point  p[maxn], convex[maxn];
bool cmp(const point &p1, const point &p2)
{
    return ((p1.y == p2.y && p1.x < p2.x) || p1.y < p2.y);
}
int x_multi(const point &p1, const point &p2, const point &p3)
{
    return ((p3.x - p1.x) * (p2.y - p1.y) - (p2.x - p1.x) * (p3.y - p1.y));
}
 
int sgn(double x)
{
    if (fabs(x) < eps)
        return ;
    return x >  ?  : -;
}
void convex_hull(point *p, point *convex, int n, int &len)//求凸包
{
    sort(p, p + n, cmp);
    int top = ;
    convex[] = p[];
    convex[] = p[];
    for (int i = ; i < n; i++)
    {
        while (top >  && x_multi(convex[top - ], convex[top], p[i]) <= )
            top--;
        convex[++top] = p[i];
    }
    int tmp = top;
    for (int i = n - ; i >= ; i--)
    {
        while (top > tmp && x_multi(convex[top - ], convex[top], p[i]) <= )
            top--;
        convex[++top] = p[i];
    }
    len = top;
}
int get_cost(const point &p1, const point &p2, const int &mod)
{
    return (abs(p1.x + p2.x) * abs(p1.y + p2.y)) % mod;
}
int main()
{
    int n, mod;
    while (~scanf("%d %d", &n, &mod))
    {
        for (int i = ; i < n; i++)
            scanf("%d %d", &p[i].x, &p[i].y);
        int len;
        convex_hull(p, convex, n, len);
        if (len < n)//如果不是凸包的话，
            puts("I can't cut.");
        else
        {
            memset(cost, , sizeof(cost));
            for (int i = ; i < n; i++)
                for (int j = i + ; j < n; j++)
                    cost[i][j] = cost[j][i] = get_cost(convex[i], convex[j], mod);//计算处各对角的费用
            for (int i = ; i < n; i++)//初始化dp
            {
                for (int j = ; j < n; j++)
                    dp[i][j] = inf;
                dp[i][i + ] = ;
            }
            for (int i = n - ; i >= ; i--)//必须逆序，因为dp[i][j] 是由dp[i][k], dp[k][j]推来的，而k是大于ｉ的，
                for (int j = i + ; j < n; j++)//同理顺序，因为ｋ小于ｊ
                    for (int k = i + ; k <= j - ; k++)
                        dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + cost[i][k] + cost[k][j]);
            printf("%d\n", dp[][n - ]);
        }
    }
    return ;
}