OpenCV(5)-图像掩码操作（卷积）-锐化

锐化概念

图像平滑过程是去除噪声的过程。图像的主要能量在低频部分，而噪声主要集中在高频部分。图像的边缘信息主要也在高频部分，在平滑处理后，将会丢不部分边缘信息。因此需要使用锐化技术来增强边缘。

平滑处理的本质是图像经过平均或积分运算，锐化进行逆运算（如微分）即可。微分运算是求信号变化频率，可以增强高频分量的作用。在对图像进行锐化处理前要确定图像有较高的信噪比，否则处理后的图像增加的噪声比信号多。

常用的微分运算有一阶微分和二阶微分。一阶微分

\[\frac{\partial f}{\partial x}=f(x+1)-f(x)
\]

二阶微分

\[\frac{\partial^2 f}{\partial x^2}=f(x+1)+f(x-1)-f(x)
\]

一阶微分特点：

1、平坦段为0

2、灰度阶梯和斜坡起始点为非0

3、斜坡面为非0

二阶微分特点：

1、平坦段为0

2、灰度阶梯和斜坡起始、终止处为非0

3、沿着常数斜率斜坡段为0

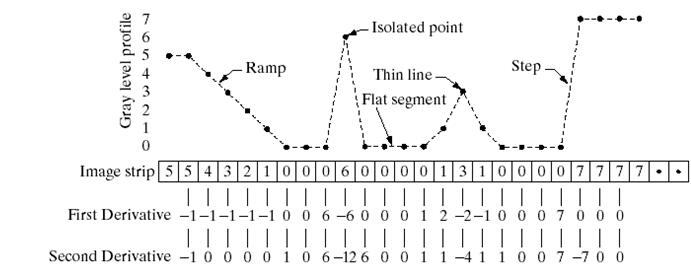
可以看出：

1、一阶微分能产生比较宽的边缘（沿斜坡很长一段为非0），而二阶微对细节更敏感（如细线、孤立点、斜坡起始点不为0）。

2、一阶微分都灰度阶跃反应强烈；二阶微分对灰度阶梯变换产生双相应（阶跃点两边都不为0）。

3、在大多数图像增强应用中，二阶微分效果好过一阶微分。

图像微分定义

图像数据是离散数据，用差分代替微分

x方向

\[\nabla_xf(x,y)=f(x+1,y)-f(x,y)
\]

y方向

\[\nabla_yf(x,y)=f(x,y+1)-f(x,y)
\]

其模和方向

\[|\nabla_{x,y}f(x,y)|=(\nabla_xf(x,y)^2+\nabla_yf(x,y)^2)^\frac{1}{2}
\]

\[\alpha = arctan\frac{\nabla_xf(x,y)}{\nabla_yf(x,y)}
\]

同理，可以得到二阶微分（差分公式）

x方向

\[\nabla_x^2f(x,y)=f(x+1,y)+f(x-1,y)-f(x,y)
\]

y方向

\[\nabla_y^2f(x,y)=f(x,y+1)+f(x,y-1)-f(x,y)
\]

其模和方向

\[|\nabla_{x,y}^2f(x,y)|=(\nabla_x^2f(x,y)^2+\nabla_y^2f(x,y)^2)^\frac{1}{2}
\]

\[\alpha = arctan\frac{\nabla_x^2f(x,y)}{\nabla_y^2f(x,y)}
\]

单方向一阶微分锐化

单方向一阶微分锐化是指锐化某一方向的边缘。最简单的就是锐化水平方向和垂直方向。

锐化水平方向

\[ \left[
\begin{matrix}
1 & 1 & 1 \\
0& 0 & 0 \\
-1 & -1 & -1
\end{matrix}
\right] \tag{3}
\]

锐化垂直方向

\[ \left[
\begin{matrix}
1 &0 & -1 \\
1& 0 & -1 \\
1 & 0 & -1
\end{matrix}
\right] \tag{3}
\]

锐化后可能出现像素值为负，这处理方法有：

(1):所有像素值统一加上一个值。这样处理效果类似浮雕。

(2):所有像素取绝对值，这样可以有效提取边缘。

实验：

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

int main(int argc, char* argv[]){
	const char* path = "";
	Mat img = imread(path);
	if (img.empty())
	{
		cout << "error";
		return -1;
	}
	imshow("原图像", img);

	//水平方向边缘提取
	Mat h_kern = (Mat_<float>(3, 3) << 1, 1, 1,
									0, 0, 0,
									-1, -1, -1);
	Mat h_mat;
	filter2D(img, h_mat, img.depth(), h_kern);
	imshow("水平方向边缘提取", h_mat);

	Mat v_kern = (Mat_<float>(3, 3) << 1, 0, -1,
									1, 0, -1,
									1, 0, -1);
	Mat v_mat;
	filter2D(img, v_mat, img.depth(), v_kern);
	imshow("线性非均值滤波2", v_mat);

	waitKey();
	return 0;

}

无方向一阶微分锐化

对于有规则的物体，单方向锐化有比较好的效果，但是对于不规则物体，常常需要无方向一节锐化。

交叉微分（Roberts算法）

\[g(x,y)=|f(x+1,y+1)-f(x,y)|+|f(x+1,y)-f(x,y+1)|
\]

\[\nabla_xf(x,y)=\left[
\begin{matrix}
-1 & 0 \\
0 & 1
\end{matrix}
\right] \tag{3}
\]

\[\nabla_yf(x,y)=\left[
\begin{matrix}
0 & 1 \\
-1 & 0
\end{matrix}
\right] \tag{3}
\]

Sobel锐化

\[g(x,y)=\{|\nabla_xf(x,y)|^2+|\nabla_yf(x,y)|^2\}^\frac{1}{2}
\]

\[\nabla_xf(x,y)=\left[
\begin{matrix}
-1 & -2 & -1 \\
0 & 0 & 0\\
1& 2 & 1
\end{matrix}
\right] \tag{3}
\]

\[\nabla_yf(x,y)=\left[
\begin{matrix}
-1 & 0 & 1 \\
-2 & 0 & 2\\
-1& 0 & 1
\end{matrix}
\right] \tag{3}
\]

OpenCV函数

void Sobel(InputArray src, OutputArray dst, int ddepth, int dx, int dy, int ksize=3, double scale=1, double delta=0, int borderType=BORDER_DEFAULT )

Priwitt锐化

\[g(x,y)=\{|\nabla_xf(x,y)|^2+|\nabla_yf(x,y)|^2\}^\frac{1}{2}
\]

\[\nabla_xf(x,y)=\left[
\begin{matrix}
-1 & -1 & -1 \\
0 & 0 & 0\\
1& 1 & 1
\end{matrix}
\right] \tag{3}
\]

\[\nabla_yf(x,y)=\left[
\begin{matrix}
-1 & 0 & 1 \\
-1 & 0 & 1\\
-1& 0 & 1
\end{matrix}
\right] \tag{3}
\]

实验

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;
int main(int argc, char* argv[]){
	const char* path = "";
	Mat img = imread(path);
	if (img.empty())
	{
		cout << "error";
		return -1;
	}
	imshow("原图像", img);

	/****************************Roberts**************************/
	Mat Roberts_kern_x = (Mat_<float>(2, 2) << -1, 0,
									0, 1);

	Mat Roberts_kern_y = (Mat_<float>(2, 2) << 0, 1,
											- 1, 0);

	Mat Roberts_Mat_x, Roberts_Mat_y, Roberts_Mat;

	filter2D(img, Roberts_Mat_x, img.depth(), Roberts_kern_x);
	filter2D(img, Roberts_Mat_y, img.depth(), Roberts_kern_y);
	Mat Roberts_abs_x, Roberts_abs_y;
	convertScaleAbs(Roberts_Mat_x, Roberts_abs_x);
	convertScaleAbs(Roberts_Mat_y, Roberts_abs_y);
	addWeighted(Roberts_abs_x, 0.5, Roberts_abs_y, 0.5, 0, Roberts_Mat);
	imshow("Roberts", Roberts_Mat);
	/****************************Roberts**************************/

	/****************************Sobel**************************/

	Mat Sobel_Mat_x, Sobel_Mat_y, Sobel_Mat;
	Sobel(img, Sobel_Mat_x, img.depth(), 1, 0);
	Sobel(img, Sobel_Mat_y, img.depth(), 0, 1);
	convertScaleAbs(Sobel_Mat_x, Sobel_Mat_x);
	convertScaleAbs(Sobel_Mat_y, Sobel_Mat_y);
	addWeighted(Sobel_Mat_x, 0.5, Sobel_Mat_y, 0.5, 0,  Sobel_Mat);
	imshow("Sobel", Sobel_Mat);

	/****************************Sobel**************************/

	/****************************Priwitt**************************/
	Mat Priwitt_kern_x = (Mat_<float>(3, 3) << -1, -1, -1, 0, 0, 0, 1, 1, 1);
	Mat Priwitt_kern_y = (Mat_<float>(3, 3) << -1, 0, 1, -1, 0, 1, -1, 0, 1);

	Mat Priwitt_Mat_x, Priwitt_Mat_y, Priwitt_Mat;
	filter2D(img, Priwitt_Mat_x, img.depth(), Priwitt_kern_x);
	filter2D(img, Priwitt_Mat_y, img.depth(), Priwitt_kern_y);
	convertScaleAbs(Priwitt_Mat_x, Priwitt_Mat_x);
	convertScaleAbs(Priwitt_Mat_y, Priwitt_Mat_y);
	addWeighted(Priwitt_Mat_x, 0.5, Priwitt_Mat_y, 0.5, 0, Priwitt_Mat);
	imshow("Peiwitt", Priwitt_Mat);

	waitKey();
	return 0;

}

结论：

Roberts算法的模板为2 * 2，提取边缘能力较弱。

Sobel算法与Priwitt算法的模板大小相同，属于同一类型，因此处理效果基本相同。

二阶微分锐化

有些灰度特性，一阶微分并不能有效提取，这时需要二阶微分

\[\frac{\partial^2 f_x(x,y)}{\partial x^2}=\partial f_x(x+1)-\partial f_x(x)=[f(x,y) - f(x-1,y)]-[f(x+1,y)-f(x,y)]
\]

\[\frac{\partial^2 f_y(x,y)}{\partial x^2}=\partial f_y(x+1)-\partial f_y(x)=[f(x,y) - f(x,y -1)]-[f(x,y + 1)-f(x,y)]
\]

\[\frac{\partial^2 f(x,y)}{\partial x^2}=4f(x,y) - f(x+1,y) - f(x-1,y)- f(x,y+1）-f(x,y-1)
\]

对应矩阵

\[H_1=\left[
\begin{matrix}
0 & -1 & 0 \\
-1 & 4 & -1\\
0& -1 &0
\end{matrix}
\right] \tag{3}
\]

上面矩阵即为Laplacian算子。Laplacian算子还有变形

Laplacian算子

\[H_2=\left[
\begin{matrix}
-1 & -1 & -1 \\
-1 & 8 & -1\\
-1& -1 & -1
\end{matrix}
\right] \tag{3}
\]

\[H_3=\left[
\begin{matrix}
1 & -2 & 1 \\
-2 & 4 & -2\\
1& -2 & 1
\end{matrix}
\right] \tag{3}
\]

\[H_4=\left[
\begin{matrix}
0 & -1 & 0 \\
-1 & 5 & -1\\
0& -1 & 0
\end{matrix}
\right] \tag{3}
\]

上面几个算子，\(H_1\)和\(H_2\)效果接近，\(H_3\)效果比较差，\(H_4\)相加后为1，接近原图。

Wallis算子

在处理时，加入对数处理过程。

\[g(x,y)=log[f(x,y)] -\frac{1}{4}[logf(x-1,y) + logf(x+1，y)+logf(x,y-1)+logf(x,y-1)]
\]

在前面的算法公式中注意以下几点：

1）为了防止对0取对数，计算时实际上是用log(f(i, j) + 1);

2）因为对数值很小log(256) = 5.45, 所以计算

时用46*log(f(i, j) + 1)。

（46 = 255 / log(256)）

高斯-拉普拉斯算子

Laplacian算子对噪声很敏感，所以在进行锐化之前，需要先对图像进行平滑，减小噪声影响。高斯拉普拉斯算子将平滑和锐化结合在一起，适应了上面的需求。