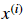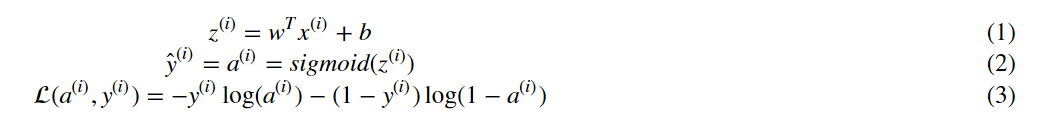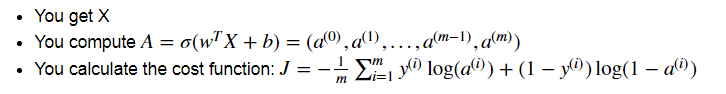Logistic Regression with a Neural Network mindset
You will learn to:
- Build the general architecture of a learning algorithm, including:
- Initializing parameters(初始化参数)
- Calculating the cost function and its gradient(计算代价函数,和他的梯度)
- Using an optimization algorithm (gradient descent)(使用梯度下降优化算法)
- Gather all three functions above into a main model function, in the right order.
1 - Packages(导入包,加载数据集)
其中,用到的Python包有:
- numpy 是使用Python进行科学计算的基础包。
- h5py Python提供读取HDF5二进制数据格式文件的接口,本次的训练及测试图片集是以HDF5储存的。
- matplotlib 是Python中著名的绘图库。
- PIL (Python Image Library) 为 Python提供图像处理功能。
- scipy 基于NumPy来做高等数学、信号处理、优化、统计和许多其它科学任务的拓展库。
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset # 用来导入数据集的
%matplotlib inline #设置matplotlib在行内显示图片
%load lr_utils.py, 如果该作业在本地运行,该代码保存在 lr_utils.py文件,和当前项目保存在一个文件夹下
import numpy as np
import h5py
def load_dataset():
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
2 - Overview of the Problem set(目标:预处理数据)
Problem Statement: You are given a dataset ("data.h5") containing:
- a training set of m_train images labeled as cat (y=1) or non-cat (y=0)
- a test set of m_test images labeled as cat or non-cat
- each image is of shape (num_px, num_px, 3) where 3 is for the 3 channels (RGB). Thus, each image is square (height = num_px) and (width = num_px).
2.1 导入数据
# Loading the data (cat/non-cat)
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
2.2 熟悉数据
我们打算预处理这些数据,重新命名数据为 train_set_x, test_set_x。标签数据没必要预处理
train_set_x 和 test_set_x 是一个数组,代表一个图像,你可以运行下面代码预览一个例子,也可以通过修改索引查看其它图片)
# Example of a picture
index = 25
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:,index]) + ", it's a '" + classes[np.squeeze(train_set_y[:,index])].decode("utf-8") + "' picture.")
y = [1], it's a 'cat' picture.
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWAAAAFdCAYAAAA9hbc/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz%0AAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBo%0AdHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJztvWmwZdlV3/lfZ7rDu2/KOVNVkkpo%0AaDQQchRqgwIkbFMMHRgj9wfUmLEJcIiANuAIcKkJo/4gy0EALltIwAfCxjY0xjYNSA41JeEWjZFM%0ASEKyJJCFUJeqKpWVWZXTm+5wpt0f3s2qu9f6Z+V7WZl1blauX8SLzLPvPufus/c++523/nutJSEE%0AOI7jOM8/SdcNcBzHuVvxBdhxHKcjfAF2HMfpCF+AHcdxOsIXYMdxnI7wBdhxHKcjfAF2HMfpCF+A%0AHcdxOsIXYMdxnI7wBdhxHKcjbtsCLCI/IiKPiMhURD4hIl9/u77LcRznTiS7HRcVke8E8BCAHwHw%0AJwD+PoAPiMirQwiP3eBcAXAGwM7taJvjOM5tYhXAuXCIADtyO4LxiMifAvizEMLbFso+B+B3QwgP%0A3uDcFwE4e8sb5TiOc/u5J4Tw5YNWvuVvwCJSALgfwD9VHz0M4I0HuMQOAPzod38tesUzzUtE1PdY%0A64moOgCQkjJ9LYTW1Nnempmyz3/pYnT8549cNXW29ipT9vLThSl74+t70fGZk3YoBsPUlCGNf2GK%0A2LanYn+psr6RRh1ntp394SZp18iUFf1+fK3E3k/T1qasbeP2BzIWAOkHUq1tgjq299wEMh+UJS6A%0A9BU5j9ULrZ5bpJ2tLWzU/YTW3mBD7iew+0ni6zM7Ywi2tKnisrphjWfPna2m51uSkD4lDSOXgn5H%0AZPcMcj+6XlM3ps50MrZlU1t2dWsSHX/psfjZr5oG7/uzzwGH/Mv9dpggjmH/ibmgyi8AOKUri0gP%0AwOJqtAoAvSK7JQtwdpML8Kywg5Vn8UKQJKwNtixNbVkvj8v6PbvIDEiZWYDJJL75BZi0oU9+MQxy%0AU1b047KELMC1XpxwFyzArJ0HWIB1vwDPwwKs5mldP5cFOK6XpB0swGosmtQ+09LaFya0dn738rie%0AXgtultu5C0KPnpAyAHgQwNbCj5sfHMe5K7gdC/BFAA3s2+4J2LdiAHgXgPWFn3tuQ5scx3GWjltu%0AggghlCLyCQAPAPi/Fj56AMDvkfozAE8bXK/9qZykEv3Zkui/V8i7tJA/Q8hfchD1J3pK/jwa9O2f%0AIRursY10bWC7b3vP2jkvb9uynZ34WvUxe0PGVAJiS2N//pHOEfK3sLHENNbuXc52TVme2/vOsrjv%0AM2I+KQp7njY5MBME1YmJOaPRf3JW9sRA/qxuVFlLrs1MCcx01SjzAmt7sH8Jw1glyPexv7zJ1CXm%0AJnY/7M/4G9uvGdwMcqM28fnN0OYfavoh75KiGhGIHTrLeqasN7DX2pDV6Pil7UZ0PKsq4GOfNefd%0AiNuyDQ3ALwL4NyLycQAfBfDDAF4M4Fdu0/c5juPccdyWBTiE8O9E5CiAfwzgNIDPAvifQgiP3o7v%0AcxzHuRO5XW/ACCG8F8B7b9f1Hcdx7nRu2wL8XBGEyJYpypjGtgUxg5vQjS0Ksi0oJ1vMVtVe16Mr%0A1k58Zcdua9mbWhvw1k5sCGzIbpiE3GMqse04HNCOhmDboE9ltuO2tnsiZxN732ka23xF7NRKe3af%0AsR4eukWL7kdlW7KU3VmsHZpt0QuqjJk+G2abZlvFtA2YtZPYgPXUZaPK99KSMm3KDcT2zmzM5vmh%0Am8LI9924DXzbKLkWeYb1lrlA5gibuzB9w+zQZEslsQuno7hMT61pWdrvPwAejMdxHKcjfAF2HMfp%0ACF+AHcdxOsIXYMdxnI5YWhEObRL7nSuDut5kDVif/v2yGwtz1FeeFI4GsSH+6NrQ1Hlya2rKLpLw%0AHONprILUxM+fioq6SAtPAJCQ8xIrNhjxkapDtqiaWWFuDCUOtlbIKEhMBx0yQjtTAEBNHCpa4lDR%0ANkpoZIN4gDgCTOBNSUc0RFjS8435b7Dx0Vei85udx3wsVPuZM1JD5paeDlxcO2BMB9VWScjcYiIf%0AdVxRzjrkhmi79MXIPSdEcBPpm7JM4npJHs/ldGadmA6CvwE7juN0hC/AjuM4HeELsOM4Tkf4Auw4%0AjtMRSyvChbkv3DVEuZ6kRH1ImacLC66ti2gQcMtQBSI/cWTF1Dl/yUYP25kQLzRTwsK7EbFBCQks%0AohSNHsY85pRQEljAbyJ4sLKyjTMGgIhwoSUR0oYqkDsJXs+i1THvRZ3xoKltv3OdUXnx0RBzBxB5%0AYIPvk9tBIOfp4P4J8eJjQ0i6wUR8O2g0OS1kMe81E5UQoPNUq8X0EWNCIPF6NOey4PjMw7GJB1sS%0A64mZpQNTlmSrtkyJ2D0lfqepFd8Pgr8BO47jdIQvwI7jOB3hC7DjOE5H+ALsOI7TEUsrwrVtE6eG%0AMZHliEhBPYVIGDx9TMSNjP1qGsTfub5qhaaja9bQf2XXGuh1W9OUtZ15/BhFwtYxJdy7q1V9IzpN%0AMq6TUoeFYVRhK0kG+usoRrGQWZCMy1lOhDkS2TJN4vGpSns/VcnCXcb1qGhFC1kanLhvWEZsHboT%0AsKEZ9XUAoGUptyqWaVqVMSc0pvlCz4eDeb1R7zU11m3L8jAxRZQ9r6pdRIBvG3IttUZkhfVclcwK%0A6WlGhDkVXlVnjBaSBfwg+Buw4zhOR/gC7DiO0xG+ADuO43TE0tqABUlk+9Fmx5bEmWLpeQKxa+oN%0A5ixiGnNw6Pfi81ZG1pZ3dNNGUnryqnXOOEjmcBb9ytq5D5qGidzjQVLQkF/RbUPsk7WK7oZt2wJi%0A8wvKWNw21k7XG5IN9CTFfZHH7c8y4vhR2LbXqu1tRWzcNI0QszvGh2lm29lObeQsbb+WPnFkIU4K%0AzNbeVHG7WmL3Di1xstCp5A+4OrA0Uq1ygmHtpNoLcbrRNnOqSxCNI0niPswyEuWsR9IPkXr6HrUz%0ATUrm2kHwN2DHcZyO8AXYcRynI3wBdhzH6QhfgB3HcTpiaUW4NJE44pkysgcSzYnt62am8STVUZ9I%0AHbLZO0vj7hr2rDh0fHNkyi6QnERZWqk2EGWBpHGRVEV4IkoJc7rQG+MBIFDnghuTEEcC7UcSSCSy%0AurRi5LiN+6GuJ6ZOXdnN8oOh3Sxf9GMnjjwnQt3AluluaGviwEFSINU6BRJs39ckVc3FR54wZStr%0AG/HxsQ1Tp65MEaqZHeumjNtVz0hUODL2mUrPk/asGBWIJ0ZVkrFWfZiS89j4MCcVLaa2DXHWyIln%0AjsRzJE3s/RQ9O7cks9eqlfAsiO9ZqOfWjfE3YMdxnI7wBdhxHKcjfAF2HMfpCF+AHcdxOmJpRbgk%0ACUgXvb6UuCE0VQ7zhGMKmxaybJWMRLHKlaG937eRu9ZJNLTjm9a7a1ZvRccsUBh1TFNqV0I8AilE%0AVExUCiKdygbgkc9IUTxWANKciENEJW2aWJgrJzZyXFNb8a6p1kxZv4wFlf7QejkVAzs+ufJWk74d%0A+4ylQGrs41MrQerKo1dMnZW1l5my0MQKW7m9Z69dkf4jwlxbKs8+EhWOjWudxX0fiOrXkqhfZU2i%0A9hlPMfuspMQbT1ryner6IlaAzUkEsxDiMmHef0SmDzSNmSozrrkHfA7N9zuO4zid4Auw4zhOR/gC%0A7DiO0xFLawMWCZFzQqZsnwd1NqDh+pWNR6cEB4CMbKxWAavQ79k2jFasjfHYEWufeupKHC2sIW3X%0AKej326o2uCd2E3wSmF3L2uCqaXz9esfa39JV2w+B2Ol0S5PsYBHmMpUBgWU2aIN1ziinbPP/VB3b%0ATfb9yo5FT9nyM+Jgw6JdZWTejHdix4sEJ02dfOWlpmx2+Wx03GxfMnV0hLH9QlskymaaEtsxS//e%0AqGeqmZX24oW1q7Owadrvgs2ZurVOKmjtPNXZJgK56bywDlCiH1jiwNHMSAfS0G3xYaI0In18UPwN%0A2HEcpyN8AXYcx+kIX4Adx3E64tALsIi8SUTeJyLnRCSIyHeoz0VE3jH/fCIiHxaR19y6JjuO47ww%0AuBkRbgXAfwPwLwH8R/L5TwH4SQDfD+AvAfwMgA+KyKtCCDYs2HUIaCNju6hIZDnznmCptpm4pU7V%0AG/EBblTXm7FTEs2pP7BG/Y01K1zsTmKhp66tIBFIiu7MpLO338fELp1CBQCmZXz9EGwELqmsIJEW%0A1kmgDWqzPEunpEOmARAlZOkU5MB1It8xpxsl9MxK284Q7P20TRwlKycOKToS3v732b6fXImv31t7%0AqT2vtNdqtrXQaB1ShIhPJIMP9JQIpE8bch50Wqm9sT1vZsU0Fj0M2hGHPE9VY4XNurTCn9aiQ2tF%0A2d7AinCDoXLWYc40YyI09oiIrYu0Y9NNRhY89AIcQvgAgA8AdkGS/YIfB/DOEMLvzMu+D8AFAN8F%0A4FdvqpWO4zgvQG61Dfg+AKcAPHytIIQwA/BHAN7IThCRnoisXfsBsHqL2+Q4jrOU3OoF+NT83wuq%0A/MLCZ5oHAWwt/Jy9Tj3HcZwXFLdrFwTLd349I8m7AKwv/Nxzm9rkOI6zVNxqT7jz839PAVjMu3IC%0A9q0YwNMmiqcVqKftyk3Y/5nTiopgRgQw5r2GYL2AciUI5MSjjWRGsd4wROzqky5dW7Ei3KqK1LXf%0ADTEsKpNOp5QcUIRjSIijtK1uvsTUaUkksjo8Zr9zRfczyQ9F0i7p1E8ituNZWWhtP2thjjjVUeGs%0AnMZ938yICEeiZpVEpEqSM/F5PWtRC3u2T3tK+CO3R9NWmShdAHTQL6HziPSzekcKFfF4rIj3Gulo%0A0aoVeV7b2gpgJflOHWGuIR5tozWbbqhXxKJyoj3jAMwm9n6EeEJCrRFBjUU1taLpQbjVb8CPYH8R%0AfuBagYgUAN4M4CO3+Lscx3HuaA79BiwiIwAvXyi6T0ReD+ByCOExEXkIwNtF5AsAvgDg7QDGAH7z%0AVjTYcRznhcLNmCC+GsD/s3D8i/N/fx37e39/DsAAwHsBbAL4UwDfdJg9wI7jOHcDN7MP+MOguRqe%0A/jwAeMf8x3Ecx7kOSxuOcjaZRcb9TIVdFJJaJu2zdDPW8N7rx2VpQbzeiOiixa1Ex9wD90waDmw3%0Aj0ZKmCMnMvEkVaJVwjzOhKhPJOqeFpuawp43WLfhFMdbVnAo8jh8ouTW40yLPIANLShkSgrsuLZk%0AfESJcMxbrpnae6yUN1Q5s+JaWdm2tyQlUbF+RF3c9kNOwh22WtShXoM3FjH3K8aHgXhp8RRYSsQk%0ASmBgoRqJ0C063VWw4tqstPOomllRTKckaogb3zicN2XDUbzzNemTtEVEQGym1tOureI26Gi4rN0H%0AwYPxOI7jdIQvwI7jOB3hC7DjOE5HLK0NuK5apAub+bW5tRJri5qRTemp2BQnQe1UZ+nYyd5/sumd%0ApOMm5+mUNwCwNoo3jlcsFYuQ62vHhYSlwyap5En+8mYS2z7bnKSEH9oN7kW+acqCckron2Bpi4jt%0AU9kPSeZ6ZmIESKQ47b2QsPNYFLUqvu8ZSQlfkShg2Yp1XBGJbftC0ghVV22qep1+qmCOGJm9oSRj%0A2oGahOS5aEiKdpOFnvUxsSfXzBFDDWRDUiCRRxgZe4CUA0XDIo/Vdu62rSpjTktE/0Egz5T6Tn3P%0AgaWLOgD+Buw4jtMRvgA7juN0hC/AjuM4HeELsOM4TkcsrQjX72foLSgRWo9iG8IrEpBoxqJgKlWH%0ApSTKrfYEyWOhLCG/vpiLYJ5bYWGlH39nRTa9JwmJ1KQ7grWBiBRCopOluh7ZGB+IU0JGokVNr8b3%0A2K7a78tGRGBR1Rqif9QzW1jPiOihTk5ZQLaSiIM7qp/3bD9kmY1olw2sGNnfjCeO1Lav9iobBSzT%0AUe4S286EqIo6Oh4AiIr2l5CJGogjS6V0YBZ9jaXJAhkfOwVJG4iAyPS1oO+btMukQAIgagKkfeLk%0AQ0Q/5lQRaiV+6+vc5KusvwE7juN0hC/AjuM4HeELsOM4Tkf4Auw4jtMRSyvC5f0MxaI7UKPTpRCB%0AgCg4s6kVM1pVr2UpiUgUtVZ50rBoaCwbUEJSJfV7seKRNVbkEVixxlyblLFURkbFBJApMaPVYhSA%0AMrFhnNOTNkJaoQSp6UUSnYp4HbVKJG3ILZcT2/Zq14pwQaWuSWvioTUjytwsFt3ahly7d8yU9VZX%0ATFl/Ix7X2SX7fUzIkkzXIUIQ82bUqX8AJKmql5PIgWROFrny4iMeYWxusbKqjMdVaPg1EqWNRRhU%0AInbCUjMR1VzS+H6ygX3G0sx6oBJ90ng0hjK+55SFGzwA/gbsOI7TEb4AO47jdIQvwI7jOB2xtDZg%0AjWjbEI1WRmx+xCirN6azFN0stbv+bcXsvdQGTLIWFEVsl5PK2qcSkAhPyj7J7NCB2dtIUdZTWRi2%0ArAGWRYuqp9Y+mfXW4vNm1nY8vrBtz1uLr1+TjBXN1NrXmjHJQKBswDmLJkdMwKnaxF+xQUxHpqhN%0A7JiNr8R9GGZESyDeBukg/s6ytA1lEe2YQ1KCuG/SgpzXI5HBsrhdaWqXh16P3A9LwKILiWbDHIZA%0AbNqNsuUK0WfqYMeiruJ6gVw7H9osGWxtgXLO0E4kKY1KeGP8DdhxHKcjfAF2HMfpCF+AHcdxOsIX%0AYMdxnI5YWhEuNAlCs/j7QUUjIpuxmWiQkw3nWkjIyV5slgJc611MqGOiH0sRpB092tZuJA+w6bFr%0AlUqepd2hGVXI79p0qNLG2P36KPdsNLS0sqIO8vj6WWHvZ0acM0SJVAUR/YaZHYvsCIkep6ZzSsai%0AnNi2lypCWqht20vtKQGgJOnL0yIW65LMdmq2QiKrDePjKYkwJsTRiGWJb1S9pibzjzipJHmjjq1A%0AJYlVqAp7O2jVVxINjop3VUXSJ2XxeKTFmqlTl7YjppO4rCIR9IYpeS5I1LQ0xOe26iFjjlsHwd+A%0AHcdxOsIXYMdxnI7wBdhxHKcjfAF2HMfpiOUV4dpYTNLiFjN5pyTFSVEQ7xclzBGdjqc90VWIhxv1%0AoCPXT1QqlEBEuLq16sZMiUiBjCCTAYWkrlHaBuqeveeCeHvlA6taSqGuTxrWI6mM6u1L8bWHRADp%0A2e8brNn+mlxVgiGZJElBInCVsaBSkKhZiZAUWCR0W1vuRsfjK1dMnaJPvK8SdS3mWBXsGGqxC7Ai%0AbFvbe24aFhUuFhWzgqSV6pGIYqkd155+7loirpGoc6iJp10Si25ZbiPTobGC6GSqPD1JJLyaeBxm%0ATIRTnqtt4tHQHMdx7mh8AXYcx+kIX4Adx3E6whdgx3GcjlhaEU5CiMLVJSqeIkvzU2ghCDQbCzJ1%0A10wkYw5tQRnaA1FAAhG7mCqWKg+cQIaiLa3gUY5jkUeIO1Ge2y9MiWCYDpQ3T5+kbwLpQFjxpC3j%0A0JmhJKmMmCCq3wFIvMhqakWkCRE9yolKLUTCHdbEAyxTrlwNSRmUFyRXktiQmOPLF+Pv27XfN1g7%0AYcqK1Xj8wwX7dczrjc1BPd9oGiE2d/XwtyTkJxHvEhbaUqUIyoi7aUoEt6JlIpyag8mq/T7ijlfO%0A4jGrSBjVesLSfpEQrKWqpwVRomkeBH8DdhzH6QhfgB3HcTriUAuwiDwoIh8TkR0ReVJEfldEXqXq%0A9ETk3SJyUUT2ROT3ReSeW9tsx3GcO5/D2oDfDOA9AD42P/edAB4WkVeHEPbmdR4C8LcBvBXAJQC/%0AAOD9InJ/COHAlpK2DWgXUuukeWzPY9mkWVSzjDhnJKmOrGbP40HNVBp3mn7oxg4cgI0qpVMUAUDL%0AHDGUgwNLoa7T2wAADdakbKTFmp0OM7u/HdXuJVMWlCOBtMRJoSIX07a0yt5PObapmdLEOmJUVWyL%0AHK7YCcFS/WS9+L6ritnjSXSyfM+UTfbiPr36hD0vJ44La0fjd6GKREMDsV8z5wwdsIxF9mOmY10Y%0AWKQ1YuxkUfsSNbeECC3MLtwj74SVvhaJephpYQdAojWH1PYDtQuT+y6VxqEdWSbkOgfhUAtwCOFb%0AFo9F5AcAPAngfgD/r4isA/hBAN8TQvjQvM53A3gcwDcC+IObaqXjOM4LkOdqA16f/3t5/u/9AHIA%0AD1+rEEI4B+CzAN7ILjA3Waxd+wFgJU7HcZwXIDe9AMt+cIZfBPBfQgifnRefAlCGELQD/IX5Z4wH%0AAWwt/Jy92TY5juPcSTyXN+BfAvBVAP6XA9QV0MToAIB3Yf9N+tqPC3aO49wV3JQjhoi8G8C3A3hT%0ACGHxjfU8gEJENtVb8AkAH2HXCiHMADxtwb4W9SzJBMmCgJZnOo0QMeoTJ4iEGP91ZDUW1Yx5T+h9%0A/XQzO9nEz37PJakWFYnwAytSTCdxJK1AFINE504CwO4nVSlnkgGZDsSZYfvqlimr1Kb90RrZzF5Z%0AoSJRfd8jkagGxMGmIjlu0jTur8DSUbFIZ8opZrQyMnXK0l6rrawId2RDh5iz91MU1uGl2o4dbJqK%0ACG4ktZCQuaXnM4vQx9B6Hhl6qjxTsU7r7SSyWqIdLMCdiPpt3F9Z395zyOy4BonnQ5+kgmI9UxHR%0At9yNx7pSTh7T8uZEuMNuQxMR+SUAfxfA3wwhPKKqfAJABeCBhXNOA3gtrrMAO47j3K0c9g34PQC+%0AC8DfAbAjItfsulshhEkIYUtEfg3AL4jIJeyLcz8P4DMAPnSrGu04jvNC4LAL8Nvm/35Ylf8AgH81%0A//9PYD9YwG8DGAD4QwDff5g9wI7jOHcDh90HfENjUghhCuDH5j+O4zjOdVjaaGhFkaAonjFRa6cZ%0A4vhihC0AYHqUKNGF78+wv2uMeEfSFgm9GBFP1OXzHjPHW2+vXn89Oq7H1sVNGiJQFfZaRW8jvtbU%0ARjCb7tqUOoFEYOupdEYSdk2dlkTS6inBK0ltnfGu9bQaDuz9lHuxMNLfWLN1LlrhLCTxZBLiZjkg%0A4mA7sW1tZnFapKNHSJSuiRVsnvpyLGym5F0niB3rQJQyXUbFNIL2VmvJM6CjEl4rNW3QXnuJVeok%0AY0IqiWiIuL9Ca8ewR8YsqLYWxFOWhZhrJ1aEa7biOVhdjed3VbGoajfGg/E4juN0hC/AjuM4HeEL%0AsOM4Tkf4Auw4jtMRSyvCZWmLLHtGvNKiGwuvSL3eSCg+nVpImNjAUvgogSClbSDXYuEuVVMTEjYz%0AFxKur7cSX2dqxaiEbPhL6qEpSxGLcFVtRTgh4kmPhLuULPZWCo0VJVY2BqYsX1FlFUmLxNIUlSTd%0AkD6VhC1sdaxGAPlq3IezXSvyDE4cMWWTHRJqUntytVZArFor8uwo4WeNTPCEiJ8s7ZImBOKxCSLe%0AyrMfAzT6JRImMqtnqiWhNCVj7bJlqcRzqSkvmjpJnwjiWtAj4jQackPEw1HKiTqOJ5uQMKoHwd+A%0AHcdxOsIXYMdxnI7wBdhxHKcjltYGnCQpkgV7XarsuyzFiRwwCpgpI9dKiQ1OR2Bjm8aZPdk4fgBI%0A1Sb0lKVUIUbmTEWQKklUsKYkKVvERvhK12K7ZlWdM3V2SOSz/iqJ7qYMzz1t2wWQkyhjoqJYbV+1%0A9rfRpj1vmzlUiEotVNqxGK5ZW3h/FPfplLShmdl+nl61NvPeKLYns8h0o6G17Wcn4no1cfKo9qxd%0Anc0RHaSvbaxdtSUOFaKuxeYtixzIbMVtG5+rnSIAQFqizzBdRVp1bJ18kprYd1X6rnpsxwuBeGcQ%0A5wxJ474vVuKGNla6OBD+Buw4jtMRvgA7juN0hC/AjuM4HeELsOM4TkcsrQgnSQtJnjG+67QxB9fb%0AmGOEcqggqWsykgZH62S6TezaAECqIVMb9pmomLRkM75OedSQCFmtjcCVJTbZdDHYjI63rLaBC0/Z%0AwntI5LbBKP7OwjaBbsbvrcSiVSAb2nsDK5RIYqduUOGu9sYkJVFuhaxqEgs4JRHvVoJVWYabNqVO%0AMYhFPuMcAgBi7zGbxY4Y+Yq99pQ4iGhxev/6sWjVEIEqgKQIOkiqLpIKLBAxzZxJPDga4iBCPT2C%0AFuGsI4s0NsKcnm+zbRKxTOxEbRvb9zoynJ5rATenwvkbsOM4Tkf4Auw4jtMRvgA7juN0hC/AjuM4%0AHbG0IlySCNJFEUDb+YnhHywl0XWuvQiLrJYyjx8VWS0hkdZYRLaU1NMCB0vz0xK7fmjjIUvERkPL%0A+tYLrSCeaU0dp88J08dNnVMnmTeZvce8r7yoiDdRtTc2ZZLFwlJb22u3JGIVCwIm/VgAyzfPmDr1%0AzqO2XTM1AYR4y21umDKs2j5NlKfi5IoVjNpq25Rl/fi8UNlJ2dQHi9qX9OI50hKxq2VeaFpAZs8A%0AU5SJoBfUkycknRK7PhMHtYeriBXc2PMTmngO1hMrYlYlOS8hEQZzFYVQpUBqyXw/CP4G7DiO0xG+%0AADuO43SEL8CO4zgdsbQ2YIQQGfpaFeKpIb87aEp4lo2CWoZNA0iT4jLdpv1rExsmSV/fKNtTSzbL%0At8QhoFROAy1xxEiGK6YsJRG4mvJydFwkV+15I5Kpo8+yKSj7OHHE6KXWZhqUHbAmtsLdK9bmJ8Th%0Apb8ep6Ffv/deU+f8py+Zsukk3qCf5bb/zv6VtR8+ecE6qdx7Jm7DCun3moyrdizhtlb7uDaNtWEW%0AqfrOgszl2tosdbKQJCHzm8zlwNqqxifPSdQ28rjWxFmn1VkytDMS7LO5X6aO2XPPziPPtXZuCSo6%0AWkjdBuw4jnNH4Quw4zhOR/gC7DiO0xG+ADuO43TE0opwIYQo5Xaj0qoIMcS3THAjBvVWVWRCFkvZ%0AApVmheZiIZGuarIRvlQbzoUJHmR46joWWISIG/nQKmD50G4ur6fx/RQ9FjmOCB5EzGhVLpmksNHX%0A9sa2XeU4dkAYjqzDw3Rqxa6qsmLN5pFYANu455WmzuXHrAi3d/HJ6Pixx63o9/ufsqmZLlyywtwD%0A98Xj+NUvt/e8umr7rzdQUeHIZM4KG6WrnFjnlqAcV5LUnpeSuav1TzbOLLVQkpFodSrtPUudpNsJ%0AABKIY4RS61oWCY+JadoZRKuMABKSkYimKRIdClFfiKwXB8DfgB3HcTrCF2DHcZyO8AXYcRynI3wB%0AdhzH6YilFeHadv/nGtp7zXg63W24AAAgAElEQVTHAGgbIhAQ0UB74NQsMwoRDZIkFtgS1gbiYdQS%0Ab6VERW4rBiTCmM6BBCAfxoJKsW7Frv6q9eTKBlYMqivlvZbadpJbRFMx76F4fL78BdsPH/zkxJT9%0A90ux993rjtk2fMvfOGLKEpJaKO/H93jk5KtMnYtnrLffZEe16ewX7Xl7VpgrNk6ZsuOvUMLmEdvv%0AT561QuDmelyv17fCWV7Y+VCO7QBV07jvUzL2LOVWkDj8XksijLFof1nOlhEVHY/p1URwA+y8Cco7%0ArmGCNXlWWv2lJOxhRiKytUzg1+uI6Pu7uXdZfwN2HMfpCF+AHcdxOuJQC7CIvE1EPi0i2/Ofj4rI%0Aty583hORd4vIRRHZE5HfF5F7bn2zHcdx7nwO+wZ8FsA/AvDV85//DOD3ROQ1888fAvAWAG8F8HUA%0ARgDeLzQcvuM4zt3NoUS4EML7VNH/LiJvA/A1InIWwA8C+J4QwocAQES+G8DjAL4RwB8c5rvaJkSi%0AWqLC4DGvN5ZmhYW8E1XIws+xcH0izQ3rNDXJI0RC+PVHsbdNTrycen3rvZbmsadYb2AFqv7Kuikr%0AmCfcTIkzRClhKW9mu/a+Zyrdy6XSft+0sL/vH9uK++vVX2HTAV3ash5n997DwhvGQlmS2zYMVtZM%0AWR3ivi+Dvfa3fcPIlE3IWL/4JfF3njlOUkaFTVO2dT72aGPzIcuJR1tuvbZKFeq0V9jxKohoFdT7%0AWCAiWUJCT6ZMhFNeo+zZZA8nS+2jxcCEvM+xdpmrE2GdaWcJXQ/0WKs0Scxz9gDctA1YRFIReSuA%0AFQAfBXA/gBzAw9fqhBDOAfgsgDc+y3V6IrJ27QeAlfUdx3FegBx6ARaR14nILoAZgF8B8JYQwl8A%0AOAWgDCFcUadcmH92PR4EsLXwc/awbXIcx7kTuZk34M8DeD2ArwHwywB+XURe/Sz1BSy9xDO8C8D6%0Awo+Ldo7j3BUc2hEjhFAC+Kv54cdF5A0A/gGAfwegEJFN9RZ8AsBHnuV6M+y/TQN4JtVMaEMUBSno%0AaEPEQYAUoRHmZaHsN4215XFHj7he01pnAGIyRUGik/WUQ0VvxdoYB6Ojpiwfnlbn2T8u+kNr58yJ%0A/bCcKIcAsXWa0jpP7GxbO53e7H/slLXlftWadWbYU5v/v+q1tt+nW9Z2VwyJHbCI7aFpau2vvaG1%0Aj/eVbXptxVrBTm9Ye2ie2LLj6/F3TrZtWvrB0KZm2knifmZORXVtH9eEpFCv6/haTcnsr7ZIT16W%0AXotFx0uIdqB7RkczBHgqeZCURFqjkYykjS/sM9Zquy1ZCxpihyaSDUKI53ymnpWUnXQAbsU+YAHQ%0AA/AJABWAB57+QOQ0gNfiWRZgx3Gcu5VDvQGLyD8B8AHs72xYxf52s28A8C0hhC0R+TUAvyAilwBc%0ABvDzAD4D4EO3stGO4zgvBA5rgjgJ4N8AOI19wezT2F98Pzj//Cew78z92wAGAP4QwPcHtp/FcRzn%0ALuew+4B/8AafTwH82PzHcRzHeRaWNhpaQLx1QmccYSlImHdGS43jKh0QeUFvmDAX4rIst9cuSOSp%0A4ZqNTjZajzfjD9eJQ8XoRaasNzoTHQ/WTto29KzIo6PJAUAxjMWmFnZTPxNdhiNbb+10LCJWsILb%0AGkl59Lf+eixmbF+0Y/Gigb2flozZxpFYtBwQMfLovV9lyp74zCej4699jRUQJblsyo5skuhkly9G%0AxzuX7D2nsEJgqxwXGhKir4YVn5rW9rN2Cqhmdi4X9jSkfSVsEpGsrYnzBIn21zbKqaMkqbpIGbvv%0AVuUNSnL7PElKBEotsJE505K0SCyCoijVUuTZjw+KB+NxHMfpCF+AHcdxOsIXYMdxnI7wBdhxHKcj%0AllaE0zKcNpUzDY6795D0Oaqsqa1H277DX0zRj7ur17fiUH9oPdpWN46ZsuH6cXXtDVMnza0wV/Rj%0A8W6wQs4jggQTFbN+LGbkRLQq92z6nMnYihnZ5TiaF1Kr8pwurLh1ZScWYlaIsHnSOgQCqb3ve7/y%0Aa+M2EQ+tIyfuM2XrJ78iOu43nzd1Vk/aMXzyr2zYkquPx5HbqsoKbmlux2L1SNz3CZngWW499Mbb%0ANlJcotL6NMS7bLJnywrlIUoFqmCFM5pGSImK1cQ+T21p21BXZMfqIJ43klmhO5BUSft+Yc+QiG2D%0AJCRSLhEVK7W0lLO4b8qSuMAeAH8DdhzH6QhfgB3HcTrCF2DHcZyOWFobsCBR0Zi0TYyFLLJ2GCG2%0AtKqJ7ZPBxG4C+gPrbNArYptvv09SwhfWjtofnDBleT92oEgSu7kcLXGoSGLHBaFZLKxdq65sVC4k%0A8fBLats+nVm7+mjD9k2tUqHv7hC7emrL1jdje97olHU22N22qeQ3jr/OlOU91YeBRcKz8+HlX/tt%0A0fETf0Gitj1p40nV+RlblsRtTYi9cmXNzptMOZuwaGgJbLQ6SW1ZohwoyKUw3rF26LKKxzAhmkrI%0ASUSx0o6rfrdrK5LpgpWxDDZ6PpO08fq5AADJlLNEQrxPyD3WxNlkqmy+szqep1NyLwfB34Adx3E6%0Awhdgx3GcjvAF2HEcpyN8AXYcx+mIpRXhIG2UQkSLTWzbc0M2idcNSRukjPP9wnZDkVjxpEhj8aTf%0AIymDUhKpqbXiloT4WiLWSSEVK0jpNDFMZ2oqK7DM9nZM2WQnjvClN88DQJKTaGjrVuQr1eVb2wSM%0ASdnWOO774qTtq/ve9CpTtvniV5iypo7HnwmPLWzZymYsiN7z1/6OqXPu83bGbc++aMqSc4/GBTM7%0AJy9e3DZlm8fifhis27mVkih3+SUbpS1sxXM+IamTqomdOLOZTv9OopVZ/RVFzw5skqrnlUYcJCJf%0ARqKaqWdfpwcCgCSzwmZI42c4EGeQksz5nYlNw7U7i5/FbDV2zClBJvcB8Ddgx3GcjvAF2HEcpyN8%0AAXYcx+kIX4Adx3E6YmlFOIEW2mLvlJpELAqBpF4prFdLv4iVhEysF00erOCR1rHAlrQ2Ilfes2US%0ArDDXTtXdES+dZGiFn2ocq12zlAhniT1vsm3Fmr2LT8UFpP8GIytGgognW1e1gGPblZPocRsvj6OT%0AHX3ZcVOnmu2asvHVJ21bhy9RbbBiStNYrzrtWDXasB5up1/5babs4hP/wZStnonn25e/eM7UKadj%0AUzZCHEVvfZ2kmhra/ivO237Y21LiarCiqYB4S5bxuJJHDEJEOCGudqmKaidkTrakDYE8i6mabtRL%0AsLAiXN3E19/VSjGA7W0756elFYJ7G6ei441j8fFkxrzsboy/ATuO43SEL8CO4zgd4Quw4zhOR/gC%0A7DiO0xFLK8KF0CC0zxjuZ8rLSVLrDTPs29vp50Q1aFQYxsaKG+3MllVtfN7Kuk03M9iwoScz0i77%0AhcSlLbFiQ13GnlzTXRKCk6Rnme3a1DWTrViQaioShvEKERdIipuiiL+zv249+2pYz77+Wjw+SbBC%0AyXTrgikbkDRPk8txvZakayrHVoRrslh0G4zsuK5uvMSUnfyKr7PXn34qOs7O2/4brdm2F0fvjdtE%0A0uekq0T0HTEPMDW/K3utjIi3tfI4I8OMioSLTMXOXRMGNrOCW5PZZzMl4TVbNZ8D8VJtU5sKrFUh%0AKndqK0TvEk/FwcD285Fjp6PjtY14jvSmJNzrAfA3YMdxnI7wBdhxHKcjfAF2HMfpiKW1AU+mJcJC%0AapU8iw1SowGx95KoZilIWp8mdoxo9uzvoWbX2qIGK7FdkzkWZAN7XjGyts9WGdgSkkqeXR/KTtfU%0A1r7XzKw9arqzZcpme3FZMbAGvjGJTjXZscbBjdXYnjdYI1GtiA1TZXnCjNh7q10bPezq418yZRjG%0A4zMhdtTJFrExHok34598yVeYOnt7xFa4aSOyDY/FNua14/Z+Vjato0fTKIcAsbbqYs3qCytHrePK%0A+MnY+aOprUNKzuy7aWynZSnbm5ZENatJWh81T7PC2ntDxlIs2WclzVVa+sLa6ENunSfaOn6uk8LO%0Av9HA3uPaqr3W6lA5YUFHZ/S09I7jOHcUvgA7juN0hC/AjuM4HeELsOM4TkcsrQgneRNFXhoOYyN+%0AL7ebsYVEMIMQ4/w0NuqHPRYxzV5rcGwzOk77LMKTFSkS4gySD5RRn2xKz3Ii3qlIZDURRdqWpWay%0AUZ8aVS8v7P2sn7Qb/Rt7eczKWMwI21aY0Wl3AGCoxLq9c1YsbCp7j8N168zwpb+Mo7uNrlgxcnts%0AHUT+h7d+bXRc1vYGx1Myrqkds0TNy5XT95k6WWGj4+VNLJStDI+YOv2N06ZsePKirXf+bHS8R4RN%0AJhlp/x0qK4l9VohvBoIWqcj8lpyIcKQsLeI+TQd2DEEcONI2bsNq354nRHheWbHj0+vFz+JsEjvY%0AtDOiah4AfwN2HMfpCF+AHcdxOuI5LcAi8qCIBBF5aKGsJyLvFpGLIrInIr8vIvc896Y6juO8sLjp%0ABVhE3gDghwF8Wn30EIC3AHgrgK8DMALwfhGxO54dx3HuYm5KhBOREYDfAPBDAH5moXwdwA8C+J4Q%0AwofmZd8N4HEA3wjgDw76HaOVHvq9Z9bsXhYb4pvaruezyhrZcyLC9UNsUM8KK1D1jlvxaeXeWBgp%0AjtprI2XCHBH5lKGfRYFKhAxP0B44VjCqSpvCJyS2XtKLhbKEfF0xOmrKVhrb9+U4vlZLUhLNJraf%0AV5WnXc685Y7YsTj+yvtNWboS3+PF//uLps6Jr7ReaBsvjr3Jrl6xnnez0o5hRiJ8HX9RHDVt+yqJ%0AvkY8x5I8Fn1XTto/GotVOxajM680ZVcefSQ63sIXTJ3Q2rRIKRHYNELGlc35pB/3TdKzonnCPOGI%0ACAcl4CUJqdPadmlv0xUi3Kd9OxZpa8e1ncb1RNUR8v0H4WbfgN8D4D9dW2QXuB9ADuDhawUhhHMA%0APgvgjexCc5PF2rUfAPZpcxzHeQFy6DdgEXkr9hfaryYfnwJQhhCuqPIL888YDwL42cO2w3Ec507n%0AUG/AInIvgH8O4O+FEA4TgVjAtwsCwLsArC/8uGDnOM5dwWHfgO8HcALAJ+SZaEcpgDeJyI8C+GYA%0AhYhsqrfgEwA+wi4YQpgBeHpX87XrFlmB3oJ9cFeZrKYT2/TR0EZJ2iCZEwbKttqMbbSolTPWFjk8%0Ao2zAJE14IA4PQrIP6G3uIZCIUq3NppAmakO7WPtbSaJfVaXNiJErG3Det5vlizVr514nDiKznbit%0AQiJPDY9ZG+bwWBzhq79pM09IbjfGp5m1VA0243GtTjxl6oSjdiy2t2Lnj4rYe5vG9jNzEBlvPaG/%0A0dTpD23/9YZxRoe0Z/WMQN6XipGNhlasq7KMZJAwJYAoG3BK5m2Ws6h9tl6qssA0xHacEgclye0z%0A1SC2+ZY1SUtf2sh39TR+FpPK3nWunycAoSHPaxWPv45UWIXnJxraHwJ4HYDXL/x8HPuC3LX/VwAe%0AuHaCiJwG8FpcZwF2HMe5WznUG3AIYQf7gtrTiMgegEshhM/Oj38NwC+IyCUAlwH8PIDPANCCneM4%0Azl3N7YgF8RMAagC/DWCA/bfm7w8h3JyztOM4zguU57wAhxC+QR1PAfzY/MdxHMe5DksbDW13N0Fd%0APmOirlXq+JEWGgAcPWajRW0e3TRlqRK8QmkFjwFxsuitxvWywoopEkhUJiI2BOVAEXQabwAt2bCv%0Az6squ6GeCW5NYwU9UdHPiqM25U1BIkMJidQ1OB5fKyFijRDBowmxQCS5Fe+YMFNOreixeznemNMW%0Adly3r9r+Kr/wl/HxzAp8bKxHG3asp7vxDkySaYpGnSt6qm8SIgSSPyLTgqXAisXofEgi2m0/aRum%0AmlX0rUMCE2qznpWSRDmptMRZg6XvykY2vXyNeI6QYHXoE7Fz0FPt18cAQknE7yn5AonnVqb6gTlb%0AHQQPxuM4jtMRvgA7juN0hC/AjuM4HeELsOM4TkcsrQiX4DiShZxEG+uxsHDkpBWM1o5aAae/YsWT%0ALFHpc4gAxrzcoD2DyK8vJjQhZZE4VfQwYsNvK5JGqIzFtLK0kbuq6Y49r7XXyvL4BnobJ00d7fED%0AAFljxZNWeQAyz77QWO/1Wt1jO7XXnuzZiGIIVkxrSiU2lXaAxpfseUkeR48rifjZ9qywuT0jAs4s%0AvtbqEev9x9L6zKbx9WmKKiIEJpl9hHvrsfAcWGorIZHIVHf1CtKGgf2+wCIA6osl9hnorVihO12x%0Az3A9i6/fEE+1jDw/Oq2YbNh+mFZ2XOvpjedpT0V3S8kachD8DdhxHKcjfAF2HMfpCF+AHcdxOsIX%0AYMdxnI5YWhHuyNGTGPSfMXSPNmOD/eoRG3pSe6cAQJpZgUBUGUsHJFQ4U4Z2ang/2O+0VqluCRFm%0AmJA13Y0FqeneJVOnntpwlCCCXpA4hF9CxJqsR8IDVkR0aeOytraed4GkeqmmsWhVz2zbyz07Tfcu%0A2765+FicgujyYzovAJDk1itsfSueN6snX2Tq9Fes99/4Cgl3qdy0Qm2919rE9t/Jl74iOs6Jh1uW%0A2bnVI6LYYDMW/nqbNiTr+In/z5RJUNdnjwBpOwuTqZ+DtGfnVjqwz7Dk1nsxUXOrD3utgqSHyleU%0AB93YhqxsGjs+LHulFqwT5amojw+KvwE7juN0hC/AjuM4HeELsOM4TkcsrQ24N+ijv2AD7qtIZPRX%0AB7GZttquBUCU7bYlqUpCZW2YiUr/E5jdR0iyF5I2yOx616GoYJ0bAKAcxzbT6e6WqdOSFPQp2bCv%0Ao7RlxAbMbOFJS+xmKqc9cxpoGpYIR9vlbNuriXWeQGs30Cfluej4xKrtm2yV2CI3Y8eFfGDt3rPd%0Ay6asYbZ2Za+8snPRVBmRCH3TcXyPaWHb0EuIIwbpr0TZaROmZ6QkTbyZuywaHyuzz5guS3IS5Uxs%0AmcDavlc2Yrv9cMWel9P0RiotUkMiDpJnOBmQFE6qTys19hVx3jgI/gbsOI7TEb4AO47jdIQvwI7j%0AOB3hC7DjOE5HLK0I19Qt6igqVWwsZ04KbSCCEanXlEqEIyJPM7PiRliPxYD0iDX8a6EOAALZ2a0F%0AvCbY72NphOombmvTklRDRHORxP6uTbJY1AlECGS5VElgK4hyJJlNSCQ3EsVKEKc8mu5ZYYtlc10/%0AY8WaXhafu/M4iWpFUh4Vq7GTT5oSZ5BdG5GtmdmN/dOZiu5GhJ+EpZ9qVKqpqRUZS5IiCGTelONY%0AMExhxwJE4E3UWBP9mg8Ga5YSZaWwkc8aIrgNB9ZRZvN0HKWvv2rTZJHHHCFo4cw65gTi3MIeIMnV%0AtWbx3KpL+xweBH8DdhzH6QhfgB3HcTrCF2DHcZyO8AXYcRynI5ZWhAshDjbWqGheLMpZaFkZ8ZBR%0AYlNTWiFjcsl6UQUluhQDErmJRGoC8RyDEl0a5vU2s6mFWhXBLBsQ4TG3ZS3xYBLljccc9pKETBEi%0AdqZFfP20sr/bK+JxuHsp9uzbedIKJSDpc1bWSfqpjXui41WxHmez5l7brjoe6/FV6/WmPRAB7kGJ%0AJG5rRqKaaS8qAJhuxfed9+15THBDa/u5vPrl6DhtiSchiWqmnzEEWychEe3IY4dWeUJWwXr2JbDP%0AZp9E3xuOYtFNiHBWzezzI8qzs1i3HnSDk3YetVOyjiTxM7z3VCzKtkSQPQj+Buw4jtMRvgA7juN0%0AhC/AjuM4HbG0NuCklyHpPdO8WkXSysnO67q0dqC2tPbXQkW7EpICPCf2XZ0QY7Zt7YLlVWu3tVGm%0AYGxwVWntglVjN+MjjTd8pwWxx7KsBcRmXqtsADWxhac5yRZCsndo5wwSbAspMZMlWdyG3qodi9mu%0A7b+rl+zG91bNkeHQZrFoajtHxltxxLJQ27EIMzvWTUVs+1k8bxriBLGanzBluk/rkjiRkGwhk0uP%0A2rKLj0THidh5lPfsfKiUg5K0xImJlJXM+SiJ7a1FYR0s+gPrnNFftWVBPT/jSyQyXW3boAOwpbmd%0AlP0j1gY8u8ps5vFzUM2eiI/dEcNxHOfOwhdgx3GcjvAF2HEcpyN8AXYcx+mIpRXh0iJDtiDCiYpQ%0ARFNhVyQyFNn0nqn0PCxSWL5iN4RnvbgNTWNVpb2z1pGg2bWCig64NJkSp4vMCjj9I3Hbh0dtO9Gz%0Aw1oT8Wm6F7drRiKRZcQfQFIrlKUqslpWWFGkGNp2DZUDSlYQ0XRoy6YT2/dBbfaf7ljBaLZrBSnt%0AgCC1FWEkkKhzYufbcC0W2JKBdQapa5J2Sc3dQFJN5QVxGHriz01Z2I1FuF5ux55pzPVuPGYpeS7S%0A3I5hUlgHh97m6eh4tGGFx2JIHJmIE1GjnJbKCRO8bLsyFXVOSPqhbGgn+HTXjn+rBP58Lb7nemaf%0AiYPgb8CO4zgd4Quw4zhORxxqARaRd4hIUD/nFz6XeZ1zIjIRkQ+LyGtufbMdx3HufG7mDfjPAZxe%0A+Hndwmc/BeAnAfwogDcAOA/ggyJid2E7juPc5dyMCFeHEM7rQhERAD8O4J0hhN+Zl30fgAsAvgvA%0Arx7mS5pZiXrBwyYv4qa2rTWoB5JGqJmQsqESPEqWz8SW2dQ1RJAgHmfbl7ZNWa2EnmlpRTjp23uU%0AYj06zkcs8hkRrXasEDhRZeXYCltrx6yIBCLOBBOVi0RpI7/ue8PYO6k3sN5Ks7Ft+5BEZGva+Nxx%0A397PNvEunCkPOhMVDIAQjzaiFyFV87RYsZ5ddck8reIxy4mQGmbnbLtIWYp4LjXkWSl6JO1OEvdD%0AVtixSIl6N1g/Y8rWTsSR6for1uOMrT4hJZNElSXEO5PlT2qV1x5LF8ZERRBvv1qJpMPjystyaufo%0AQbiZN+BXzE0Mj4jIb4nIy+bl9wE4BeDhaxVDCDMAfwTgjTfVOsdxnBcwh30D/lMA3wvgLwGcBPAz%0AAD4yt/Oemte5oM65AOAl17ugiPQALP6qdXOF4zh3BYdagEMIH1g4/IyIfBTAFwF8H4D/eq2aOk1I%0A2SIPAvjZw7TDcRznhcBz2oYWQtgD8BkAr8C+4AY88yZ8jROwb8WLvAvA+sLPPc9S13Ec5wXDc/KE%0Am5sPvhLAHwN4BPuL8AMAPjn/vADwZgA/fb1rzO3ET7u2yNxQvnt5C03vGWN7MYg9TdLMigiBvGi3%0AjS2rxsqThtRpiRBTjGLjf75hrSXDE1ZsqKf2Wns6umFF/khIrZiWFHE/NOz+dq2n0M5lKwROduK0%0AKnuXbTql9dM2pCNT00T9Lg/a1Q9Ay0KIqvbXJLVMOSWeaYn1AGx0uhziqdazTlvQmuWUibIkrRT7%0As057R072niLn2XZtjmJxtT+wdXb/6mOmLNk9a9sw1eNvx6IgqaygxK1Awjemg3VTNjjyIlu2Fj8H%0AgbShJp6kDUu7pFJSJYVdtsqJnTdBzSXJ7P00NQsVe+OUR72eupbc3LvsoRZgEfl5AO8D8Bj232x/%0ABsAagF8PIQQReQjA20XkCwC+AODtAMYAfvOmWuc4jvMC5rBvwPcA+D8BHAPwFPbtvl8TQrgWFfrn%0AAAwAvBfAJvZFu28KIdg9Vo7jOHc5hxXh3nqDzwOAd8x/HMdxnGdhaaOhNXWLJn3GPtMq0xAxJ0JI%0A+vKKbZBWka3669b2mRP7l0kjNLO21oakRcpH1l45Wo1tq2VNbKYkalaiNtBXJOXSdM/aTHe3bEqd%0AahzX2z5/0dQ5dh+JYkUixem0MXVpHR6sswaQqk320rdj0ScRq8qSbLxv4r5hG+9ZBDudXr6eELs6%0AibRH9usjyeJ6K0ftPOqtWkP06Khqe2XHq53aSHvtnrXtl9O4Yb3hiqnT69v51lPzNATb9mRgNY7e%0AyOoEopyUGqZxUC3B1mv0c5DacU0yu5TpFFXjS1dtHTInJbGRzcrdeN7Uddzvk9nz54jhOI7j3AJ8%0AAXYcx+kIX4Adx3E6whdgx3GcjlhaEW64uYZB/xkRQJvmKxK5Kyf5c9hmeb2petSzEavSHhGMVISq%0AprZXH1+24lM9tql+TIBOspG7rKzAlqo7ms2s4DYb27KSOIM0Kq3P7kUrws2IoJeRiGWJiuaVEqEk%0AZFbcyCUW3Sbk+8rKjrUkdqx1dLqU7OnPC6ucpdq3gEyaQKJtVVPbrv5afPJw0/ZDf9X2QzWO+37n%0A0c+ZOrOrNk1RO7HiT39Fpcup7TxqazsnB/24rdOSREwjz5gkRABTz4aOTAYAQgaoJQ4vlWqHCJlH%0AA9uuuozbsEeckZKeje6Wkmhropw/kjxuQ9LYdh8EfwN2HMfpCF+AHcdxOsIXYMdxnI7wBdhxHKcj%0AllaEkyyFLEQ8C8prhkU/qgMxhBNxK+9rMc0KBG1rr2/c7yp77d2nrKF/um09mKoLSsDJbRv2dqyg%0ANzquRIPUKkY1E++I15HWRapdK8yUe1bkGRyxwpIYrzOWksiKG40SiMqp9QBbWSMR5mrbhtk0FnWm%0Ae/Z+0tT2cz6Ky0ZHbcSvyVHb9um2FQx132Q9EtXsik0j1O5ejo53Hv28qVNu2/nQL+xYZ4lKuUVE%0AK+bFWRSxJ9y0IREHSZQ7Ot9UiLlA0mRlfTsWgYh1OuJfQsTcNLHt0kJwf4Ok1yKiovagA4C1M8oj%0AVAmPMrFz7SD4G7DjOE5H+ALsOI7TEb4AO47jdIQvwI7jOB2xtCJcXdeoF0I05q1KSdQjni8kFU9L%0Awgj2VGqhhtSZXbWh64IK/ajDGALAzo71Vtp+6pJtq/KOSwv7u3BcWgEsVbfdXyNpY1J7rWxghQuM%0A4/ZPt2zc/MuP23R+w2PHTFlQnoMh2LazrC1awBmMmDej7eeyZF5UWgCz95yIFUt6g/i84ar1jlpZ%0As42fjW1YztlUpViq7HzIe1ZAHF+MxdvplcumTk48zgoiSG1djscxI+9ZFYmeKFnslZjl9toCIuix%0AUJ2IRew2ENFvaNsVWhJqUuI+DcQDcTYjZTtxu/KRFVclsd+3n0dYlZgwsCqEKYuPewD8DdhxHKcj%0AfAF2HMfpCF+AHcdxOnMABcAAABEDSURBVGJpbcAiCWTBaKhTyQ/WbJqVYmTT2VTBbpZvm9g+Ve9Y%0A+9Hel4jddjc2nO2OrSEtP2Hth/0j1la4raJYZSRlS69P0mir/eyTbduGomc3pQ/XSYSnYWzP27pq%0AbXlXzj5hytbO2BQ0o+NH4zYMbdodEXuPaRrfkBD7W5rZ+xms2KnbqA30ZWI3/ydkw/5wNZ43iRAH%0AAeLAAVKvUZHb0ty2sxpbZ5Mr574cHV+6aJ0uVohNW6fqAoCiiMf6yhZJk0Ue/WI1fh/LiM4SUvuM%0AgThnlMrRo63sc9gj1xd2rZ3Ypj3bsvbkmjhmVXsqNdOGdegpjlnnjHzdri1tE3d0PYuPm9K26SD4%0AG7DjOE5H+ALsOI7TEb4AO47jdIQvwI7jOB2xtCJcPZmiXoiMtHMpFiV6LycRkViUpMwKPzMVZWx2%0AwTpdXP28jViV5vHvq11ieM97VtA79hLruNCUsWjAolP1Vsj9KIeHnfN2o3+fpFMartpN6HlfiyAk%0AxdKFp0zZ7nnbN2snY2EuBHutqrR90zZatLLCY1sSRwwSfUp/Y02+b7BKInwppxFJbNvZ/bTBPj6i%0AnGAme3ZuVVetk4XsxaLvgLwapbUVmsqprTi5Es/vnKSHQkpSVE3juRRgxaiECKJCPGxq5elR5LYN%0ABRGZ68o+B1cfj9M1lZdJlLtg21X04vbvnLUpt5KL1vloeO8JU9Y/EQt4Riu8yVdZfwN2HMfpCF+A%0AHcdxOsIXYMdxnI7wBdhxHKcjllaEm17dA3rPCAWTy7H30M4F66mWD63H2e6Xbb1Epa7ZfsIKWbMt%0A6620ca/ymmmssLB3yRr1R8esV5gWdXqr1sNocNyeV6moT83EentNxtY9anrMClJ95TmYDawogpkV%0APPbO2z7dPhWXrZ4iAguJ7pYVKspdSjzHKiIYNdazSlTqnZZEqCIZb9AoIdCmVwJq7YIIoK5svcmO%0A6i8i3k2v2BRVOvXTHhnDmqTAGhDBVTvoNbltQ5Fb0apqlRjZ2vRaxart96Rv+0ZUCqy0ICmqmGhO%0AUmyt33smOh73bLv2zpI+ncXXEpISq9qyc3IHViRFHp+br8bzm6VEOgj+Buw4jtMRvgA7juN0hC/A%0AjuM4HbG0NuDJrIrNZ8rcNj5vba3FhrWbnfvvNppXq7IpZCnZxF3Yrglqk302INGiWmvXGm+TSEkq%0AE0RDjJPWog0E1RHSt9+XkRT0QrIbJP3YBpyvHTV19p74sinbecra2/qPx/0cEmsDzvrEcSFZjY7r%0AxkYBC8HeTzFgNre4jNtt7Vjo4S/JeW1D3lWCtQG36tRqz9rQJ5dI/6nhYc4NQxJZrVeQTCeqWmEc%0AboBAMkEUao7kJPpaSIhdvSaOK6ofmpJoFbu2b3KihaycjLWQgjgVpb1VU7b9RGwrHqxaTaW8bO3J%0AFYmstvVo7MTRPxbP78mMpBg5AP4G7DiO0xG+ADuO43TEoRdgEXmRiPxbEbkkImMR+ZSI3L/wuYjI%0AO0TknIhMROTDIvKaW9tsx3GcO59DLcAisgngTwBUAL4VwKsB/EMAixFHfgrATwL4UQBvAHAewAdF%0AxBppHMdx7mIOK8L9NIDHQwg/sFD2pWv/kf0d7D8O4J0hhN+Zl30fgAsAvgvArx70i9ZOrWOwIB6M%0Az8XG8r2nrAiXblqxITlqy3afiDeTrxDBI5DMK5cvx5Gt8r6tlGUkffkeiXSmhJFy1zpKXL1oBYJc%0AiU/rxMlDiANC2rNDnQximW90+qWmzpQILOPxk7bsqThqWrZi27V6hkSFU+nKUyIOSWLF1YY4wQRz%0A3yS1UGsFFu3goNPPAEBTs4hfJB+QSsdeTaxDT1VaZwaoyGplY9sZiDjYEC1yOIjFs9GmFURTIswh%0AjdNplZWVgRvSN9WOnd+Ncqjpr9pr9dbsO1lCoqZpwTBfsc9db8P2zZHV2HFKp4sCgEuPW5E+CHFI%0ASuJzL/zZ2eh4Rq59EA5rgvh2AB8XkX8vIk+KyCdF5IcWPr8PwCkAD18rCCHMAPwRgDfeVAsdx3Fe%0AoBx2AX4ZgLcB+AKAbwbwKwD+hYh87/zzU/N/L6jzLix8FiEiPRFZu/YDwE0VjuPcFRzWBJEA+HgI%0A4e3z40/OBba3AfjXC/X0361Cyq7xIICfPWQ7HMdx7ngO+wb8BIC/UGWfA/Di+f/Pz//Vb7snYN+K%0Ar/EuAOsLP/ccsk2O4zh3JId9A/4TAK9SZa8E8Oj8/49gfxF+AMAnAUBECgBvxr6AZ5jbiJ+24l+L%0ARNWolETSU5GNrMaDJreG8NWXWOP/+olYgNh53EZDK3eIZ4sSpMLEiilT4tEmFfFWG8VdP0usiJCR%0AyF21iuQWJiTNT22FksFx2w9FLxYzhqOhqaOjWgHA1lkrEE22Yu+u9Knzpk5vw14fKvqVEPe/jETu%0AYimCQquuBeYJZ/urUV6JIZDoayQSWTUhf9TpdpGobUfPbJiy6cV4Dm6M7ODPSPS1om/LMonbMB3b%0A+yEB0qCzQfWJUDerreBWs0dF9Wmb2v7Lh1ZMC2TMGpWKaeecTS109Zz1LhydPB4ds7Rfq/day+hk%0ASrxSj67FbVLrUUbSkx2Ewy7A/wzAR0Tk7QB+G8D/COCH5z8IIQQReQjA20XkC9i3Fb8dwBjAb95U%0ACx3HcV6gHGoBDiF8TETegn2zwT/G/hvvj4cQfmOh2s9hP4zBewFsAvhTAN8UQrD7xhzHce5iDh2M%0AJ4TwfgDvf5bPA4B3zH8cx3Gc6+CxIBzHcTpiacNRPvaZL6GXPdO8WRkb4hPiFXQUNkzd+pk1UzZY%0Aj9WG4YikMnrChkWcXonD5+V9+/urrK3gIQMrwhXKa29wnIThI+1KlddePbXfd+WiFSQCSZmSqvCG%0AWc/W6Q1XTFnWtwpouxOncal2rLA5vUysUKpdLfFwyzI2TYn3ohJw2tqKKeXYhkBMldqZ9az4VE+t%0AeFfP7Byc7saK1OioFdyKzG5137sQ91dOXo1mRJTNSAqnSRn3YcjtHMmIE99MlVVbVuzKBrZhSXrG%0AlFVl3IeTXavUXSWprVbW7Xyrlffi5cfJhqraPmOXH4uFYBqCc2jncrFOnjvlgXrsZSej48nUw1E6%0AjuPcUfgC7DiO0xG+ADuO43TE0tqA9y6PUS3kihkOY7ttS9KxX/ocsX2SaF79l8dRkgKJmsXSY2fD%0A2A40WCd22751NtD2awBolMGtSEj6F5KOHUOVNmZkz1tpiA2LRGlrlMMGdXiw3QwRe9+1Ss8TSNSs%0A2Y61Aeej2AYnQtKl71n7WlvbhiVZbHdkNtpyah0jhmtqblXsPHs/JOgcgnLEacXakyd7xJFlrM8j%0AtvDUlk13bFv7SpvIidPK1JrCERrlyELOqyrrYBNGNm1Vkt0XHU92ScS0XRspLiHvhNkwLuut2meM%0ApQIbbcaaUE3SBl181Nq5h8et3f6pL8f1Vo7E89ZTEjmO49xh+ALsOI7TEb4AO47jdMTS2oB1avBU%0A2Stbsg/Y5K4HMCNZCyYzlbWAbLBkdlt9rYTUScheQ3atRNvzyK/ClpRpU66Qe9b3BwAgKc1TFcin%0AIdcak/2vE71hFEBVxn2YkD4NxI6aqBTgGUlBz4ILsfHXfVqTVOgl2TetO1WI/bUk98xswDN1P4HY%0AbVk/TFT/tZW9eE2C8YSG9LMyo7elPY/ZmPW1mA1YWtungcy3SRLbfAMJxtPAnjcm+2kztfd9QoLq%0ABNKuZhrb9pkNeEqC6MgB6iWz+HmakjYdBGFRpbpERF4E4OwNKzqO4ywf94QQrCp5HZZxARYAZwDs%0AYD87xlnsxwi+04L5eNu7wdveHXdy+29F21cBnAuHWFSXzgQxb/yXgehPwZ0Qgs1QucR427vB294d%0Ad3L7b1HbD32ei3CO4zgd4Quw4zhORyz7AjwD8H9gIWXRHYS3vRu87d1xJ7e/k7YvnQjnOI5zt7Ds%0Ab8CO4zgvWHwBdhzH6QhfgB3HcTrCF2DHcZyOWNoFWER+REQeEZGpiHxCRL6+6zYxRORNIvI+ETkn%0AIkFEvkN9LiLyjvnnExH5sIi8pqv2LrTrQRH5mIjsiMiTIvK7IvIqVacnIu8WkYsisicivy8i93TV%0A5kVE5G0i8mkR2Z7/fFREvnXh86Vt+yLzcQgi8tBC2dK2fT6Xg/o5v/D5Us73a4jIi0Tk34rIJREZ%0Ai8inROT+hc+f1/Yv5QIsIt8J4CEA7wTw1wD8MYAPiMiLO20YZwXAfwPwo9f5/KcA/OT88zcAOA/g%0AgyJiMzM+v7wZwHsAfA2AB7DvFfmwiCxmRXwIwFsAvBXA1wEYAXi/sKjpzz9nAfwjAF89//nPAH5v%0A4WFZ5rYDAETkDQB+GMCn1UfL3vY/B3B64ed1C58t63yHiGwC+BMAFYBvBfBqAP8QwNWFas9v+0MI%0AS/cD4E8B/LIq+xyAd3Xdthu0OwD4joVjAfAEgJ9eKOvNB/zvd91e1fbj8/a/aX68DqAE8J0Ldc4A%0AaAB8c9ftvc49XAbwg3dC27G/qP4lgG8E8GEAD90J/Q7gHQA+dZ3Plnq+A/inAP74WT5/3tu/dG/A%0AIlIAuB/Aw+qjhwG88flv0XPiPgCnsHAvIYQZgD/C8t3Ltfwt1/LL3w8gR9z2cwA+iyVru4ikIvJW%0A7P818lHcGW1/D4D/FEL4kCq/E9r+ivmf6I+IyG+JyMvm5cs+378dwMdF5N/PzW6fFJEfWvj8eW//%0A0i3AAI4BSAFcUOUXsN85dxLX2rvU9zKPQPeLAP5LCOGz8+JTAMoQgk60tzRtF5HXicgu9r2XfgXA%0AW0IIf4Elb/v8l8X9AB4kHy9127H/1+n3AvhmAD+E/TZ9RESOYvnn+8sAvA3AF7Df/l8B8C9E5Hvn%0Anz/v7V+6aGgLaBc9IWV3Cst+L78E4Kuwb2+8EcvU9s8DeD2ADQD/M4BfF5E3P0v9ztsuIvcC+OcA%0AvimEcJhMjp23HQBCCB9YOPyMiHwUwBcBfB+A/3qtmjptKdqO/RfOj4cQ3j4//uRcM3gbgH+9UO95%0Aa/8yvgFfxL69S//GOQH7m2nZuaYOL+29iMi7sf+n2d8IISwGwj8PoJgLF4ssTdtDCGUI4a9CCB8P%0AITyIfTH0H2C5237/vB2fEJFaRGrsC6L/2/z/F7C8bTeEEPYAfAbAK7D88/0JAH+hyj4H4Jq4/7y3%0Af+kW4BBCCeAT2FfmF3kAwEee/xY9Jx7B/qA+fS9zG/eb0fG9zLfb/BKAvwvgb4YQHlFVPoF9tXix%0A7acBvBbLOw6CfdFkmdv+h9jfNfD6hZ+PA/iNhf8va9sNItID8JXYX9yWdr7P+RMAr1JlrwTw6Pz/%0Az3/7u1Ymr6NGfif2leD/FfuD+88A7AJ4SddtI20d4ZkHKQD4ifn/Xzz//Kexr6K+BfsP0W8COAdg%0AteN2v3ferjdj/zf+tZ/BQp1fBvA4gL+F/e2AfwjgUwDSJej3fwLg6wG8FPsL2jux/5fTA8vednIv%0AH8Z8F8Sytx3Az8/nzH0A/jqA92E/EPlL5p8v5Xyft+0N2P/l9nYALwfwXQD2APy9hTrPa/s7n3zP%0A0lk/AuBL2BdYPoH59qhl+wHwDfOFV//8q/nngv2tO08AmGJfUX3tErSbtTkA+P6FOn0A7wZwCcB4%0A/rDd23Xb5237tYX58SSAD11bfJe97eRe9AK8tG0H8FvzBanEfuaa/wjg1QufL+V8X2jft2HfZDLF%0Avvnhh9Tnz2v7PRyl4zhORyydDdhxHOduwRdgx3GcjvAF2HEcpyN8AXYcx+kIX4Adx3E6whdgx3Gc%0AjvAF2HEcpyN8AXYcx+kIX4Adx3E6whdgx3GcjvAF2HEcpyN8AXYcx+mI/x8AgYymeHEWQQAAAABJ%0ARU5ErkJggg==" alt="" />
- 许多深度学习里的bug来自于矩阵/向量维度不匹配,如果你能保持你的矩阵/向量维度清晰,你可以消除很多bug
Exercise: Find the values for:
- m_train (number of training examples)
- m_test (number of test examples)
- num_px (= height = width of a training image)
### START CODE HERE ### (≈ 3 lines of code)
m_train = train_set_y.shape[1]
m_test = test_set_y.shape[1]
num_px = train_set_x_orig.shape[1]
### END CODE HERE ###
print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))

Expected Output for m_train, m_test and num_px:
| m_train |
209 |
| m_test |
50 |
| num_px |
64 |
2.3 转换矩阵
- 最终,整个训练集将会转为一个矩阵,其中包括num_px*num_py*3行,m_train列。
Exercise: Reshape the training and test data sets so that images of size (num_px, num_px, 3) are flattened into single vectors of shape (num_px ∗ num_px ∗ 3, 1).
其中X_flatten = X.reshape(X.shape[0], -1).T可以:将一个维度为(a,b,c,d)的矩阵转换为一个维度为(b∗c∗d, a)的矩阵。
X_flatten = X.reshape(X.shape[0], -1).T # X.T is the transpose of X
# Reshape the training and test examples
### START CODE HERE ### (≈ 2 lines of code)
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
# 基础方法:需要的是 m_train 行 (shape[1]*shape[2]*shape[3]) 的数据, 所以需要转置,不知道为啥算出来和上面的方法不太一样。。。
# train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[1]*train_set_x_orig.shape[2]*train_set_x_orig.shape[3], train_set_x_orig.shape[0])
# test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[1]*test_set_x_orig.shape[2]*test_set_x_orig.shape[3], test_set_x_orig.shape[0])
### END CODE HERE ###
print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
print ("sanity check after reshaping: " + str(train_set_x_flatten[0:5,0]))
# print ("sanity check after reshaping: " + str(train_set_x_flatten[:, :]))

Expected Output:
| train_set_x_flatten shape |
(12288, 209) |
| train_set_y shape |
(1, 209) |
| test_set_x_flatten shape |
(12288, 50) |
| test_set_y shape |
(1, 50) |
| sanity check after reshaping |
[17 31 56 22 33] |
2.4 预处理数据(去中心化)
- 为了表示图像(RGB)必须指定为每个像素,实际上像素值就是三个数字组成的向量(0-255))
- 通常机器学习的预处理工作是 去中心化和标准化你的数据集, (x - mean)/标准差。但是对图像数据集,数据集的每一行除以255(最大值的像素通道)更简单方便高效)
train_set_x = train_set_x_flatten / 255.
test_set_x = test_set_x_flatten / 255.
What you need to remember:
常见的预处理一个新数据集的步骤是:
- Figure out the dimensions and shapes of the problem (m_train, m_test, num_px, ...)
- Reshape the datasets such that each example is now a vector of size (num_px * num_px * 3, 1)
- "Standardize" the data
3 - General Architecture of the learning algorithm(算法流程)
- 设计一个简单的算法来区分猫的猫图片的图像。
- 你将用神经网络的思想构建一个逻辑回归,下面的图像解释为什么逻辑回归实际上是一个非常简单神经网络!
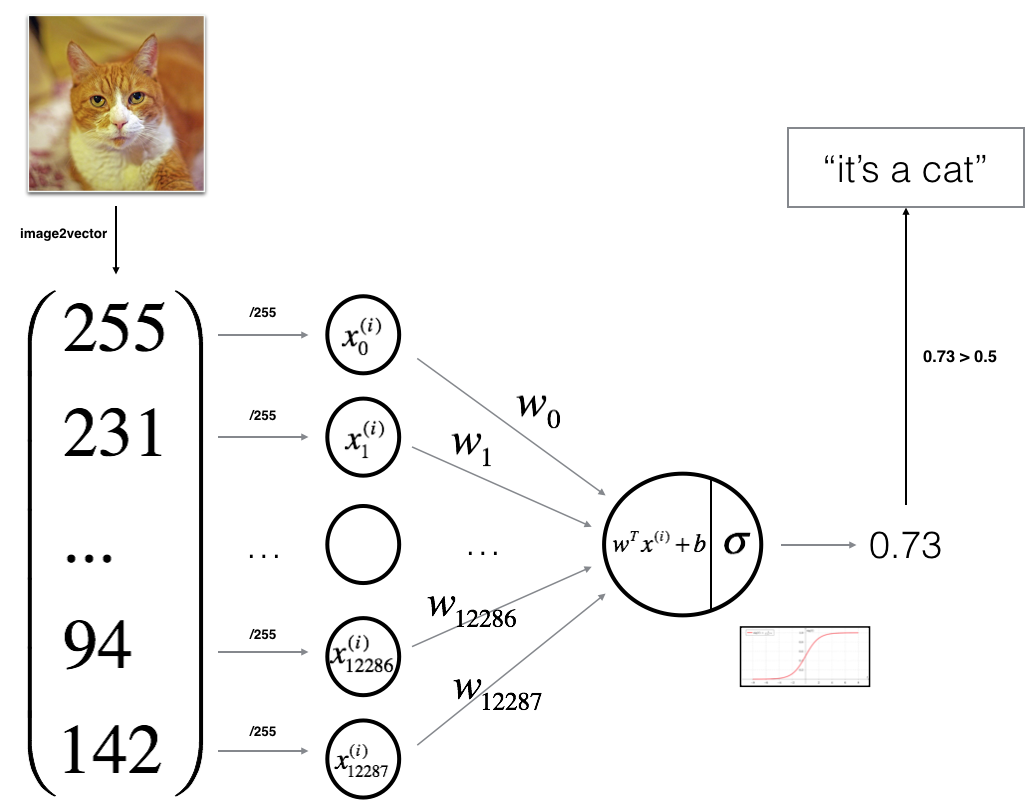
算法的数学表达式:
对一个 样例 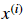
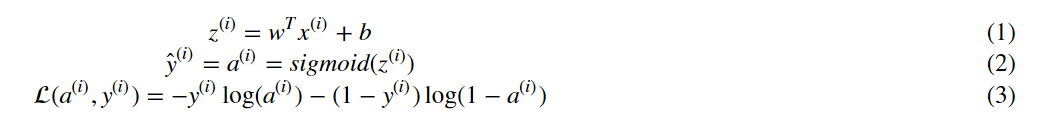
计算所有训练样本代价:

Key steps: In this exercise, you will carry out the following steps:
初始化模型的参数
通过最小化代价来学习模型的参数
使用学习好的参数来进行预测(在测试集上)
分析结果并做总结
4 - Building the parts of our algorithm(构建算法的部分)
搭建一个神经网络的主要步骤:
- 定义模型结构(例如输入特征的数量)
- 初始化模型的参数
- 循环操作
- 计算当前的 loss 值(前向传播)
- 计算当前的梯度值(反向传播)
- 更新参数,梯度下降算法
你通常分别构建1-3.并把他们集成到一个model()函数中。
4.1 - sigmod()函数实现
Exercise: 实现 sigmod() 函数, 你需要计算 sigmoid(wTx+b) 来进行预测
# GRADED FUNCTION: sigmoid
def sigmoid(z):
"""
Compute the sigmoid of z
Arguments:
x -- A scalar or numpy array of any size.
Return:
s -- sigmoid(z)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1 / (1 + np.exp(-z))
### END CODE HERE ###
return s
print ("sigmoid(0) = " + str(sigmoid(0)))
print ("sigmoid(9.2) = " + str(sigmoid(9.2)))

4.2 - 初始化参数(w, b)
Exercise: 在下面实现参数初始化. 你不得不初始化 w 为一个零向量。使用 np.zeros().
# GRADED FUNCTION: initialize_with_zeros
def initialize_with_zeros(dim):
"""
This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
Argument:
dim -- size of the w vector we want (or number of parameters in this case)
Returns:
w -- initialized vector of shape (dim, 1)
b -- initialized scalar (corresponds to the bias)
"""
### START CODE HERE ### (≈ 1 line of code)
w = np.zeros(shape=(dim, 1)) # 初始化 w 为 (dim行,1列) 的向量
b = 0
### END CODE HERE ###
assert(w.shape == (dim, 1)) # 判断 w 的shape是否为 (dim, 1), 不是则终止程序
assert(isinstance(b, float) or isinstance(b, int)) # 判断 b 是否是float或者int类型
return w, b
Expected Output:
对于图像输入,w的维度是 (num_px * num_px * 3, 1)。
4.3 - 前向传播 和 后向传播
现在你的参数已经初始化,可以进行 前向传播 和 后向传播 步骤来学习参数。
Exercise: 实现一个函数 propagate() 来计算 代价函数 和 他的梯度
Hints:
Forward Propagation:
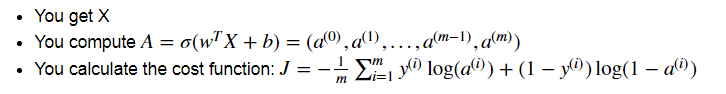
Here are the two formulas you will be using:

# GRADED FUNCTION: propagate
def propagate(w, b, X, Y):
"""
Implement the cost function and its gradient for the propagation explained above
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)
Return:
cost -- negative log-likelihood cost for logistic regression
dw -- gradient of the loss with respect to w, thus same shape as w
db -- gradient of the loss with respect to b, thus same shape as b
Tips:
- Write your code step by step for the propagation
"""
m = X.shape[1] # 样例数
# print(m)
# 前向传播(Forward Propagation) (FROM X TO COST)
### START CODE HERE ### (≈ 2 lines of code)
A = sigmoid(np.dot(w.T, X) + b) # 计算 activation , A 的 维度是 (m, m)
cost = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * (np.log(1 - A))) # 计算 cost; Y == yhat(1, m)
### END CODE HERE ###
# 反向传播(Backward Propagation) (TO FIND GRAD)
### START CODE HERE ### (≈ 2 lines of code)
dw = (1 / m) * np.dot(X, (A - Y).T) # 计算 w 的导数
db = (1 / m) * np.sum(A - Y) # 计算 b 的导数
### END CODE HERE ###
assert(dw.shape == w.shape) # 这些代码 会 减少bug出现
assert(db.dtype == float) # db 是一个值
cost = np.squeeze(cost) # 压缩维度,(从数组的形状中删除单维条目,即把shape中为1的维度去掉),保证cost是值
assert(cost.shape == ())
grads = {"dw": dw,
"db": db}
return grads, cost
w, b, X, Y = np.array([[1], [2]]), 2, np.array([[1,2], [3,4]]), np.array([[1, 0]])
grads, cost = propagate(w, b, X, Y)
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
print ("cost = " + str(cost))
Expected Output:
| dw |
[[ 0.99993216] [ 1.99980262]] |
| db |
0.499935230625 |
| cost |
6.000064773192205 |
4.4 Optimization(最优化)
- 你已经初始化了你的参数。
- 你已经能够计算一个代价函数和他的梯度。
- 现在,你需要用梯度下降算法更新参数。
Exercise: 写下 optimization function(优化函数),目标是通过最小化代价函数 J,学习参数 w 和 b。对参数 θ,更新规则是 θ = θ - α dθ,α是 learning rate)
# GRADED FUNCTION: optimize
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
"""
This function optimizes w and b by running a gradient descent algorithm
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat), of shape (1, number of examples)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- True to print the loss every 100 steps
Returns:
params -- dictionary containing the weights w and bias b
grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
Tips:
You basically need to write down two steps and iterate through them:
1) Calculate the cost and the gradient for the current parameters. Use propagate().
2) Update the parameters using gradient descent rule for w and b.
"""
costs = []
for i in range(num_iterations):
# Cost and gradient calculation
### START CODE HERE ###
grads, cost = propagate(w, b, X, Y)
### END CODE HERE ###
# Retrieve derivatives from grads(获取导数)
dw = grads["dw"]
db = grads["db"]
# update rule (更新 参数)
### START CODE HERE ###
w = w - learning_rate * dw # need to broadcast
b = b - learning_rate * db
### END CODE HERE ###
# Record the costs (每一百次记录一次 cost)
if i % 100 == 0:
costs.append(cost)
# Print the cost every 100 training examples (如果需要打印则每一百次打印一次)
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" % (i, cost))
# 记录 迭代好的参数 (w, b)
params = {"w": w,
"b": b}
# 记录当前导数(dw, db), 以便下次继续迭代
grads = {"dw": dw,
"db": db}
return params, grads, costs
params, grads, costs = optimize(w, b, X, Y, num_iterations= 200, learning_rate = 0.009, print_cost = True)
print ("w = " + str(params["w"]))
print ("b = " + str(params["b"]))
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
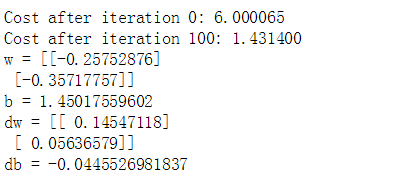
Exercise: 前面的函数 将输出学习好的参数 (w, b), 我们可以使用w和b来预测数据集 x 的标签,实现 predict() 函数。计算预测有两个步骤:
- 计算 Y_hat = A = sigmod(w.T X + b)
- 转换 a 为 0 (如果 activation <= 0.5) 或者 1 (如果activation > 0.5),存储预测值在 向量Y_prediction中。如果你想,你可以在for循环中使用 if/else(尽管有方法将其向量化)
# GRADED FUNCTION: predict
def predict(w, b, X):
'''
Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Returns:
Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
'''
m = X.shape[1]
Y_prediction = np.zeros((1, m))
w = w.reshape(X.shape[0], 1)
# Compute vector "A" predicting the probabilities of a cat being present in the picture
### START CODE HERE ### (≈ 1 line of code)
A = sigmoid(np.dot(w.T, X) + b)
### END CODE HERE ###
for i in range(A.shape[1]):
# Convert probabilities a[0,i] to actual predictions p[0,i]
### START CODE HERE ### (≈ 4 lines of code)
Y_prediction[0, i] = 1 if A[0, i] > 0.5 else 0
### END CODE HERE ###
assert(Y_prediction.shape == (1, m))
return Y_prediction
print("predictions = " + str(predict(w, b, X)))
Expected Output:
What to remember: You've implemented several functions that:
- 初始化参数 (w, b)
- 迭代优化 损失值 以学习参数(w,b) :
- 计算 代价值 和 他的梯度
- 用梯度下降算法更新参数
- 使用学习好的(w, b)来进行预测给定的 样本集标签
5 - 合并所有函数在一个model()里
你将看到如何通过将所有构建(在前面部分中实现的功能)按照正确的顺序组合在一起来构建整个模型。
Exercise: Implement the model function. Use the following notation:
- Y_prediction :你在测试集上进行预测
- Y_prediction_train:你在训练集上的预测
- w, costs, grads :optimize()的输出
# GRADED FUNCTION: model
def model(X_train, Y_train, X_test, Y_test, num_iterations=2000, learning_rate=0.5, print_cost=False):
"""
Builds the logistic regression model by calling the function you've implemented previously
Arguments:
X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
print_cost -- Set to true to print the cost every 100 iterations
Returns:
d -- dictionary containing information about the model.
"""
### START CODE HERE ###
# initialize parameters with zeros (初始化参数(w, b))
w, b = initialize_with_zeros(X_train.shape[0]) # num_px*num_px*3
# Gradient descent (前向传播和后向传播 同时 梯度下降更新参数)
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
# Retrieve parameters w and b from dictionary "parameters"(获取参数w, b)
w = parameters["w"]
b = parameters["b"]
# Predict test/train set examples (使用测试集和训练集进行预测)
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
### END CODE HERE ###
# Print train/test Errors (训练/测试误差: (100 - mean(abs(Y_hat - Y))*100 )
print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
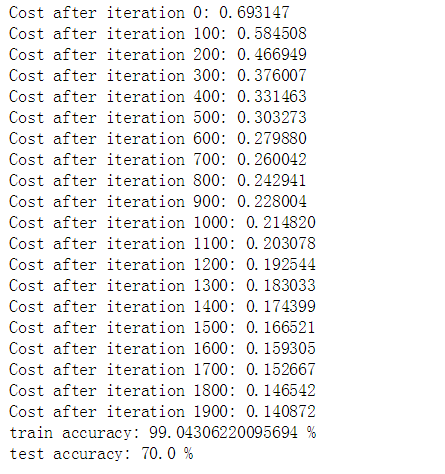

Comment: 训练集准确率接近 100%. 这是一个很好的检查:你的模型能够工作,并且有足够能力去拟合训练数据。 鉴于我们使用的小数据集和逻辑回归是一个线性分类器,测试误差 是 68%,这对这样简单的模型来说还不坏。
此为,你还可以看到,该模型显然对培训数据进行了过渡拟合。在这个专门化后面,你将学习如何减少过渡拟合。例如通过使用 正则化。使用下面的代码(更改索引变量),你可以查看测试集上图片的预测。
# Example of a picture that was wrongly classified.
index = 5
plt.imshow(test_set_x[:,index].reshape((num_px, num_px, 3)))
# test_set_y[0, index]:测试集里标签; classes[int(d["Y_Prediction_test"][0, index])]:预测值
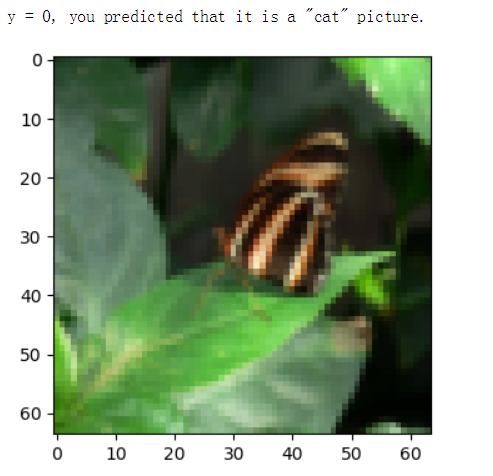
print ("y = " + str(test_set_y[0, index]) + ", you predicted that it is a \"" +
classes[int(d["Y_prediction_test"][0, index])].decode("utf-8") + "\" picture.")

精确性不是很高。。。
# Plot learning curve (with costs)
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()
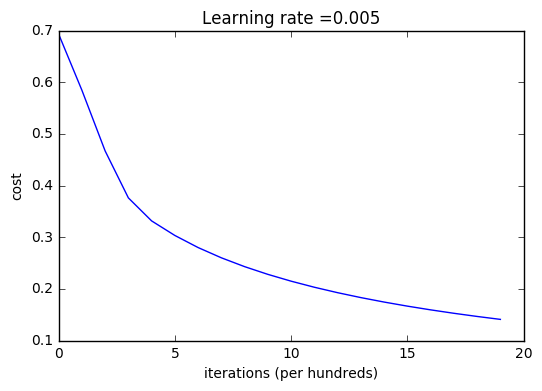
Interpretation: 你可以看见成本在下降。这表明参数正则学习中。但是你可以看到,你可以在训练集对模型进行更多的培训。尝试增加以上代码中的迭代次数,并重新运行代码。你会看见,训练集的准确性会提高,但是测试集的精度会下降。这就是过渡拟合。
6 - Further analysis
检查 learning rate α.的可能选择
选择一个learning rate α
Reminder:为了让梯度下降能够工作,你必须明智的选择learning rate α。α决定了我们更新参数的速度。如果学习率太高,我们可能会”超过”最优值。同样,如果他太小,我们将需要太多的迭代来收敛到最佳值。这就是为什么使用良好α至关重要。
让我们比较我们的模型的α与几种选择的α。
learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
print ("learning rate is: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
print ('\n' + "-------------------------------------------------------" + '\n')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations')
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()
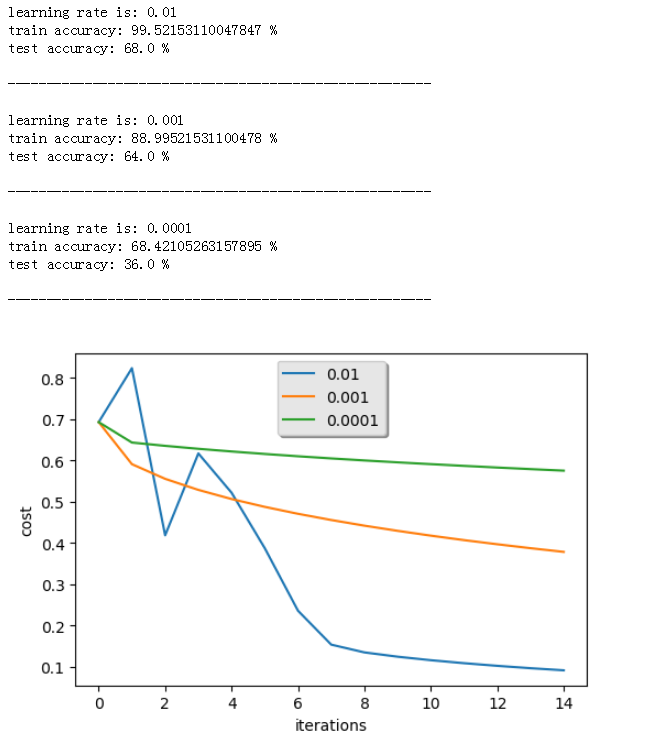
Interpretation:
- 不同α带来不同的cost,因此不同预测结果
- 如果学习率太高(0.01),cost可能上下波。(尽管本例中0.01还行)
- 更低的成本不意味着一个更好的模型。你需要检查一下是否可能过拟合。当训练精度远远高于测试精度时,就会过拟合!
- 在深度学习中,我们推荐
- 选择能够更好最小化代价的 learning rate
- 如果模型过拟合,选择其他技术减少过拟合,后面会讲!
7 - Test with your own image
你可以使用 你的图片 来测试 你的模型的输出。.做这些:
## START CODE HERE ## (PUT YOUR IMAGE NAME)
my_image = "my_image4.jpg" # 修改你图像的名字
## END CODE HERE ##
# We preprocess the image to fit your algorithm.
fname = "images/" + my_image # 图片位置
image = np.array(ndimage.imread(fname, flatten=False)) # 读入图片为矩阵
my_image = scipy.misc.imresize(image, size=(num_px, num_px)).reshape((1, num_px * num_px * 3)).T # 转置图片为 (num_px*num_px*3, 1)向量
my_predicted_image = predict(d["w"], d["b"], my_image) # 用训练好的参数来预测图像
plt.imshow(image)
print("y = " + str(np.squeeze(my_predicted_image)) + ", your algorithm predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") + "\" picture.")
y = 1.0, your algorithm predicts a "cat" picture.
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAARgAAAFeCAYAAABejwD9AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz%0AAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBo%0AdHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzsvcuvZMmW5vVbZrb3dvdzTpx4ZETm%0Azcx7u15XCDFqMQC1hJhQCPEPgBjQjJBghHoAqlKL7kmrEUKlHpVgiJBAPUEtMWipERLQoouSurvo%0ArnfdqvvMV2Q8zsNf+2Fmi4GZbd/uxyNuRGbEzRt1z5I8PM727dtt2zZbtta3vrVMVJVbuZVbuZW3%0AIeabbsCt3Mqt/OWVWwVzK7dyK29NbhXMrdzKrbw1uVUwt3Irt/LW5FbB3Mqt3Mpbk1sFcyu3citv%0ATW4VzK3cyq28NblVMLdyK7fy1uRWwdzKrdzKW5NbBXMrt3Irb02+UQUjIv+5iPxARFoR+Wci8m99%0Ak+25lVu5lTcr35iCEZH/APh7wN8B/irwj4F/KCLf+abadCu3citvVuSbSnYUkd8F/rmq/meTY38M%0A/ANV/Y2f8l0BPgSWb7eVt3IrtzKRM+AzfQ2l4d5iY14oIlID/zrw3xx89I+Av3bk/AZoJoe+BfzJ%0AW2vgrdzKrbxIPgY+fdWTvxEFA7wHWODxwfHHwAdHzv8N4G8dHvy/f+fvc3q6AAWLYIyBqBAjAKIg%0AIkQmClcl/2fqHU7+r0P6rgjJUMqHs9Iu78EKMUZCSOd7H4jR8/TpU4ahpZnNcM4xm82otMFaizEG%0Aa8143RhvLgRRw41j03ZMxRqLiGBsehfkaNt7F8pN7N3DsetGX+19X1VR1eNtkLj7v5p8/rH+fT0p%0AvXLYjleV8p1jz288Jrtz966tu89e5brTz6bHD3/7TXgKx67xorEhkufD5Lu1vuDGjoiN+38vV2v+%0A6r/x78Freg3flIIpcthjcuQYwN8Ffmvy9xnwyenpgrPTE+C4goHU0WHvwRyZALr7v3mBgoF9JROd%0AIYRACB4A7z0xetp2Q9cL1lqstcznDbU0OOfGYy8TH+NLP5+KMUlpOef22loGVpk8jQ032l8+P5S/%0AjApGJC0Gxz572fdf5drTvjxUMKX/3xQM8bp98CYVzFeVb0rBPAUCN62VR9y0alDVDujK3+NDJj1E%0Ao/uDYto3L5/ON+VFj/Bwch4+7PQwDXVd40NP27bZwgncObmHiqAiYMz43WPK5tjgftHAOjx+bID/%0AIsoxBfMiOVSer9Jv0+u+yKp4ld9+E/LzXjDuG4kiqWoP/DPg1w8++nXgn7zqdSw3lcuhkn4Tiris%0AQi96Tc9xzuGcI8aI956u69i0W7qhZwg+uWtGwAgq3Hh9lbYV+VkN6r9s8jKL7lBep49vn8c36yL9%0AFvA/icg/BX4H+E+B7wD//ateoJi9JlsF42QzE/MeRcz0AefP4o1D+f/588m/SDququP71OSeDtDT%0A01OMhcvLS0SEruvQcIUQ8UOHHzrqusY5N7oVZcUTEeKRsRjzKnvotqARVaiMIMbgQ8AYQySdH/NN%0AvszSOZRjLsk3NUGmz/R123DYXy9yTXXSt69j9R32afnbGDOOiRjjW1cyUwvsRe7YocU/PRbCTczv%0ATco3pmBU9e+LyAPgvyZFhf4A+PdV9Ueveg3R3euYoVgmqzlqRr7eA3+Ri3TMoin+7ziwY3qQ5fMY%0AI8455vP5Kw3sY1jQC3GRW7kV9sdIGas/C4V3KN8oyKuqvw389lf9vmHn402VzGgF5ANhL4qUz39B%0A/x7zGWOMNxRLsWBijOML4ugm1XVN3/dUVUUjFoMS/UDbbvHZjZLg0+dNisCHEPCuvvH7u8GQI1jZ%0AMiltjQfvwovR8l8EeZF18a7Lq0SvII2jAmxPPwvhpoKZAsFvQ77pKNJbFT1QNG/8+i8xSa21qCp9%0A31O7BhGTlGCIBPUQlVB5rBiospmuO8U1lWJ2l9+8lVv5KvKzBJ+LvNMKRo7MtZiXbp0s4fud+fod%0AayaRnxeFepMpmo8LnJ+fE2Pk4uKC7fqCBw8eUFUVNkIYBoL21GIRH6klha+tCFFuKpiyEhUcYVx1%0AbnXNUflFt2DK+JguTADyGqH6NyXvtIIpYkgx7xfJMQXzumOu+LKHoO7h3+n/SlVVVFUFQN/3qCrG%0AmATCZper73sAqqrCOZcGhr3pIk2V2j54+Xr3cCu/OHJorRxa29Px/DblnVYwYhqUGl+0i4DRZMXs%0AWzd+8qX8lt9Tp4cdQ3eiLGw+KcaISRg8EhXVfVxn58cammanVO7dfcjTJ5dcrNc8+7M/47179/nu%0AL/0KbpHcp/VyRSQw2AEqMJUjaI9xdm+AFCZyRBHAGpOiWcYTiAz0GAxqFHHuJnvR28m9To4fGVze%0A5r7SfaZzOnffXzfh0H837MzH6TFAXidacYwLtGtzafeQl5XpszY6+UIB0NlZgcewh9fhzby01W+Z%0Ae3TMEnNx96iSBR2xzqAaQGPGYjwxRgaxRB+wCo1xiCaSpkaIJmF40eSxIn68J4Bov9p9vdMK5udR%0AygOxmb6/WCxwdcXV8xUXXLB6b8WDBw84Oz3dWTPAEAO12sSOVQBBC01Q9vGehPEqsXCA1ICaDO4e%0AC8e+eqjXHLOK9EWOZeQoLC6HSubnV960u/Czju5FKSki5cGZHKkESAomBCVGJTIQhzTejCiSxwyA%0AYlARRDURQt+QvOMKJu7T1d+ElOVwr4/14PMXxMUnUtICHj16xPMvH0NUrDFsupbTruNkseDb3/42%0AXdfx7Plz+uDxMRD9gFiHGAMmPR6TlYYJaRBoXpm0sHUmK9uxVU7luO99DFDe3Xj5zIBEVIsjag7O%0AnJxH5KYqesPP5y3IYb+8Dmbzqhyjr5Lq8Eq/X6xGBAU0K/e0IKUzvPcpsgT4voeoGNfkxUkRY7BV%0AlUaThjy83wyO9Y4rmJ8/OeQfNE3D+fk5lXUYEeq6TpZLxmAG7xliSDwZgciAEUU1nS8iIAYRCyIY%0A2YWhy/+SaZx+/2gC5YSQOH5LhPgSUtax+0qyUzIvnQY3rJjXUTSvm+Dx1eWYe3Rc8b5YDslux/rw%0AbSmYJEW5AypYZ0bXKP2uSZBA3xN9QFSJJqZIJyMqiYhJSkr1Bo3jVsG8MTlkk+RjO9CGl5kvU5av%0AqlLXNd/55V/ie3/yp6yXK0I/MAwDbduiDx8CCa/Zdi1eI6cnimqFuhqLwUgaHCKlDQZTWJiFoawR%0AjXlgHJmcIQ5J4cWCSWSz+kgYTqZqQ+WgP8gOfz5W/KnpsWky6eT6r+UxfUPo9VdxbV4lgfRtikrc%0Af2ai+H5IyiWTO8PQJQtmGAh9DxicsYikYASSAhBqQGME1Yz28bXv6Z1WMMakVxEddcBN1+FQXsjM%0AnSgPPThfVZEDC6GEsKfRpGIpqGoiz3nPYrFg6HqGtmO73WIU7t69m/KWMrX/6vKKMHjuP3iI1UDf%0AblJuU22om4b54oS+97RtmwHFauTPFBeMeJObI+ZmUt40srC/Ak/BSh0Vl7VVDsHvUMVCM5d8rITq%0Ax2PswqRyBKp50fN5U/rlVRjPxyItU2LllGl9mLqwFwKenOO9vxEifh0LwHs/0hKKRXUs3UFE0LBr%0ArzWCsw7Es90Gri8v0m+HZCHbEAjo6L47l1xxKfQINXtpN68yj36avNMK5vAhH/qNX03ibnLBZKKN%0A4Yn8vj9jXvYQrHPcuXeXYRj4wRdfcH19zaxuCCj379/n7r27eI2YytFef8HFl0+ZzWY8ePAA1Ujo%0ANvQ6MG8si8ZRuYoYI5shYyuFsRkZoyZ7dxQn61Eyh5JmzquVjB9N7jtnh2thLPthct/5d02ZbCYr%0AEEVDGZQGkbhz3Y48mxc9L/MSXC3/Ymnx0XNijKMbOCr+I3SCY9SDN8WZuUldeHU5hgW9yHWzMTCr%0AKiCyXW9ou46+3TIMA912PSljEpEIJj+j4HusFQIOFGwURBSJqVdDMU5z/7yu21jk3VYwZue5AJNY%0A5oEyeA37/HC1G1dB2Hs/HJjl3GOrZUkdmM/nzOdz4uDx3nNxcYH3HhVwTc3i5IRG77LZbCAKfd+P%0Ahar84Gm3hqquqaoKY5RKiqUURwV4uKqm96mZp2OnieqoQPKJYwRhl/pQBvt+jR3YYTlJ4dx0zX7a%0AJDucQK8qO2uzHNi/vZcpksPrvA0S3iEm83Wuc+zv6fHaRDT2hBBoNyva7Zpu20IMGCUxxcOQSHbq%0AEElFzaa5cfsKlr33ryvvtIL5Wcqxh/uqq96u+NSc+/fvs12t0wrTdUm5zBtmsxmz+ZzTeo7GyDAM%0AbDcbmqZhfjJDY6Rt18Q44Nw8VcczdXLDYkh+84T7kST/P+4DkIruJuLUjRBQczio83ssJL+YrZOX%0Ag5rTEHaMEcwxhnJxsWTXVuBo6Ps15JCYeOyzFymAN6lwji1Cr/t92Fe+h66LkUjXdvRdx/r6kq7r%0AwA9YUkBBJBKGhMdEBZwdU1JijJNl4fgi8XXlnVYwb2MFmg68vYF68H7MtH7RZIsxYoyhqhKOMQwD%0A2+2W7XbLfD7n7O45CoQYaZxjUZ/SmY7V+poweCBgnVCJodeOugrUdc1MKqJGhuhzdb0w+v4i04pm%0ATemwSULofikHTTcPrpxhx++MwLKSI1spyuAneJRIzJEuQEtqRRgtoKA3FcyYtClmhNRT6PQlLtL0%0AuUgevgcWTAhhF4Fj34L6aZbFYYLgV5EXWbhf9ToFizk8rqpcXz1nvVrRdR1+u0VEcAgx9Fw8eU7f%0AtfTbNrXHnHB27y7NfIZdzNIYsaDZjRIBm/G1KdT4dQiEf7kUzM8AwP8qFsy275AY6fueq6srrq6v%0AGNqOtm0JITAMA1Vdc+fOHUzbZhfIsG3XeN+z3ixpmgrXzAkhMgwdIkrj7txoxzGXTSZ/T+WGFfIC%0AJTle58akDaDTdIliCcVXcksPJ+HXnZAv+51jv/uidnzTMgWUj03s6bG2bRmGAfVDKp9qDHHoGYaB%0Ay4vnbFdruq7DIMzmkfnJAlu5veukBWNfGR+6lb+QCqYXpZHpKnoTrEtWx8ujCNMVQfa+m86J++o8%0Afca00yXRnVT3VL/Jf5+aE3rfM6uUX/orv8rFxQXXF5d0fUvfdvz5H/8pFuHBgwd89OghH3/8MbPZ%0AnG81H3G9vOTJk8eEWpm7E6x1dEMkOE+oL3K9mRStCt6jxoDZpRqoKho8ELGGkXQXJCTXRQ0YQUgp%0ADhILuO2SRaKCqGBMnVY8qfLdKbbK91/C35LwHtXCJC30L4hD2AddARt2SilZXPnKcjMaN1WWqtm8%0Aj9v8vWRt+RiJObQ+DIpIjbWWoIoYn0KvY5TMImIzucwAyUVM1wopIpfvUzVHlWSHRWV9OvbbVKbt%0A3o2bXbrKdNJOUxjGBUKTdeGcpv6LASRiQspd67YrtusNzy+eUuq5V9ZyMp/Rr7c8/fxLNqsVzz79%0AnOgHDOBVYd7jz8+oT+fEqqK3hpoGFwUXBTXCICEnCqdgQLmD8IsI8h5zkY4qmNdQvm86miAi9MGP%0AA8k5R1VVqV7M0CXTNCpD8FxfX1OhnJ+fY8wZs1nDyeKM5eyKzWbFdrtlsZiPYcyh64mVSziM9wQf%0AwFow+2Z+Yf6GEbiNRAlZoVqiCpIxE2vyBDQCGhDNq50KBocZc4qUOLpCBW/ZcYVED1ZAMl9D2bmb%0AebKOvJxYLKmM8RRlnRX/TuPrHoVH9yr35bBtrs2jmqsaHiwyWtLtNbkGqa02v08rDaV73f3G4co+%0AveZNzOTws1c7nqJvuYWoeiTkNsTAZrVmvV7Tti0NlsVsxryZURnD5WbD06dP6duWtt0k1m7+nSgt%0Afd/ThHCg1NhF2Q6oHl/XXXynFcyhHFMub+I6ryN7UZx8DWttshaCptq7qgQifdvhfT/uCqAxAXLP%0Anjylb7fcu3+X+XzOd3/111gul3zvz/+UunZ88MEHbNcttWuRVtDspjjnCH0ylYuFVX4fQE1ASaFp%0A1Kf2ic34h0Ml085FEJstGrGgBsuAiMVSjfdotNkLX+5IfmYyQPPWKuLTfJ5Yi2YyiEfMSCGo3cOQ%0AyrVGfkpWOGISrT2EMhGVKCav+hHEI6ZUNJxatyXylTClnXKJo4KLewpst1FFCGVRK1aWv+FGHFUw%0ATO91dzRGxZhi/WVWtk/17ZPajmj0SAxs1itWq2uW15fU1vHhw/cJ2y1nZ2eslkt+/w//hPX1kuWz%0AZ2hIfWWM5u17Er+mpA2Uvg0hICrJus18KWWny190P68q77SCOQY+HfqPr6sk0uAr39u9Hznzpe3a%0AWwGsYgJjuQZr07v3fSrl4AMxDATnaK1luVxiDDSzOk+qwGKx4PT0lIuLC1arFXVdE9hZKmlyCjEM%0AicuQzVtVzWBoNrc1m9sx5KzzNKEQTZMtIa2JISqWHQU9Zrdp1+/J8plO3DhOkrEvct6WkX2cKBYO%0AjuyYxYXEaCRZHLJjTqZraVGO+ziTFsUlycWLKEhMv51zx8o55dkVi3IHex9iV4fuc1Zgh0TGrDhF%0AJu7XTwEDpxbQMSvcZeMpRo/GSBx6UGW1vGK5XKI+UNUzZk1FBFbLax5/9jlPH3+Jy/t1pb4t141J%0AyRiZVF880n97SvXN4GLvtIIpE7bIMeVSHvxXka9jwezwAqX3AyKpHMPp6UkKz0rk+vkz4uAZtMcg%0AOGNp2w1/+Ic/oa5rPvr4Q+7du8e3v/0Ry6XhV3/lu2w2G/7oj/6IGCMff3DGbDajcRXRe9pum1OA%0A0n1bKczS7Oe7MrBTkqiGnFcklrQrjME1BsFiKTiOydcKGDU4rUeFYHS/nOjOvp7sM2VcVkb7VsgO%0Ab2C0XMqzHHS/XEV5jj74PTwGa1PIPfqsdFJbvQ+J32MNSEryS3V2ym9qxhcM2LIp3fgAE1lQZHQb%0ApiC4xIhO7jnG3T5a5f1YGUpjdlNtb4zEpAin33OSXOpus6Hve9ara9QH+nZLFSPvvfces9kM3w1c%0APnnM48ePGdqOjz78gG67IWy3GI3EQVEfgFT4fgiBruvGOkTGGDS+WMEcAr1fRd5pBXNowZT/T3OB%0Apu9TOTxWHu7O7d+tLKXG6fT4YX0RKcenLkBuU13XdF0LKFVTU9dujBQ1s4p+u6Gua4ZuS9cPNFWF%0AEeHy2QWrq2u2qzV3797lzskplal4eP8hm82G6+sVRuH0/oIYI32X9mJypvRFbr9PuUhkRWMsYDQz%0ANiMiijUVxggGwdr0ijFiTdksLmZjYCBxVgzokCdHcYUgeCUlRGbLKmM2VQZ/u6Hb9V3uH5cnn+bU%0Ag8pZyNkwsjfR4y6MrAoqhBCIfUcEnKuxJoO6qkTfUecN8hBL8B5rKyARDK2RHQ4kZScAxUlNIS+O%0AC0VM34nej25nsoDC3hiMIVl64xgo1eUmSreQImO+jgYPIpj8vRAScW7oW4LvqQC1hrN758zqhrqq%0A8H7g8aefsrm+wnc9QmS7XjG0HUZj5lJ1KR8pu0tq3ajIpspjanEVF6n8/xc6ivRWZDTL2a1qWlga%0AB8dfUbwGbF0RB4/6gaZpuHPnDs7AarNl8B1Dt4Wo1LmynUiePDGyXC7x3nN6esqdO3f4lV/5Naqq%0A4rNP/5TVasXVVQpjG2NQH8ZdJjW7Vz6mCIZxacBbJ5gqbRJnMgZjJSkXwy63Kf0/VSNKylRJHBVJ%0Ak0SHMfGyuELVmC9TBmY2x2My8wkt5Bo4o6KJbs8ajZ69iTC6ZLHfpUUAEiwSAsEPRBQTPSoWl90A%0AocJYQUPAi6JDQHPiJypgPUZyBcGMSaEGCZsbTk4IIdHtc9kD0ZKxvD1EetFodwtR/sy6+XiKTN4N%0AdjeRdUBjZLu+wvsE+od+4PTkhFndcDKb45zj888+4/LZUz799FOMRvo+9Wnfdmy3a3Tw+VnqqLBi%0AjDh7ymw24+TkZLd1zqQWW2r+iBaNf0/fX1duFczPQFQSZVtFx1WraUqZTJhVNV3siBqJPmBcjuLE%0AjOpHCENgebXEioX3wBnH/QcPcVXF9dUVIQTms5rAMPrZKQ1AxzB7yhOKaWK6Ag7nSYylRE8SDlX2%0AbHoJu1MDZHemKB5j9zGNwplTU0oHBFR3kagEoCqqQsyMY7E2uygWMgQtYhKOIzsN70iAbpAcno6R%0A1JQIhXQYPBICeIPEQCIECkTBiGLGLSjK/UYoSmgiMXrMBNcYI18aJnlqmYgYUt+PikRSYupUxusX%0AXElSmkbMlH8RobKCcQbRiGigaze0qrTrFUPfY43BoURjUIXKClrXDNkN1GxtHZIvDzHCsl/Sy1TI%0ArYJ5Y7LjP0xMGHbrTjn+OiUgI2INagRxkgYhjvm84fT0lJX3aHR0w0CIKYxsbXKjRGQkUz17esF2%0A0yFYZrMZjz68w/sffMRm03J1dZVXqTQxVQNt26bM3iqlFDB4jBVMBTWptoyrbJrIpkLFjtm0sWTW%0AYohRsTZN9JhDDCJpVU8GSwKKxygMO5cjWVMRY1NkRONAKeVobfqt4Ie9AVy5NOBtVSHZshEVKomo%0A0XFL3lpM4ndksLYUXxJNESobPG6waAyIhGR9xGp0e4zUoAXXyZaSMeC3Y5bx6OocFszOIXdDyKkX%0AGUeR5JIV93gE9mV/X6zx/xOMp5Au0YFh8Axth3OOO4s5dV1z+fw5VxeXXD6/oOsGKpKb6lC8pjov%0AlbVIVTEMHZvtFo2euq7HdJViuZQ+tOL2LPLSJjNx80ZQ/ivIG98URUT+tojoweuLyeeSz/lMRLYi%0A8n+KyL/2ptvxcyVm4u/mQRtC4PT0lJOTkzGVoCQ2QsrTKS6SqhIDaRvazYaLiwueP3/OxfUVq23L%0AnfO73Lt3j2EI9EPIq5bDmirhJ4X+HRO9P12XTEojkfMoq5ylWDG7/ycAdRp+HicHWeVKypgOGtMr%0AptfgPT4EBt8z+J4QPVFTuPzwhShiQGPIK3t6CYrGkBSiNRhJ58QwIMFjNKbEPk1Wg0UxpPCsEbAZ%0AnJUYMaSXFcWiEDzqA+oTG5bgx99Pbl9qg8aw167ytxCzJZdeie8TMaJYA5UzVC7xi8qrfEejJ4Yh%0ARRB9P+78uV2v6NstJ7M598/vsjiZUTtD3yaAtm1bus0akaRQZrMZ8/l8pCMMQ5fcccKekjDGMJ/P%0AWSwW4+IFL8dXvk4ECd6eBfOHwL8z+Xu63P+XwN8A/hPgz4C/CfzvIvKvqOrydX7EqGCOUdJHHCW9%0AD8eqqb2gT3ehvZ0FI2Ooc78eCEx81BzeTdGSFKpNBcSVyswTnRuLWkNUh5iKs4ffYjtA1VyAD8zt%0ACfiBqqoYYuDi8hLvt6hANWtYqEe2K3qJzBYL3JeR9fWa08Wck9kZw6ZjtVrS1I7aGeand4gxstou%0ACV6JKlRS4VydgMjoCOqQaMeVNgy5FklOihPAmQrRAgamiE+MkToEHAUfGfYq51lrk/XUdVkZdZOo%0ASTrHubRKSgbRx8lgI0EFCS4p3SrxbepqhgB+GLAxolUCjCOZpUuyLAxQ2/Tc1HssYHyyKmz0CaBF%0AUb9JygASWIsgUbAKOuQN9KqKYRjwvt+NEZ1YMiN3JgP+3mCMw4hDFJxEJApbsxzHS/QeYqSyFcvN%0AGmscYIi9Jw4D5yf3aZqGB3fvEWPk888+Y7Na8/knn3J9eUVlLQahX7VUjSN4j48DYQjEUmQKpXYV%0Ag3aoH7DWEOZz5md3uLM4ww5CDKCV4gWiy+M8JktITZV7M88G82Il9DJ5WwrGq+oXhwclPZX/Avg7%0Aqvq/5mN/HXgM/EfA/3DsYiLSMGbsAXD2xlv8FuRFHILi75YSDsYYfBxSBKTsL61x3LytG3pCmyJE%0AtkqlH4Zh4KJWFrM5VuBkvuDu3bsYI2zWS7owYO0sRaqaJpHwQsA5h3VujIIUZXAYkZu2FXaRuek9%0AFTN7CkgXaywpnYj3uTr9XsWIm8WMpscSQGv2zPOpmb7bTXNaBGoa5duPMBbXpfy/RNgK30U1adJD%0AK3MvnD5peyEMpsaktdNkrCr9ZKIBmLHQ136Vw3L97bZLqQw+4P2A93FUuuV5rVYrwuBpmiYlNHqP%0ATFyq6+vNXtuMMcxmM4a243q9ou87TmbzVLmubI1zMA7fprwtBfNdEfmMRK74XeA3VfX7wC8DHwD/%0AqJyoqp2I/F/AX+MFCgb4DeBvHR6MHK/0eriV6s9SpuG/6fux80r5hh86y7ZtGRBqoA9pUjbZX16c%0AnhBCoPMDYfB8+cVjgkYunziapuGDRw+5f/8+3/n4Qx49esTTJ0rbbui6NIBdU+GoxgFYXlVVJYp5%0AVSEusY1d4b1MI0qQuCWT+ygDvNQVKVjL4QQtvn8x10sVvEPwcUoAi1KsxoIDpKzsEAdiYPwtHaZK%0Aate2xI41exhIZfapBYUwV/KMNBvZMZZatZEYlDYk9mshAeqBsrNZsY0pFpJQeSXkxNQBMAw1DMOQ%0AavyYCmMcwzCw2WzwQxonJydnqcQChounz/jh1fcRYHW9ZLvdsry6TjwWEcLgE+1fJv2YS20YBGsM%0A56fnDMMs410V9ekJTdMkNjkk/3Gv5/KzhRv1mn+eQN7fBf5jkvvzPskF+icZZ/kgn/P44DuPgb/y%0Akmv+XeC3Jn+fAZ+8kda+BTlULjdcq/yq5zMMwr179/D9wLBtU724PIjHARvTRJ2J0Plcz1eV9bpj%0AGAZWi+R/X5zMMUY4Ozujrh0Xl8+IQxz97bK5WymXOMV9yr5PU1/2cOU+VDAiU8AyoFp2FZgS1Exy%0AVcqCP3GjirVTrj9yXCRf3zBRQtmiIe5ZMmOfvuRZiEiKABVgVhMXRWKOSumk8JbkPohJ5aQUjzhO%0AuJFkF/L5Oc3jUFK/lHfBa6HlG5y1BJ8q0G3WGyrXMF8sWMzm9H3PZrtJCuX6GlXl+vKKbrMdlfng%0AfSq/OgzMapfTImS8B9WIhtL/Nue/NVjnMJXbjatjFiuvzcJ4qbxxBaOq/3Dy5++LyO8AfwH8deD/%0ALacdfO2l96WqHckaSicX/EM4WhXgAIJ5sz32U+SYBXOj0r8RFEmrmxE+/OgjnHP8+Z99D0eKGgGj%0Ai4QxxAze1mJx8xMiynr5lL7taO+cUTvHl19+yWaz5v0PHmKcpaqqZDFYg3WO+WKRlAqJ/Ded4GMC%0AYQ6Nay50XloefdhTfFibFYeIcKa1AAAgAElEQVTuHS/1aIsUa8NVOytlCjpOw6bFPVSUMTyelZgx%0AKQ/Ie48PfZ4kU77MhMhmJsp50v7dcylqMBHjUrt2qtV3O0yoKJIyecc654cruk4r+Nsx7F+Ac9+n%0A33bGEIbkOlqxPHzwHov5KcY4rq6WrFYrLpfXVFUqi3p1cUm73lBVFZ33KTM6t7mpaoahwxmbI1XF%0AkjFEH+na1Pf17ISqWaA2VUTEWWxdocbip+VUp7dzw4I5ctIryFsPU6vqWkR+H/gu8A/y4Q+Azyen%0APeKmVfPOyqFbdGwPbUgunDOGxdkpJ+t1Aka7fodb5AligKHv2U5qxQxDqlrWDwMhm97b7ZaqcqzX%0Aa6rKYqzNtXX3MYk4wRvSAf2pBdN3uEecuB/7BbKBPddkzwpjd/1jv7EfEtW94tNpX6bdDoW7vbpv%0A3tvhbx5iKYfWxg18hcR5EZHEBh53R8zV9w6mY/b4iGMSZKpFbESx1o2JrI1zeO/pty1976mrGd96%0A9D7GOOpqxna7ZbNc4fueJmNspbi7MYah60eCoohgJRMlje4Ui+ZtlGMC5hcLyxACUYXBR2yKzac+%0AMDss6m3KW1cwGaD9V4F/DPwA+AL4deD38uc18G8D/9XrXnu6GuZrAa/GPjz8zjj5JlyOl13jRd+H%0AabV9yRteuXGboLGNRhCba+2GAVM5FmenVPXAYpGo/8MwjKv6fD7nZDZPoG/XYazD1nNOFotUJhFo%0AmhTxKFGE+ekJIkI1s3sukpnkEZXBOXXNEr/FjnyJYoWUGsEiksp9VtOQdVrhffCJISpCCDtavbLL%0A7C7PrADE5djozmQzwfueEISqaohE2rbbzwY2iayYrCZGi+2YUqvEpNKiISYrTRMzl1xutLBe+74n%0A6jA+w2IdGE00gWqxwCCsVqsUFjb5fmJRZkKM0NRzYk41qOsK7xXfB6JXHtx7j8ViQVMvqOuaZ88u%0AuLpcsrxasdlsWPappOp2vUnfz/ykuq4TtdBGYlVjgKqpkaj4YWCWd37wPrL1HR4IIpye3+P+e+9x%0A8p1v4+YN1WKWiAE5kJD6KEKM445Xr8Pyepm8cQUjIv8d8L8BPyZZJn8TuAP8j6qqIvL3gN8Uke8B%0A3wN+E9gA//Nr/5iZZP8Wu5fXc5EOgdgXvb+qHFsRp3IDn5Hkrvj5DNfU1Dm/hjwZi6VSSFgikjZx%0AQ7BVcqOqylI19U6BVG7M2E5Ro51VISJjfxRlYTPImtyk468y+Mr/RW9aL7CzYPZA22z1HGI4h+eM%0A4KmAaiDmQlYhDBnk9TcWlXKtoqhEBD/cLHs5/a1xy949y2Z3bomIEZWQPbUYUsTM9ym5se+Tm2ar%0AkmqwYwSr7o8f7z2X16sxovfw4UOaesZ6veXi4oIffP9HPHv2jOfPL/He04ZuBNCdGGydd2H0IbGc%0AYdw3vZ41+H5IXB9rsWrw2iPGJKUnCq4iGjtG/WKMBJPry7i8a+jx4fy15W1YMB8D/wvwHvCEhLv8%0Am6r6o/z5fwvMgd8G7pFA4X9XX5MDA9xYqb6qTAfDFBMof5fV7HWvV66TaqTddJXUCEYsJ6eniAjz%0AkwXaXfPFF1+w2WxGvsi8bnA56VBjTGzM2YwQNxhjePjoIYvFAowyn8+SUrGCrRyuqjB1Xpe0gF1K%0ADCkkmtwAHRPiDnGSsq/ToYsEEPp2fAa7F6MrU/otpQC4vb4B9qyRfRB8NzHTedWIZSn7SabT6+12%0AYOgpkaXxurrjryRXInGWrJi8MEWiRjTEbM2kv0OISAxst1tiTkAE6HKd22p2khS5rcZSHHVdE3xE%0A1Y8u0nc++pi6ntE0Devlmk+e/4Sf/PhTnj274OnT5wx9yOcaBtJC4jKu5L1PrvR8DjHxaIqyan2H%0Ac4mhW+GIISRrTQ1X2yVqHGZxgpnNqU/mxLwoW2tRMWNdZSWD3Uz+PjKmX1feBsj7H/6UzxX42/n1%0AcyGHq+H0/U1YMLsVNz/EyYMUEYxLeElA6XIx8PV6TZep/rOqZjGb8/7Dh6NVM3Q91WwfX9AYWWQg%0AF7OzUMbaJ5qNF9WcHBhzEEX3JmBpc3GPiuVU7mcKxpZzj7kl5TtTZTPt56n1Ur6vqohVUDtRdJKt%0AjnJdQA6xlXjDupluteI016nRVOApaqn0NnlWIaI+MMS0+2aMEYmawsITJWvYv0/YkQudS9SBZbcG%0AIk3TcHZ2zr077+G9Z7PZ8L0//TMuLi7YbFqGbkhKzgkxKD70DCYVDZtVaZvh2lVUmbhI1F31q6jM%0ATxYQIrV1xK3HB2WzbWmHnm4IVFXF3XsPOL9/j/Pz8xQGN4aQs8U12y4/TcGgPycK5mcpURircDGZ%0AACV/rby/zPw7dIXiZFCOJvtryiGYuDPPUzJeyHTzUqm/nOu9H3ceKNZTbR1XF5c8HZ6wur7m0aNH%0AnJ2c0nUdp+d3OD09ZValvZI++PB95vMZQQIYpZ41CbPxydKwGQdJC7bicy2QsqIjktMHC3FOx3Bo%0AWYkLRqUK2CP9l/uruGtTAt7U0gHGsGtx38adC1VRPCHsIkg7AHUCIJudAo2RzDnhxjNLClQmFlUc%0AeTmFLRWCH4HyQduR1BaHHScpxsjQ9eMWNLCrSVRV1RgO7vue+/fvc3JyytnZGarCD3/4Q5bLJU+f%0APuWzzz7PbrBjPp9n7Kin6xLb2UePE8O6TwtJyPd19/QOTdNwMp9TInbbdcv2eoXB0l2v8H2gmc3Z%0A+p6tH3CnJ9x//yEP3nuP6uwEsdk9NJoqGB7RG6K8kOn+uvJOK5jKWGw2dcsKDjuFUtibaqeWxFiN%0AGmUXeh01d2gmeEUqcXsYiVDVsZjTzmLJE0c1kdXz4RRd8BRClylYhkxIbCqIqQhqaBGqkzNoB7r1%0Alnkz4/z8POWgDC3LzZL52QJvIpvaI9XAnfsLZmenuLM566HlzuI0F3EyaAjYvHKPPAlSuDUyZb2W%0ATzRhWxEGP+BjKgLd55oyKXKRXRpN7lNRPglINnnC+6yICh3SHPTXzaLeo6XVl1q9mciWgdiScSLk%0AGjXag9qkpNkBtTEMlFq7IonF63VIWQ43FGIG49US1NINmurJRMvQblkur2jqOoe1LX4QjNQ09g7B%0AK8HVBFXO7twHoAsGbZT5vUdUVcNy1eO7nk8+v2S5XHJ5uaIdLCKpvGk/bNBsKbbbTVJioWcTwojz%0AjHlGJkV/ukzEXK/XbNplqgcTU8EyxLBaXxGAvnZwUlGdnxJOas44S2UmSJn0lDEAqayEWGKmB8x8%0ACXqkPnXhiCZ6BXmnFczhpH8VmZr6qYbsvk/vYubBMVVKO7OxWDiB/cjR18GCpr/hXIomhRDYXF+x%0AWq24s8g7QmoFIjSLOef372FPNJvldpz4JycnmUPhR1JYWdkNu/sspS738mpExoJKBR+ZYiOH2EeM%0AaRIU9muJVO3clqkSfrVo3PTcfRdoB46P/KDxc0a8aLQ6J0BrUv7Hi5BNr1vaX9sF23aD5hKTQ65l%0Am7LAM3he11SNpTo/y9hPSiz91ne+zcnZGVfPLtgstzz/8hmb5YqLi4uUpNil7Wr6vuf64hJVZdY0%0AI/ZnrcXV86MuZ9u2bLdbgDH94+zsDJ2ne15frthu10RbYWc13/roQx5++BHz+XyM7KnJBLvC4p1w%0AtKacsmL9KxCNEL4iCvyXQsH8NNkNIsYVu3x/V6h6d+6hsthTSgdRoMPzvu49pG1mHbNZnchwPoAR%0A6qrGuJSOVYDWuk4r+SxXlTcWaptqzBS8Yg//GIlfu3q9+xORPSr84eQ/vL/DvJapQjmcyIfvL+qL%0Aw2tMLZvyO6O7dfDdaaTosH+NOd6m6YbyY17WZDKViV/VNQZLXc9pqhlNk3LIqlmiFNy7/x5N0xB8%0ApN92XDy/Yr3csLxes1mtRzyrbduxgFiMiWU9ZtFLsv7E7I/D6eJTpHxvCC0iqd3zkwViHEEEXMX5%0AnXs8ePCAZr7AiiVKsu5VdsxWHdMFDiy7HH7fQQ9fTcO80wpmur/uyxXNoXKZrlrpjHEFm37rAPQq%0AFoxIMvq/rgUznUDjpLGM2Ml7jx6wXW8Ivmc2a3jw6CGqEVdXGGe4cyflrpydnFLVFkIkSMBm9DLk%0AHR9LNCZOLJiyKbro/oQr4efStzuexL4lAwkz2m63OOeYzWZAWlmLBbQ/SbjxrKZ9NlVWRbkdRq+K%0A61ra43IoXpU93lDaCWGXnpCU0n4u1TFLptRLiTKgCGIc9XyRyY0JUzo5PcWKo/cD1lo+fvRRiuYM%0AA35IgPhnn33JT370CaurNdfPL9ksVzx++uX4G/P5PPVTM0uLRT5uSMqz7bejO1r6tril06jmdrtl%0ACB7NBeWrqmFRzajmC0zd8Mu/9l3e//ZHzJp5qlqjyYIREeJhdnS2ZELpj+TH75TMz1k29c9EXt+C%0A2a94Xz7b1UIRwI/nj5hE+jV2iurNWjBTGWJAjEm1e+czQgisr1u6nHJf5eTEZp6sFuccPvR0nSa+%0AQ/RYMyPGFHEo4efxDsrvZWVbTOTd8Zv3NI34HMo0rD29p0OLb3f5nZIpymLflbqpeMvqPxbDygrQ%0Aje2WvbaU+3hpNb4DKfdpjEmlCmwGlJ1FbOIWjTVxxGDEUNUNqtB1PU+fXyS30gvPn1/w7OkFy6sl%0Ay+fXDF2391tFeYfMqdGsPF3Opg/qR65OCIHNZoOqjiBwqojYJGXYJ5Q+bdubInsqMD9Z8N7Dhyzm%0Aqd6QszYhWFIggONiyLD3keDJV5F3WsGMxDGOT+4pM7VI8aFHpcKOWaoxkZWS5QJkMzwVjZZMXkr1%0ATGTS6WUCTveGnroZe+HTI1bP1Ow3TsAYjHUsTueIKNt2ja0sblYzmzfMT09YLBac3z1JZnLbIVEx%0AJZ8m+DEjuERxppOz9IOIjFtZFAZs2aSrRIEOXZTyt/d+5KuU0LmqjjlO5XplcO72E2I3kXOflIzr%0AqRUzjT61bbvDXdiFtfu+z65isp58xo+SVeD2rK9prtFUpm0sbNlePHXTYKxl/XgLJnJ6lkK8TTXP%0A2dCJNf3pJ5+zWq34/MkTrLV89ukXPH9+yep6Rd8OxC5QGYub7SJnhSndVFW6N2NG98w5h4+Gvu/5%0A0Y9+lKyUTBNISaw1p6enbLfblELgIyW1wtUz5ienPHjvEY8+/BbzszNiBnSHkKzjmCvnlL27dSjA%0AeVGyBgv0OUyvqhAiy8uLo/330+SdVjBFjpm7079vSt5gTE3W6KmKPSgqume3wKTsg+5KHL7o+i+z%0Aql6mDIu0Q0/jKirnqOfJhD47O80PX1NdAFJIVqJS145o09awxlT0fYshA56UTOAcwWLCPRFGTscx%0A1+EYFnWIjSSLbl9hvqzvy/fKOVML5lj/HQLLh204bPPL2j4Nk0/PKcdLJMxaS9sn5rBqCvXP53NO%0Az+9grQNviCr0XcfQeaKsubi4GEsxfPrpp3TdQN/2aIB5nbeVMcONflLV5P7k//shuYRXy0v6vme5%0AXBJjHEHa2Wy2t3h57xGTdkkImigGGEM9m+HqBhGbymlpKilalMpY3B1JJUdJLnNSMvmZWKUPJXeq%0AZ/2LqGAOzfPi909XQoCULKd71oqzieJtjEvh3BIyprsxYI2rx0tppvFL3n7jkNw15XYcTijYrRTA%0AWH1sKioRcYmFeyKnOGc5PVkkurwRfAx0Q0sbOlarVHvX5dV9GDpESVvSjnhTZIh+D29RVcg5Ns7Y%0AvfbrZMKVqnSjxTLpkxgjUf0INh66jNOcoKmFN+2PAlpOrZdicR5zpcY+mnw2TjQRUJstomrv3Bub%0ApU0+K5ZUuUYIAbEVs9MTDCecnd9hPp/RVKng02effU7fe2JI2fB+SPf95PkFl5eJ6j+fJ+a1wbCo%0A5hAj3aSeTvk9JW2o5zN25Pth/KyqKr797W+jqmy3qVTDdrtNWdjWjrybqI5IQCP0UTlxjrN795if%0AnhFz2NqZKitPN9avEUm1oY2r0FB2YYDYp7Z0qyu22y2f/uQTHj9+zL/4vX9xo/9eRd5pBaMHUYPp%0AA5wO+EPGKZRVxGLEZYc0r7x5G4vptaZuj7FZoeStQF4UtZi+9lb1PTxIj7Rpl6NTuWSyYyPWNPgY%0AUvg5J/m17Qbve+6cnSWf3SfmpsRkaZXyn6MCOQBavffJJZu2fZIKUNo0nfyH1kRRDlMlX1yVw36c%0AXvNF1sRh+6bu2Yv6mbI3Uf4JYzIgH3eh6alLNlWoU7ZzOScR5rLSix7nLCbXo9l2LWGI1FWyKvzg%0AefbsGT/44Q/wPvLhhx+PtP+85wEaw14EaHzuUbm+vmazXtP3fcqYBu49uJvoCosFIsJsNhtz0fq+%0AZzabjYTMupphfKqDbJsZ9WwOxhKya2REcolUGfOXRndISeBuiJiY8MWuS7uNPv7xj9N9/flf8Pzp%0AMz77wQ9uPINXkXdawZQBOCbt2VK2cD/UKaaEpHcPN62woGPoNk+Spr5hgoc8scQkP1aAWsIYRZla%0AMlMTNsaUgVy4IUWmCudwZY2Z6CbWUuedBXy7Tfc2dESpmc1mRFWGvsUPA4t5Cl+LQtSQa5akZD1V%0AxVtG03hUiNmqs2L2FERpe8FUpjVbpm0v7yV6VKj1q9VqVArW2tEaKTs8FtZrVVXjdcrzG5MM87Mt%0A4OZsNhtdmGlFvl2qQd73aYwIBlRSILZYMCKHaQQTJWt2ZUOdc3gxiCUVFkcJ3jO0a7bbjhhAjE2W%0AZDfw5OmXrFYr7t47p64anjx5TFU1NNWMEJW+3eIk7T1ww4UMMWVoVxWz2YxFLm25OJ3jvWe5XBJC%0AWjTKzgCz2WwvqrRatQwx0MwWnJyeUTV1KkjlPT4GGupdtnoZfwomg/viI3HwrNdrhq7n+9//PtfX%0A1/zkD36PZ18+YbVc4pzjvfni1SfmRN5pBXPMXy8yjXwcWjaoGRUMZlePNrkZ+6ZskcPiSGVD+xfh%0ADocr5c6a2rXvmBTzt6oqRMFPdhYYhiEVCiJN6HktY7W6EAKVdZNrywjC7qyAnZWQuDL7/TNt+6vw%0AYKZgbflesV7Kij210qYKovTfsWdXvjctr3nM4tHJualvJ8qjYGrjgrJfY2f6/6m1pKpE0xBiIIQB%0AyUTM0pa6rgGh61K+0nw+p21b/uKHf0FTzwhB+fDDu9SuwfeB1boDIvV8tme5qSrqA7PZbAR5Cx5W%0AFGsZC4VEWdITClCcynTstiNZnJ3SzGfZesl9Ibtgh81u8lSWyyVD1/H86TOWyyV/9Ad/yPPnzzHL%0AZ/ih4+6dM+Z1w2bb3hysryDvtIJZPt9ipeLk7ikQMLVL0YJMaw4Z7BS2CIZK5lhNGcxp0oGXPkcf%0AlSjQxQUJ8sorrG0Bj2iPRAtxjtAQw5a+T2n43qfcEeuEWd0AQswWQNd1tKvV+MALt2GqrECIomCF%0AmZsxsw21sZlVbFFbYZ3Qrq4IvudsXiOOvFdRzLV3Df2QwqFOsmVgQIxQ53q86dhBse+8najPbN8h%0AR55qlCDQFIuMhD+NAzdEgipt24+JiCEoXTdk/KbaswzK94q7VRRRWV0LcxigVcWr0ua/bU5CPFuc%0AZCxHU1YxRcmVkGpyc+LgUUn7bo+WSox7fT5VilOyXYyRod8kCr3Y8T7cYs4Q17i6o9+0PH/8GD8M%0AfO/Hn7FZb7l79h6np3eYVacpY3q9hgBVLrUQMyepsKoBYrbSVtfJUjk/S7llH33wMSLCVbvk4vqC%0A6+trxBgePXqEatrrXFWTm2Q8VVWDi/TtGtXIXU0uj43kGstpzyqCo6kcGiNffPpjrp495Y9///9j%0Au1px8eQL2s2K5eUlxsA5DedNYpBbDE311ULV77SC6ULK66hjlfY3loAYJRLzXsA583bkYAwoaWMz%0A56qxNKOKSfk5Immf4MnOhqhirCKx1McF1TDu+9P1nuA9wQpVtMxmCUzrOsUHT9DIMPR7IGlZ4aer%0A/NSaSCvOpASkJh5JXdeoKXhCwhrKhAkhjPhJlDyRjSmxgRurf5n4RfYqyLFvgY3WxMSq0RhHi2G/%0AnTdZuMdqwUyB32nx8GPRn+ImHFoxhcNTFJMZlVlpS9xrx6FMXdqRmxICvXqMs0zD3CHsSIt9nxIT%0Ah1yAazabcefOHZpmju8Cn332GcvlMkUDq7SY1ZUZkymLhSKqLJdL5k0q4yAibLdbnj59iqqy3KzH%0AzPqoO7DbVmmB6rqOatZQ1XXKy5NE4dZSVCtqUrY2gEDXruijsl4t+aN/+fs8e/Il3//TPyIMHfQt%0AMQQsgrOGOGSKw+BRkXTNryDvtILZds9ZBDB2TlUbsDkcmTdqNzYh9RIH0gbvIW3IJQLGIepAF0St%0AUG3QaKgqBa3ylqeJL2O0wphsKseUCBgwBISA4EkbuKu1zE9Sbsp20yVfOESCWDxpsDfGgatxVT3u%0A6xwHj1FL42a0/XYX9cpWkcSkEM7OTlAjCXTE4GPKkq7Im2gVcpaVXUKlMWn3PnYTu7gph8emyuAY%0A1jE176MqIe7YvlN+R3lNFUK5RrEiituhmqrITb8rVna7EejNqBIkd2i30ViKfARTAOq8Y+QkQU8L%0ASD/J2i73O1VuMUY6GaiaBqkMzph0r31q33vvvUd30tJvU17RNqYw8NBFNpsNcTCcnZ2NYPvV1UU6%0Ab7Me25LuLZVjuHf3AVWuHHh9ecVms+GTH32aFhmzWwjixE289+D+rpKfwoeP3md+csZ622Ii+PUW%0AFp5GLPjIFz/6CZvNhusnT/njP/5Dnj95ytXzJ0Tf46LmLXQHrJDKaobA4CNh6PDbRO5r/S+ggvHD%0AmhjmCB7EI2IRSTv7ISBGsVFR4zESsFV6dyYiYiHWeAV0jkaXFUepjF/C1zvuQL4sRGUIA0Pvx72X%0ARWymk6eiQWP0RQ2urhJ4S1p9SgiYKfYRE+Bq7f6m74wT1GNyoloIKcPZlBXf7LCQMhALJfzYa+q6%0AFJm6MccA3RTmPrRQJJdUKKQ48jNIO0IyltbepWTsdogsVmKmsE9eMQJqMOIycGvG4yNGnfTpKMXN%0ASvdox/ZArmDHbkuSolynzN+ifNLETj80/bxEbazKuDmdiHB+fo4fAquwxfuIWMtqtUq/q4zJoHfu%0A3Bn7vSjuOmNm11cpJNxutqjuyIq+JNaGZDFPwXZIiqpYP1VW8kJIlfj6gc31khDhs598wuXlJU9+%0A/GM+/+QT2naTNsyzDvVt2jfdB2K2rAsLPITAkLGrfvhFVDChB1GMhUSHS5XuMYpoRPFEExFtMTbg%0AqhZnAs6ljb2iVphoiAFCqFAiQ9mqIJvYiTtTsIdC396vxmalGpXGNBIyWgr2JudDjSBhh2eU7+wG%0AoCDZCUkreQaliyKQfUWUEtgEYy0mJ8tpGYw2uYCSPkgz05pUfX6MxGjOVzn+SuD4zn1KRL6brl35%0A/yFwPJ0Y0wgOsOcixRiJlR3dsamLc2jBjPwXCqhf2hdHBTNVJoWbU0Dvw+uOrpwhReB8QHOZhJg3%0AqdfMAC/ZzNpH1qtN/ltZXbXjs3diOD09TdePYWxr13VjOcy+74kTtnWMaSkq3x/7DMaIV+nnpmk4%0APz8fx4AzadHqti1XekHfDvQ+8IPv/5Bnlxesnj6hazeJ9V2lnTuVFL7ufUj0BoS0n1POA/Nlq5Rf%0AQAxm5iwzZ1lUc4ytdslx6jECIQxE7xH3BTBQNQNVFYhxAxg0GrbbBYOvGfo7oI5oH7KY32M+O6dv%0ABZEK71vqTN7qfcBaYVafsFqt8BisM9TG4ayjW22IPoWKnRhqDBFlyNt+DGKxEdSlbVcLUcx7jzWG%0AAagql+ruhoDm/ZqNSdR/HyOuStuQxJzC4GOkNmkiWAzGkiMLVVZ6B9EL3Q8/l5W9uBrAGGIn7lwH%0AAyMOUVY35xx934+4EoBG2G7aMbHPmh2Qa+t0Ttu2XF5cAYyEPmNM5nzkvaatSyS5CIJhs96OIX8P%0AiN1nBO8iZml8lAntnMNmfGPqipW+n2JFVVVhYi4sVTFiWs4ly9HYiqZp+KVf/RWePv6Spz/5nLqu%0AuXh2zXbbcflslUK+w8DpfIG1uUB6toZKH6sql8+ej9Gj+XxOlXdzNJqrBlZuVGQ+14epqorT01Os%0Atbz//vs8ePCAqqrSM/CBbd/y5eNnaN5JIARltUztMWFA+4HBe7pcVtSoT1vcknhTsUvPf9WuUB9I%0A268kBfRV5J1WMHO3oKbGRocxFcalvWT8sAXvGTYtg++oz9aoeEQ8Kh6VFWDz5u0e1Yq22zJ4paod%0As7qmdoJtHEJFLwGXSRZSpUzUupohg0fmaWJUGTcIQ4/XtCugCwGrkdAHTEhU/UoM1qTXuBcRu1Xd%0A2DI7dlYQMbkYIibtr5wnyHx2srMuTOI3uKrCTjYsg11ofLQwMkA9mYmjezVNJYCUtn8shDwFTad4%0AzTHrB/Zzi8o1iuKaHgshYOp63EkxNa+QHCe4zhF3rvy/KJyCwRSLr+w1NK11cwhAq+pYr3dkuMou%0AvG+tRUPk8uKCz798zHq9pt12hJDCy9Zauq7DOcdyucTaxK3pu27ksHRd2jCvuELRJ+XR1DXn5+ep%0AEFXf0w67WjumuED5PquqYj6f4zUimhaePqRs7lSNL7JZt2mHgW2bFGvepZIQ0egxREIMCOBjttA0%0AWTJesmKXFPyI+uqJo1N5pxVMHc6Y6z2qcIKjTiuqidRGiNoTzAZnIOgWZwzOKk4gCIhEVAJV3WKd%0A5/LqCcv1FrsVnFEenn8HVyVcpnZzVIeE6cwawKCbLkWIgsdFM27QZfyADANxs0mbtA89OnQU8rpu%0AFe8HmESRQuwJsUelFMAOhKAJdLOSH7QgRqlc2kXAOIOtkqJxJtUwsdbixOBcVmAZWA7tjk9SJlNx%0AT0r0IoTENm23JUEzZ5WH3cpOVgCjFaO70HKxQqaMVWPM6DoWLGK9XieTexjGyVCSDMt+zDPndjsn%0A5uuEEBKgnmn0ZqL0DjGjorymeJNOlFn57am7MeXnnMwbBj+kxUfAOkfJPu/7nnaz5erqivV6zXe/%0A+10uL674g3/5xzx69DtQ3U4AACAASURBVIhukyj9qkpzcsrp6YLtdktz/+EYJfrz732ftm2p8/0u%0AZnOsrfBD5PpqxbfeT+dWs2bsu8F7ZrMZqol4eH5+zqNHj7CLGeoD6/WWJ8+ec3FxySc/+Zw4RLpu%0AwGDHfbPTIpIwmlSuo0I1b2EThmQthhSFM86iGIxaJMpIGXhdeacVjG9BB4d2Dm8NrpoDPuV29J7Q%0AJf9W55qIrcGlerhU+DAQfAo5i7FYF6icBwkgA0gCjmM0WFulaBQpqqMRTpqGsNlwud3SqeKHlMM0%0A9KmWa7tONP4YIz7vH4yk7T3FJO6GqGRLISKSEhf7fv8eR6BXChay43IUDEJtyjApNUWMMWm1H+ve%0A7GMOsAM4pzhO2dQtfZYGlGfHvi3fL0omoawlzJtIiqVEgrUOaxPoba1DpEckuUajizUE+t7nLOIC%0AECdgvIC1Mm66lkpZpHu2iVQo8WZfASEUYuEObB9y2YNyv9PweLn3co0weMIwEFTGPbutA6xh0w1s%0AVmtOTk54//33aZqG6+trVqsV5+f3Rnymrmvunt2hqiyLxYJZPafrunEPq2I5zedznj1dYsyS87O0%0AT1JlUy2YB81Dqqri5OQEhdHFOzs7486dO8znczpRBhIgnLadTdnX6kv2/oQ+IKmEa4yRoGmRFc0R%0AVyyIRVxyT0PeqVJFkGjwmS39uvJOK5j/5//4pzx8+GPcbJF4KeKxVjk/N8wXjm9//JDFvCE2qZNM%0ADCk3o6oJQcYBGkVZzGuq2rC87ohhSRg2OFNR2YYQOjR6pDKIGoKPPP7xj/n000/5vd/754km7z0i%0Aysl8gTH/P3nvGmtNmt13/Z5bVe3Lub5v32Z6psfjcWwUbAeZhJAPMR8IQYoCGL5wCQoIARIXCSEF%0AlPAhSAhFQhBFIIESkAJCQkIoUZQExjgOwRKKGUACm5nEeDweT0/3dPd7P2ffquq58WE9T1Wd8749%0Adg9ji45LOjrn7LP3Pnvvqmc9a/3Xf/3/EAp1HkAZ2RFizri2odusabsOt+5AK8aycGyrMGaF00ac%0AAaOkq1qLJ1DO4oujlLBY27albdvyacyyByqXwUIiKleRcdHYraWBj4GWljbN5mdN105zL32QxeeT%0ASAVUFmkNMN57EcdqmolVWjOTmrkAkw1uDU7H43HKZpaDhtVv2zmHKTYdE2geYmEut3dB5TgDpxXk%0AlQytYk3z+Max7zkejxOfpi8umUtsqpZxh3Fg9J6sNGOOaGuwri3lkiZ6KYtDCHzlK1+ha1f8wT/4%0ABzkee77z7Uc0TcNms+Hm2XM2mw2bzYZf+eVvAJI5fvGLX5RhRa25ubnh829/jvPzcy7OzuWzPJWW%0AtlKT4LoumNEyK7y5uUGdr2X/sQa36jCNA63wKXDz4oYwRuIo57xPc6mqs3RZK8bWWDd1tpRSrDft%0AhIlppXH6ewsVn/hRSqnfD/wx4CeAt4Cfyjn/pcXfFfAngX+J2ffoX805f21xnyvgPwb+kXLTXwb+%0A9Zzzi0/yWp48ecY4JAIKHwNDOGGd4urScnbW4kzg7GyDVre4RtPaiFaRrs0iTq0yWSVCElHrRCaM%0AA6M64ccebbc4o4jFv7dae5AjTx59xOOPPuTRhx8Wmn5JsSlgZ0xCNVeK6MUmxMdAAtqTBJiz60u5%0AGErXIyvonJVJXFUNJYrlpyozNQVficWVb2675kJjhxxKaZQkwCyzliWnpO7gS17M0mURXj1GUL/8%0A6KeFtgwYy87P5E1duB5LzGXJs6n3rXgHSwypBCHdrWZ+TKrjAC8PVNbXEePM36kgcv05xjh/XouO%0AVt31YwHYc4xFGFuXxwjoejweefz4MW+++Savv/YG+92eYfCcn5+L5EPf0/c9n/vcZ4up2jNSEm2b%0Ax48fA2IbHKOco9VqxfXlFV3XsV3L7NVqK55L3nson41IqjZTcJzGG9JsMVNLz91uRxgjOcj5vB0D%0ASQwtiqB6wVgAb4U0OJaZr+NwxFrL+TYWkPmTrMz5+F7C0gb4BeDPA3/hFX//t4B/E/jngF9GnB3/%0AmlLqh/NsrvbfIAZt/3D5/c8B/zXwhz/JC/nC9odoVUceMtEnnu9fcPQ9X/+l93Bbw8XZD5I/84Dz%0A6wZjDWk8oXWiH7OINKlMtieiOnAKN6Tcs9vvyOEpXfN5Xnutw7RXWNcR/FDKGc3QB37l3Xf537/y%0AFX75F79KZx1vbM9prKZ57QGudZzSiM+RbDSWE/0g8g7ZavRjK6ZrjaVdrXj9zTdZr9e4tmXcj9jt%0AWnYtm0k6Q05YwFhhbEIiJVVKOUvXrTHG4axkGcMwQAqkOJYybZi8jqVjlYpdRkNKGWM0qdbem3NS%0A3xP6gA9gUqRtGqxtpOOiDFjDKYqlRkJPGUjbtmyNQwONkjEEiORcy6GR3eE0OxG4BgqjOgC2aVBt%0ASzYZryJYyTzH00BCrDas1VM5qhuHNob98Tjt9ADn5+ekmBiCDIkOdeDQn0hByi2r5Utr6Uod9qcp%0A6NwmybqcbRlu92SFiFoZjVOWIQSePn+GbRxWGx599KHQ9VVmVc7d5YOHPL95yl/56f9BNJO3FwBo%0Ac+Q6SWawu71FKcVwPJGyZgiZcXfi2U66ZW8kRdtYLjYrtusNZqMwVgDw00EybH86MQbP6dTzjW+9%0Ay6/92rd4/uJI8JndmElRyKA5ZXSzWO6qgPdGBLuazYYxZrbX11xeXnLafcjt7Z5fvb0tG8EsgfFJ%0Ajk8cYHLOXwa+DK8cflPAvwH8+znnv1hu+6OIsf0/DfxZpdTfhQSW35tz/kq5z78I/HwJQv/Pb/S1%0AbDZnorcxQggJ3Rrcac/T4bGAoNrhbMPFxRusOothEOJW8BzVEecU2ANHrzn4J8QE/fHE6ei5fXHD%0A2frIehUxquzqKeOT1OeDHziNPafhiMotWW3BaE7DiT6MDHhiDmANBuE9COJvwQR01ty+2NMOA+eX%0Al7IrtS3VudAYg85q2v2VylhncNpMO35kniYX4HOWG8hZFUbwfZW9u/IFwNSKBDBGF7kCR/KBOI5T%0AG33Zoq4/H8viruDj4lq4c30sn6NmOF3Xye2llKn/d5m5THhPeQ6dKd2ODKnq4PgpQwHJPsYCZtX3%0A3Q/9NHJgbcWJDFqbifpfP+uKy0zcnEUWt7zvfd6TMITl59vbW959913GcWS73aJUeS/Jo8XSmr4/%0AlkFGUCqLWJhSKNtO/6+WKW3bYp1G6XmOLaSIbRwffPQht7c7+uE4lX9jSISQkDy4MJ6L0qExRsz+%0AtAWt2J5vuLp8gE+RH/2xH+eLX/wi+9snfOMb3+BrX/sawzBw7OcZqk9yfL8xmB8A3gR+pt6Qcx6U%0AUj8H/D7gzwJ/P3BTg0u5z/+qlLop93kpwCilWqBd3HQG0K3XbLotKmmiTwSboTV8fv0DJBMxqkFn%0AS06voVOL8QFyJvUjTRxotUY1zxiSZxiClDDjwHga2d++YLd9zrrboW2LSplISac9uNbSrR3bqzM6%0Aa1CdJqjMMZ3EU6h0IJTR6BClfQySuVgpa85Xl2WhJ5KSBbZaX5b3nLFGLiYRsRMFemfMxJzNtkFR%0AGMTKTqWNAJZOamwgdaOQ6HojLFU02jrQGuNabCulQoyZFMfpOXITJ2yk0vlDCOKXVKQqaqCqGiWT%0AQVu6O2fUjwHvI03ToYvNynq9Fa3hKrthLdo4xEtJEUKagGClFPv9UfCpMlvVVlfCkGlMw9n6DIDD%0AreirrNdrrLJklUkqTJ0ya4sTw2rF4XCasJ9yrU1lXwyDOGVaAyhOfU8MxzsB0BbNHuECgdGJ47Hn%0Aq1/9W7jG8JM/+fvp+56v/9I3CSHQNA3DMPD+++/Tuobb21tcoQKEEGic4+LsXDJYJVPv1mmSEvZ2%0AImJti7aapBLR93RdQ+9bhnFkf9wzhEBMkE2ZrxO9Etab82nzurq6olut2Ww2NN2K119/nYuLC/7R%0An/on+JEf+RG+9vVf4fWvfY3zt99h6D0ffPABv/rff/kTB4Tvd4B5s3z/6N7tHwHvLO7z6BWPfbR4%0A/P3jjyO4zp3DuBKJsaAzq7Qma2jpCCpgraPr1sSTaJLGQaES5JMmJgN9ghDJKWOUJRXSk9OGFAJh%0AkN3b5kJKy2qq+ynAremkU+JJECM6OZJKBCUkOEJiZRy2toMLdqK0ZnN+hnPibbNarVhvVlirJ+Ka%0AdJ5SIarNZDKtpduinJpsV2qHyRhLNZcz2mGMdHaqKr7WejHeMLdxJbPxd1rZ9T71+7L1u5zhgRlP%0AqUS4Je9lOevTti3GlQxJzV2yJdJzn71bMwSfQRnhDgnnqCgYIixWZ+R/j71kjBo1jWBMoxT32MYV%0AO6puCACa+jkVKU2jOR57+qGHPMtr1scPw4G+H2nbjs36jL7vefDgAV3XybR00chZr9eEceQ73/kO%0AgBAyK3t3wQsSw7X8UmYUQibrSKO6iYltrGKMUqKGOKKdLbYnYI1DGYtWEjzXZ2vpwDnH2dUFq9WK%0Ai6trtNZcv/4ab775JtcPr2hXHWdX1zx88y2+UJw9m/XmY5bmdz9+s7pI93nF6t5tr+Id37/P8vhT%0AwJ9e/H4GvBcU9EqkErLLoBzGtVxfvMYQPUo3xKzpRosNBnNMmGAwo8OojjQcOY0jSgeaEElxIHsN%0AyXA6nDgdjzPBriyCMSR8BNU05KYhGUvUitEqFBZVja3KnImPI2HMXG82NG3Ltm1lAtYZrh5cc3V1%0AxeZ8CwjjdLVyk7lWnS/JcRbvJmuslQtGMAn5P3IBbxYiT9L6VkqhVSo8FjVlIuv1ltVqxdnZBW3b%0AitaMMcQh3VnYMt8yDxR67/HRT+VOzXBqN6lpBKupXSUoQdFYoQOUFB1TtWJlVklrIx0yYwgli1oG%0AmZwzgw8oJ52PpeRF/R/1NZ5OpzszR845EpHVakXXdTRNN5VRc2k4D0CqLCpyOVWN3kHkF4xmUxaa%0AMrrIMpzwR8/Z2RlnZ2ccDkK2e+21B4SQJENxDus0773/LrfPX3B9fSmf5VCmsr3Y456vt6zajsYa%0AuuKNtV512Fbmg3zwgJKJeqvAZh4/fcb/9Yu/wLOnL7g5DJz6nmQALK5b0bgOV4zcxhx48OABFxcX%0AvPX2Z1l1a15/8w2ca/nxH/9xPvv223z2c+9gm4YvffEdfugHv4DRlidPnvAzP/PXPmZpfvfj+x1g%0APizf3wQ+WNz+OnNW8yHwxise+xovZz6AlFnA5P1QL4qkE9koxlh2Xp3RjcGngNEW17aQNa0ymJjJ%0AhwEVLS5oUEHIbX7ErRU6QBojIRhy0hyPIzcvduyPJ6wR/ISYSdFyOpw49APGNiRjsO2KkCKqqMgp%0AjTgUKIUyLcZoAUe1xbaNjNcXJqZeEO5ql2G5m9VFVlNb8qx3S5YZIqNFt8QYg7MtWvvpObTWpDxi%0AUqZddShTMiQFtnGEGDGFAq9NnrCF6TNOiSEEnLMvdZZqmVSDS5UjgGUnJ06/T/ydnDBZYRuHiiWz%0AKFPugudAHYKUkQ6F9zKAd/Q9rWuARNtqYkylNGsIIRFCJGc1Ad/LzKWS1kJI02uer6e7MpoyuiEU%0A/NpWT6X933Udgx+L2HfEOsP5+RZrRRzq5sUOrS1Pn37E2dnZpKV7fX3NpltxOBwwxvDicMJajXOS%0AFVX+TNvJOELbNUXuIZBSkTfVisH3RAWb5hxlLA8fvM4YMt959E0GHzC2ISKjAk1r2JxfEFNiu7Kc%0AX1ywXm+5fvCQrut4++3Pc3Z+zg9+6Xdw+eAa2zaElGgLTnV7+4IwDFydn3/3lf8xx/c7wHwTCSB/%0AAPg/AZRSDfCTwL9d7vPzwIVS6vfknP+3cp+/D7gA/uYn+Wf7PJCVQTm58CtYGGImEmk2K1YXZ5gE%0AsT9wePKYxitSMuSc6P2OZ/oj8npPuDAYtSWOMPaa02nk9vYDfuXdn8GHIDKWSrFuL0gp8/ij93lx%0A8KzOHhaqfcJaXSxnk0x0lyNFTzbSMVmfX7Ber2lbx3q7nczPQSam2262AJFhN0cyVaskTxT6nBEd%0AmpjISSaYKw5jTYPSooUTwtLOVaG1GLR37ZpVtyoMWsFgqt9OzhnvenxZaMF7rq4upxIpFtJazapq%0Aa9R7z+l0mgJbPXLOWNeirMHWYU5bXrNWGJtRKZEkZk6ascvWawhBWMUwlUjNeiUt5eA53g5TBvPg%0AwQMuLwXfqjat1Zd7OidT675ydObzNVmkZOnIDeNQdF9a1uv1lMmBtJdnLtCOw+GEsTLKcH19PfF+%0ANpuVZHpGc3MjNrIomVJ+46GUK6vVCmcsZxfnOGexVkpkpTLGyoCqdhbbSeft5nDL4TDy4vbA4Thy%0AdvmAB+2Gk5e2OrajW2958PBNcs60neH66iFN0/DwwZustxve+sznOb+85OHrb0n2mSI5WW6ePOLD%0ADz/k0UdPZDP8LeTBbIEvLW76AaXU7wKe5ZzfVUr9GeBPKKW+Dnwd+BPAEWlNk3P+20qpnwb+c6XU%0Av1ye488Bf/WTdJAAkokkI0NhShl0LtTvMZKTsGSzgiEFwhg4nQ6EoNC5IfqBw7jnJh2JY4/uLLgN%0AY+jxQRNzJibPi/0TDqcjIUsXpLNbcgbf7+n7AW06tNFCjNOGFD1aZWwJSNooXPa0q45uvWa13tKt%0AZKdabzeya7WNiENngzGJGKWVOrFssym7eURa1OX9pwLYVo6Menn4L8YoFiVKNFGUMUI2bBuUNWRt%0A5rkj5mBUAdv7shJLDk3d8ZdlzMfhN1krTMFoqphTzllwhKp5kupIg5RNwSeCl4G9Sd4hgzB0SyuG%0AQh7LoK3DNi1nF5est5I5xCzvq7onzhjWPPgpn+Pc8ZrYtuUxwmKeNXOAiddTy9DR9/hCaOu6jtub%0APd6PZfBxmLKiZdakNazX4nNUZTGVUmw2a9qmoWk01sg1lDPTOIgy8jpOp57TIOC80Y7Lyy2r9RbV%0ArElYhiiBfbM9I5JxSrFabYoMZ0fbrOnaFdbK+Iu1DTrLBvLB0xtubw74MZFTpO9/60YF/l7gbyx+%0Ar9jIf4VwX/4DYAX8p8xEu39owYEB+GcQol3tNv1l4F/7pC/ktc+/yfZ8S9uKE1/f9wy953gUTsOQ%0ARp7ePmN0a/LQ04ceNyZSEuDq5AO3yTHqDn104BKKIyllfGzwyXAcR/qQGcJI3/c8Cyfhi4xzCzWn%0AQAienBLn2w6rZZ7FGUOrxSS97VZsz8558PB1ulUjE9ldJ1mPEtFxrTUKXwBTMIV2L06oipwUWUWq%0AkXt1CVgS2Farjcwv5czoizxlWaiz2n/VJbETzlKdz5dM3UrCw5gpMxmGoZQZM7mulh91EdXFu2xT%0At60El6ZrJ2B59H7qrKmUCEO6E8D2e5lMHgueI2DtrFObjS5ByrJuWx48eDCxaJVS7E5HAhnlLGZh%0AZau1XYDQ84KfWL0+l7Z/EWvXMrYwRlGzqwzqSmhL6ShaMErRtmseP36E1oa27SZMarWy3NzclGxm%0Aw2q1IsU4lUV1JGDdrTg/2wiD1iRyLJ+nSmCMfNcis+DjCHnDenOJbc5o1mcY13AKmoxm3PcMEdKh%0AJ2RoY8Ao4Q4Fr2jbW/Y7eT+Hvefy8pL33nuPR48e8au/9C4vXrzg6dOnhTR4153yN3p8LzyY/5ll%0AuH/57xn4d8vXx93nGfBHPun/vn/o1mBbWzo5Gu3WaDfOtpfAEAaMXonqGKK6r8aIHwI+RQZl6INh%0AOIxkK+6IksFoUhRD8qxKa9kasfCt2Iex9P2Ow+GI9wPOaq6urnBG42xTwD2HbaDp1lMa3HaOaimy%0APARXSRPgqKum7D3Gag0G9TF1IcdYxatl0PF+x6TyYOr/njCVBFrf1ZepLen7WUrFJO5zWpYL9D4/%0AaokHLb/X12D07AaxxJ2W+EcNStbYqSxRpZyrQeXy8vKOFMMy6C1f4/IzWQbDZVfNWovCzEG2ZHem%0AlAp1Iro+z3LIU9rhUvbW54sqlnJQk3IkxIAzFues3G40m82a9Wo1nf9hGIh+ZK1boTuUqlM0iDLG%0AOcI+EYME5OAjUUVSgqg0ISQGHxliAcEHT6ys3tsjAOab38Zay3sffMhmveWjjz7i+fPnfOPrH9L3%0APbvdoVjW/jbUgzn6ATN2BKWBSChj77f74wQ6xhhZuQ/xp57D0xekwZO9XHBj8OzGnqQgPhE9lZDE%0AEsK4AaVGss5kHH0/cDrlyQTcNoGQEtElTnnEp0S3PeONt9+mdRZDpGssFtiuXuPqYsP11SUX5+c0%0AWqFVJOcgDEvEstZiQa1xFlBVJ8bTD2VIzyiSEsU1pRR6FOU4qy1GWaIPHMNpSttTjsQQwSt0NPjF%0AvE/FHqR1PrdLJYsAg8FqB0kRhoBJcoH7fmT/Yo/GEDUYbXDKoXImjCOrYrl6CiNN19IPA6ZxtC6T%0AnSIQBWfJTIOEfrIvdWhlGMKJEDwxJ0Ly0FoSsL26Zru55PzB6zjXkrXMX23WawFLVx1OK07HPSnU%0Atr0RrCoXoS+AmBhHCZBGaRTQOlnUp9MJnbLwbbTF54yu5YPWHI4nbm9uudlLQn5+cUaOYGyVrEi8%0A/dk3ePr0OX1/S9cpUlR89Re/StuupuDtbMPV1RUxBJS1habQsF63PLja0vc9PkRWG3GVxGj6YSCG%0AiAsJoxV69PTjLSEcOewiH33jwDAYdntLHzK700BMqYw6JA79bjLKEyKnYEjkTAg/L8G9jFfY9LAE%0AxwalWoQF9smPT3WA8UFAxb7vC/Aok6T7EmCqclijwQ8jYXeEECdPGB8jQ/QkIymoEOPstCsBUwYx%0A76wLHZOCDdQOj9GO1WpD6wwqjTTO4JRouVQ5guquiEKMsNSsPCcLXt7bcrddqrLV1yBtaC3lnBer%0AU4WZanm9kGuoO/h9eYI773GBR9wnydVswpg5w6ivL8WE1ndlEmAWpkopodJdqUr5Xy9bpizf8zIL%0AqmzW+iUZTEezEkMxZ21hw86Pqe+7vt5qz1r+OH+uCz2e5XfBSkopuQCcd7vdRDCcmMdlTkkeEyfW%0Acs2IatdPa7DWsVq1U4fLdR05J2H3ao0weoUHVRsAYr6nCXEeTM1K8JjzzZanjw8cj0eePz8yDIaU%0AL/BRE4M4L6SqB91spvNQRbiMaQQ8Vxql5/OimbNZyfI+0dKcjk91gHnv2++hlGG32wmduWiaVqP1%0A+tW2DoOiU0YMSSrdXil020jrFnHHUyGgjBbVTA0qKWIOhDGWnVbEmP2hti5BK4ttpc3Y9z0ki02R%0A7AN23dJ2ltdef8i6c1QqeSqOgfJ8C+0nXRfvLOKktZ06KdbOE8h+GAXwzSKJMI4jq26DsRXQjHg/%0ATubxNcAsy58aaOrzj+M4YQvDMEjbOSWOw4jWMh3tvSdkWYCSBciHlSJUHePTaWD0MijYWYcqnaOc%0A81ThTQqERe9G5jgWZYxWaCeezNuzM7bbLasyndw0Ha5zU4AxRtTwVYoYDfub24nWH7zHlG5XDTi2%0AlGldK+MN1lpI8rk2xtGPg7SgrSVmMY6rC3+9XnN+JeMdmUQMafKntlZEpOoYxO3tLYfDgc++/aZg%0ALdoyjgGtrEzmx8hxf0tKI6hAiBDjDIbHGDkcdihr8MXZIA8yvjAMJ04nw/PnO14835N9gzUrhtFh%0AsXSteDEFBGsKSco2kxU2W4w26FjKU+F6kwv7W6u7ou3fa4T5VAeYZ8+ekbNiv98XXKAqfsmHU/VN%0AlBFvGKVtoZlriIgeS0kgfRRMxiqNJk/ptJQaS03XLI8rPkAiylMnqetsSo3+krk0jaHrRCVPqUDl%0AXIjO7hKzKGb0dVK4KN7lKKpnKUQSxZYjlgwIMQgLsUzNpjJV7USEqnoZpZIqV07N0p9nSaqrwWs5%0Ab1SlMkWrtQSi6En65Zkjae/O2ZAys4r/XSzGLDCM+ti72VTdrV3J/pbT40rNjNq2FeKiIpODZ3fb%0Acyq6KBMOpeb3mbOUpFrLRjLBC7riTzUDMXfxkMKBqcCs3HdWyIOZHQ3CN6oaNA+uLgQbiqD1iFJG%0AyjidMUbJpqAUeoF1TLIYWmP03Wy2/rzqzlh1G1YtnBqFD5aURAGAbIgKUlIkFCZ3JXtWkCygSVmU%0AFVOSjWbpXS3ZXQ0wvw1Fvz949CFGz0JItXypPIr1ZiMlQyv8i0YZETaOkZw0VfQo5kRfav4xyG6W%0AtcJgprIgJcRrRhVae9ais4qUKjrPbn3ZGpJJqJCw2rBdNzROfIw6K941AriJZpPVxZyrKLbVYbq6%0A0AQvyJxOAyEcpuyjsXIR7nc9w+A5HkSq8fLyku12zcWlkKO8LwEjp2ncP3jpHOVOFna9zziOk9RA%0A38tCbYrubkpzhuOjx5M4W29wxk5AbCWoVQ2TpmvZbDYT2PmqkqjqtoRQFOdiJCTRznVtw1nJXi6u%0Arlmvz1lvNyjmxS90/cCzp08Yjgdub55zuN3Rnw4Yo2WAsFAW0Eq8orT4RtWWdFdeT8yiWdN0UsZ0%0AXYcpbWrvPShh8I5RztPt7pYUM20rejGHw6l8jkLfX62ETWv0OJVSXSuZxP5mTxh7rMsoIi9uHqGU%0AYu9ErsE2JUNrG3S0UwDUtZzXmdPhhO8DOWmsWZGS5XxzzRjh0EdiVqADOmdSbCcXSYOGBMGLBnDO%0A4vqYa+mLSI3oqeHwW8SD+f/TITR2M128E7gZ51paKYWPacJKcs4QBFPwKcoAG1mwmJRwxfKCXH2D%0AFt4Y6IJ9yG6TKO3jxY5d+SNWiVGZsUqmBhZeRzISXPVeTRG+MtNttYaX/z8vyhgyQ+8Lqq84pRM5%0AKQ6HE0Mf2O+Pd7KPppUMLuZC9S8BZsmqXWIPS12Wir3EGImq+kbHOwEixYxWMpFc6f657HpaGYyx%0AWOtkJsYasq7K/1lcAwr+VHk4UWzx5iyGuQuji92LLSAlec6MJHAxlXjL9wLFlZIZiwLpsuRcNXeY%0AAk/FJ9q2ndjRy5Z+Xwzqh+DvqNOtVqtSEu2nUlRrLS1zDDmNpWNmUU6m3U/7g2S2zmCtJiZ5brlm%0AFG05f9oasgZtEmeYzAAAIABJREFU5LwZZ4olrMyxbTYbxr7HD620pz2QFNEnUlaSuSIbq1ZCApyw%0AqZI11sRJKZHQ9Fk6i3XdVKXCT3p8qgNMVqJnESt3orIzo5z028MefTqSCy9EUkFBymuJMLuUyIVo%0AWwfacP1QZjZi9FhjGAZhhO52O+lOHY/krBhD4MWLF4y+J6cViohWBtfAql1zfbXh+srR2ESOkdOx%0AR1N9d2TnoXSRjDE01hCtxuDKRG9ElU7OeBpIIRJHCQKHw3OCTxwOwv85HCTwPHtyw2rV8jt+x5c4%0AO99g2k4CRwnIjetwbbGMDYmQJJPzXjCDmsmEIOP9FY+pkgM1g+nHEc4v8N7z4PKKnMUqNzJjO03T%0AiBqd3kxmYd77SWW/lkGVCZySYGFVg7ZpLc1K+CRN1xYKfVdK1GJ7EgKh8JSqTEPbtsQwklLEaE0I%0A4+QzZJUmpAhJ9HCbppnEn4yzXK+vcW1DJdedhoGnTx/LgixYV8jz6wc1GdUvRb8rQzvnLFlLLsB6%0AFJrD1dVVWewBo8G5u2LlNWMp/2LaMGzblOCraOw5X/rBL3L70PPutwcePdoz9uIMKhKqep6011JS%0A5xwgI6xwVcZlKwYo4oeY7ER2M2Ume6vv4fhUBxi4u/P6Ol2rbGE6Cuib9Rx9dUkBQ5rBVIXwEAAB%0AI41hszmbeBWKVIDPHqdFrWxAdgY7DPSrhpgGIJByIGVwpmHVWbbbDcb6kqILpi8lQZBSLWdQAb0o%0AiaB2RDQplbkidJmIhhhFNX7oy2IvAPTxIE6Ph8MB62T3fDg85OKhSECYctHXC3/5GXrvp6BSxan8%0AME64TMWfKjBbuyzCJK6maNXpLKEaiyoTycU9bfG+7naP6vNPj1/cVxUm7fQcd7AIveDL9Av6/8KR%0AgbnjVUWzc55HLpqmEWxk8bnPPJ2587Rer+Vay4WZXAhwRomEav2/VVOmjl8opbCmwRmK/1YkxWJs%0AX3GgGAoWM58L2fCkq+gaU/SPq0KfBAvrpKzZbFr6PjF64WPl3JWMJE1xQSlQOk1Zm4Dt4qAACxxq%0AOr43gan7x6c6wIQYyWpO52uAMaXlZ6wpv4tdRQVtjTF0RWNW2LMzHpC0wlmHaxq6TmaGrDYcjjtx%0A6lutaawjNnL/2/2OmAaMCjROY2zC6oixic22YbXRtK0V98nsofBfYhwl0BQUPyqDjrFweuQC6I99%0AaT/e4r3nsB9Kq1T0TsJ4YhwDh/1A3w+8eHHLYX8iZQkSH7z3EV/4wjv8+O/5cay1dOsVfT9ibS/a%0ArYhQV4iRJ0+eyEQ1eZpI9sNI8H5hgpbulCBN08pEcmYCM0GWwdlmhXEFmHVOsqQiCmWsBZWnx8SY%0ACUncC5cdJIoMaSqvSZmZoFeB4pwzh8OB43FfDOcD/emESjNIrID1Vqago5fy07WOxkinpnpca2sL%0AoB0Yjx6hz9vS+hf27+gla0qqBDJVrFdLmQSC0ez3x5npHCGPRxTQmAbTNGVhF1+qINm0yoGYPNkV%0A6YvSpEBLGVkHQinuo0plEieOhz3Pnr3g9uYW0QEykMSJMylQJXMyupNOETL7JRvXxwUYKSxLX48a%0A3D7p8akOMDAHhlqrL2+rXaQqiwhMQWbiWyyeS9q2jqR0EVaStrDK4h8dQpBOTqp8Aek45JwwRmxF%0AGivAsDEiRqRzwmrIOUIxt1ITLsCEzVAYmLa0JkMI7Pd7drsdz5+/YBwksMSYRfvDJ1KUVurhcGQY%0APCnCOIo4eIyZm37Ho0ePefHiBev1mqZrp0ylKRlbCIGY0sRMtWoB5Hov5m6LADOpvKWEKY9XBf+o%0AM0Uz70PPi/we5lMPwQK400KvTpr1MaGWS4VSHxG94TgOU8lWXzNRgphW4GzJYJDsMYQwLVKtdcGE%0AStah706QN22Dc+3EJh6GUr6VwFXZ1d57qkaMYDerwh6eSyg/RoKXzFrK4IY6Ja6VIimNrjNmQfCi%0AigUJ4Cq4Vc08tZ0B38l5FE/TalJSWAMRhbEJ0XuXziVZoyteCKjSUVoGl9KlJn6PJdH941MdYIw1%0A80Ae4GyN8PpOqqkrEOysnKoFUcxMA4USeEKcnQ2X5DSjHc7J7uW9R6dA1ooYRiBN80VNq2kbS7dq%0A2KxbmRRWlawXaHVB7BUQIxlFUNK2zKRCGkzTxPLpJB48+92Rb37zWxyPPfvdce5GZM1udyRF2GzO%0A2Wy2PH/+XPgboee9b3/Iky9/mbfeeou/+8d+dGqzdps1Sok9RsqZ999/H+895xuZnTntduSYUN6j%0AymcJacI4Qgj43GOVpnXNBAxX3kiMEZ1mELZtW8hqUWJJ50V+Fybx6XTicDjgnJD3mqaZxj4qJyil%0AxO7mRpTuTqIuN/T9hBPpnHDFF6px4lVOzsQcppZ25bzEGKXrtwDpvfe0RhdAWHE8HkFruk5A3FMR%0As/JFVVBppsflwpepEhbSASxujM11uWpVySjUxINRqqr0lfKtdEbrZ22ciF5N5D07i4c5Yzm/2KBt%0Ax2ptefTRkffe7zFeE3PAZPBVeD22kwWuKoC9Woyd6GXsL3SK+pp/W2YwFoXNs12FoCm1H6kwqnQP%0ADGQ1X2SqzH5MABq5PgTKzEjItZtSuCgEcvJkepz1+DFPbWutNT5HDKKx0qwa1usOZcA0DqcyKkes%0AaYjDkRQ9KlXzM4VbCfv2eBpQLhHCWDoyAzp5GqW53G5k0NB7DoOUSofcFlvSki2UToFXis3ZOdq1%0Awjw9ep483vH8yY6rayM0/7ijbR3D8URIoBGx7nAjbXAVMlppYlb4ECVjKOJXOWdMUjTW0qDFSD1m%0AbFMkPp0Th4YY6XNExUAzSIctJ0vyvmAgiuyBIGm4ihkVBUjVaHKy6Lyma7ak0BBHGWDse8Fb4iBB%0AYhgHVNQ41ZCQNjk6T3Nj4rV0QqskA5Nk0LLIJWwqkpZz4OwabcpAZxoxXekeeTGME2hF4bIBDNFr%0Akl5o6MQgZeZ4khKJiiU1UyCLOZVZiYRrHSFATIqcNbppSMmXIFDa9zlDoU+QQSeHDkVvRyUuL1as%0A15pxPPH8+Qkfbwle40cLdFh9TlYKrwYZfcnlg4GpMVLZulNmn53gNhU6+O3I5L1LZZ7brYqZsPVx%0Ax8dR1JdkrOk58svPp5S6AyZWzkzbtmw2ax48uOTiXDRP1XCYnqM+lkIU09pgitD0OI4M+wO73QGj%0ALDkqrG14/fU3OJw8KWrGMXI49YxD4ubJY2IEY0Qhv19JG7ZrWl7sTrTO4VZbjodn3N7u+bV3v83u%0AsOfi4pz1RohiWQsLV8SaAjEc77yvsZROw+kgi9qL+JGk2cOc4RX6ui42puZ4RBuDidLOPex2rFdb%0Azs5EN9f7SIxVUDxOO3bwImZuraWp4wohMA4D39wfirh3Eb8q4zF1TMBZhVINOUqXKk65f0brXPAf%0AVbSOpWyu5vSVuZoSZQRkQcor5+pVR9DzqEgVDFsOZ9ZrqtIO6vmvGcg0WLm4hhN36QDL4VBgGgfJ%0AOTPmTIqG0wlW68jF5RZtXgjJMhcTwdyAmqU5AXL52ahfvxb6buvo1zs+1QFmecjFke+cKKgfzssf%0A4t1uzct/W56Mj3tsfbxMt5rpQq8lQWV71sfcYalyV+UNisZIbjF6ZOw9YUyYLHYkSiXGEPBRkYtg%0AljKaFBNt47i+vOL99x9xvmlpW83ucCRtNlgtIGsG9rsjbetwztK0VnSFi8bKEiiXVP+ufENOZerY%0AiEq9IeODCKWj1ZS+GyUX7zAMKK1RKWBDoDENOamJkFZxk5QWn3W+y8+pxMVQuCf9cIKUca6dPlOl%0AFKkEElMcLKtIesq5WMzOvtKSwQp7lrIpUF0VsiJGLxyoLJ9LTkm0hRYb2B3+UHr5NS9nrmrpqCZe%0A1axLA7PP+JKhWwPM/Wu0soWX116KAkYLRylijOKzn32LwyHj45FhyKWsyxi7ml9nBYynS/kuc7ey%0AzGtWIxjiJz8+1QHm4zIYlj9/zFEBuPsBRm6fW471eV4KEPcCgzEGw/yc9WIehoE2JVKMpBjIMUJO%0AqJQnglgFRTebDaZvsFdrma86Rlrb8vTZkdvbntudJ0RQek3WA32MJKVo11f84I/8GO9+8Dd4uhv4%0AyT/wh/j2t7/NN3/lGzjnWDcdKUduDicZ48fQbte0NDKWkAPjWFXjZp0Xpw1JJkAZgi9gqGBQzjmi%0AKqbpMU7Gda01pNJtEjfCgPGe1FRd4aUsQzmPYgE27cxBjxil8T4Shj27m1v2Nzv8ONKYlrbY2Jq1%0AAKtdYby2naOxhoxClwFCRWWmzgFdAqaffldKRKgyiRAHfD/cGTOYx0TURKSs9ioxsAiWaZJ3WDYa%0ArLVlunu+rQpZLbOZKTAV4L++hvo6lh20msE4ZxlHj9KRi8s1WTne+/B9YZjrgHWWs2YNaE7HhcB4%0AEa2aTsLc0C7f717n32sW86kOMMtDPoj0UsD4uAym/q1+iPdv/24ZzP3/Kx2JjCq75DKlrRdI/cpJ%0ArPV0huoOkHMFlYVBbLRjsz5j25X6/PGBECB4CiaS8WPxF9aGR4+f8PVf+QbHU0RreOMzn+Hps+c8%0AvbmRwUAjbdZUiIH9aSTFTLRpmjFZBs877/3ezk02CwDcooyoCeYkDOoQhCjHEDAOYgBjMlp5lDIT%0A+7V8euV/xEL3F2wp20wg4ccjyQf8cWC/2xHHJGWfKRPjR1XsTzq0gRQ7YtOwahvQwnmiUOpVKWVy%0AKp0jFaZFWkuu5SDo0gkB5uC0DB4Vw1tqKtfvy2xG5uHmDbFmLctMZrnhVenQrBViEcD0GgCUFVcK%0AciYH6Z6lnGnahm5l+eIX3+HmJnA8PWG/DxyOlYU9O1kuM+mPWxs1uLwqy/+NHp/qALM8iTOrkjvf%0AlVLEe6lmXUTLD26ZjlYDs/s72LImT3kWkgZQVrFqREqg+kWP44g1c6CZT9r8ewieUE5zPwwYVmht%0AaJ1l1V2wuz2SsRxPI93qnCEmHr33hJwzh6gIIWOt4m/98jflgtWa/+Q/+y8KAS1y8HuGg3Stmhau%0ALi8Y/A1vfuYNQsqsOuEI2cYxBo8P0n7PKZOKL7XRBqUt5CJPGhwxK4LKNLp8t8Ko9scjicy+PxWK%0AuyKmxOXlNU0zsl5vpsWsMCWw+Am/CCFw9CeZjt8f8L3HosgxMewF31i7lWQuD5rixNDhjGW1bnFa%0Asd2usc6gkYC/Wq3QraPrZveAeq5zHheSnWXi2s8MXeGbgCjfKWKsNq1VVvPe1HF53kmqovytWZip%0ALYW6prJtsZhrIJkCyr3nn/CXcURrTdNYXGNFJnR4yi9//avc3ia+80FPSh0xrolRJEjvl+X1uSrW%0AOF+nubz3er3OGNInOT7VAeb+MZ2EafN9OQP5uNum29Urbls+N3fb3NN90xyQ6t9EJU5o/rGURno6%0AmYXPEiK+nNhhDDRG4Vw7qdkBjIOXUYDTgI8JH4pujMw4QC4BwVRalAxOZqVJKAYvBl5JZY6nnqyS%0AuCI0DpRmqVa2LAsTYHS+U17U7yEEctuIuDSSGaCUmMbnTFAZFeu8Eex2uzI2EOasoDCuK2ekqu8f%0AxyIVcfT4YcAkTY6J03EQz+9GFOR2cYe1Mo/TtJacz0o2cVwYl8k4RBPXkA22UBm0mc+fBI9ZByeF%0Alzer++9/wkzyrAD4cdfK/etumUHU0uvO9VTJb3rmd9UAmFIqHU8lk+oY2tYSk6b3EtQ2mw0heJom%0A4b1wYyr2hEpC652ZWPIrFVqoX98fIszfUQFmqmHTXelFFmh+Pe6f+ClbKR/2MmO5/zjZfedD1VRc%0AzYSrapaVUsIuyqUwjjIj4wPei8REH6pFqeKE5/WHb2C0KSzeF7y4veFmf+DYnxiTIuZiqhUzKssg%0AZy4SEgCpTCdnmXqSCXGnCd6Tdj03xyOfffoC2ziuLjbEqKlSnXUIMKfKBwKFfIYqJkKRqEhZLtSo%0AQItkubAlyiLtoxfm7TTxnOl7YRxrZcvOqaZFFkKaNGtvbvtpZCGOMktktBMj95wZY0LrQOw9TkdO%0AvWQC+90ohu3nWxprcI0p808WO57w44x/WFdJgKqIk52mzKK185CjSFrqKbBYY1/eXPLcaaplTxUF%0Ar4GnsoXvb1o1y1n+j9qsqMGlNgtmIuLMUhZYwHLqRw59QGtwjcXa0oaOiZxNETCfwecaA3WZ05OZ%0Ao0IgLfSOmsHJivhtjsF8kuNVgWb6vXxNu8W9C2Lefea/ye5wV2u23i/EQMO88Ia+ZxxOJB/o+9MU%0AYLTWuKYjBbmfKXyFYRgmkScxLK8qZYvXneasSNimdSZIMpuIQ2NQSYYIVYDd4cRVP6KMk6wqle5H%0AWSBJybwNUFwNSseoXODWWvwiyiZkMrdiCCkl1KJ+r4VJioCupC1dypI4aacMw8B+7+cNIAmPxZcW%0AdmXlqiQunUlnQh4nSr6xggU1rWW1amlswpqOloizQpWVRSeBQneOGKskhmwqYRinQFTLmFr23i+t%0A6/lfljrAnQCTc8YPd9vUy2vvfgazvDaXAPMS/5nvUwOPPFfTNEKk7AzOnZBJD+mUaZOm60QC05y9%0AKFW4OZM05vcnNPwdFWDmrGS+TanZlnSZtdw/ydN3LfjKnVbk/SC0WMz1S6VZVvE+j6aS1Kpv0NAf%0AiaPH+xHvA8fRy+5nG/wwcjzuSS0oGmKWxedjmQHKItwtC1pNcgPC28oklYmxXjxF/S6W1JiIQ/iB%0At7e39H3xxlai+2GMsEQFGwpk5UpEAEIJugspSCnDirhRFcLKkq2EUAzXarkYZ2fKucwQ/k9fmLg1%0AwIwDZWE7WRxakbAkFVAYfJlAJ4jDgg51pkwykxT3tJ0j+ETbJowVnCXGjA4KZRVkEeQKXkSzkwy4%0Al9c4B5GagVQey9KUbvl75bJMAbXwYiZ7l3S3lV2vo1cFDbRcs1khKotpFh6vxFulRK608nYqHmit%0A5eLiAnJgu/WkmIjBkDFolXhVq/u7raX/r8ffUQFmwkAKr2Eevnu5/l3+vjxqGfqqDGb5mErmqzM7%0AoQ94Z9jv9zROk9IGaxTWOSg8jvs71X6/53Tqeb7bC8sVzeXZJc+fP8eYPdv1A7FBbWQ3jckTAthG%0AJoP3owCNKpUENou1RxC8rnBA5OcYs+iJGAUhcLPbc+iHOT1XYrEayzBjngKoXJB1DmYs9NhxHMF1%0Adz4LsnQ49D3dmPrea2kkL1VN6nin02mahYohE0d5vmiKspwWJ0YfIMRxaqnXiehUNt+2vRHSoZGd%0AfNU6mkYwmrN1x+XlJeuNjEpstyIUvlpX8LW8PqtJvp8A35o91O5gHTWon8ek/1M6ScsSZsmH6Toz%0AfabLTWh57U4T5UWAfDnLVRsZNSjVTcD3oimklcEaR0qn6f8722LMyDT35GqHMEHhDCldRgdyvb2e%0Au7v6L99rwPl0Bxit0WZOo1UWspYupCZdRs6naVWlJleAnCscelf42RShZ1Og0pRGco6i5q8Q8aas%0AsFF2pRQyKms626JJaAxpCPTHHrvp0BoCgWylvXwicvSew+nIMWRCMgRvyNEQToZDH7h68BpaWV48%0AP7HfDZxKKbPf36Jtg00Z5XuyiYKxJBn1d01X5lfEh9p4h1Ganj1KS3nV9xENHG49/pQhGlq7ZTzd%0AsHYrxkakJscowcdYycyMddjGMXjhe9hVh0oOE+TiD54CdkKICqNbWZxBBLtbvSo4QpRgqhSHU4+P%0AipAbfIT9yTIMmZy1zPYMGWUcKjpOHo59IPjEGCElTVS1yyIncHeUn621mEHRjkWe4hTprl5wGSOr%0Am5btesPbsSHHyMMLhWs06BM5e7TJ6CBzZUqB1hJgkilgLGIfrMpAopJBCXLJfmpn5/6RCIJjaGmb%0Aa5VLeeOp4wwpi0uDLtWURmGtInlPzGJSp7Vc55mMMRp/FkihCKQdRpzJnHcNp5sD42nP6dBz2IFz%0AHY3pUFlhtQTSjOBoufCePJHBS7Zn1YBWMqgpwue/RbNISqnfD/wx4CeAt4Cfyjn/pcXf/0vgj957%0A2Fdyzr93cZ8W+A+BfwoxafvrwL+Sc37vk7yWOeW8Wxb9Bt/Hx9623MHr7XNn6OU2n1IK5wxazydh%0A2qlIpOFETpHh1DOeRsZ+YOyF0JUjRYc3sXtxw6hHfJTyIBY5Aq0UXWN58/U3+OCjR1xfnXE8HuV9%0AR2gb6RTF/oTWhYcDYgiXi2ZL0V7VWsYKrNXE4vfsWk17thWRplZkJBU304IhI3a0StG16ym7s7aZ%0Adl0pQWJxMpzFtSuOkZOUYdYYjLYiIyC2a/gxMgwjfT8yjoHxVE3ihOQHI2MIDEMizp5z/Njf86Pc%0A3t7y7rvvlhECBSrjY4IBTv04TSWHZz1d8wQHdG3Ld87OcQoeXp+xXrdcX3W0nWVzvqLVNYNgAqKd%0AmifFl+cd0pTB1Kxiea0ss5DpetU1k1iSDmclQZPvNSVyNZib6ROxYICjSZAUCosxq2IKB5sNXF2d%0AgVqRGcnJ4HMS65s0y26ogvU556QrVSQ2UqwuGyIX4cffujb1BvgF4M8Df+Fj7vPTwD+/+H289/c/%0AA/xh4J8EngL/EfBXlVI/kb8HTvIcZCqANaEu3/Vxy1bkqzpF9YLQi/vVY7apkItNQME8SQrUXSwW%0AuYMYE8RUVPUQVbMYSWH24Knm9ikHdNbE8ho2mxUhZt76zJvc7nckFF3XsEoRpUYS0DrJkDTSGTEY%0AqRtixroOkYkQoXBrMs2C7GWtxWpF21hilpLBOVcW7V2O0dzpSFMZURfSx3Xe6gITbZgyd1O6FNXY%0AfhwDfsyMQ6AfIiFIW10poerHnAlJIMiCwPDwtTfIaGL+NUKmWMQIOU1pUQlUWoM2MsjpC84yDNyk%0AA41SdMVcvnGJGBs5f12R3yii35m77Fy5Xiov5m5Lum5Kr+KyLK7Yl67BZcs63ZtcFpA9S7ZR7lex%0AmAgYLBS8bcJ8kDLINYrz8y0pwXGM03kaR7UIbhnnipVvyQCbRkSrUpL30B/38Py7LqdXHt+Ls+OX%0AgS8vP5xXHEPO+cNX/UEpdQH8C8A/m3P+2XLbHwG+DfyDwP/4CV5LudAFWBT85BUB5hUvcxlcXoXe%0ALz2BUMv/NRPmgGnXCXFEa+FytAZgUy5KixotRkEyhsZYWmNJ1jFkw2noiR6c1vTjEeMipnEFdG1Y%0ArQ3N+jVWqz2mcYQw8rWv/W2U1mzXG1pneXpzxDjRUTU6YYhoZHI4m4zVDTlHFBprDV2j2XZaMhkD%0Aq9aw6hqa1rLzI1pHnGuxtpFMqgTSGOV2CRhO3CydKQFWQOJhUExKd1qz2Yib5arbFkBZzM36cSR4%0A8D5zPIwc9p7TaRRyYJALu56+mLLo5FRHyqZFK8Vf/7n/RYKf7ug2Imcw+gGdMyopWmNAGYxxbFrL%0AeOzJRfhqOHrceoUxDSa3KFq0anB2TUoeY0o3ZlXnyeR/GzOzcetRs9WJwvAxG1K9turftJ4HZpft%0A7pczZ3kOW0YLpMSU27xPGNOgkDJ1HAPPXzzlxc3Azc0z0Cs+985n0aphLDIQWmsaJ3YtdQOp7wNk%0Aczk/FxVEXbCYp48+4ps//bMvL6Rf5/jNwmD+AaXUI+AF8HPAv5NzflT+9hOIHl/1pSbn/B2l1FeB%0A38crAkwpqdrFTWflcfXx5edPRg76bgj6fbT//pdelEsCwomx1v3nrTwYoxRWmUmbZtrhpotVMfYj%0AaMvpdJDhOh2xTcN6s+H8/DPs9keury5oGsvxODKqE0prri87dsee60uRdcwRiJkURDFeFcGhxopW%0AzXrl2G6FUl85HyCiWsJUZaLPVzXAGfTMJeuJiLfTXZp827YlELnCSTlnvV5jjTB4fRR+i6r6u0GI%0AdjFIN6foeE1fM5ewDjVqGdBEMZYdv3EWtCakQMyqjDAAxqKsBWMhJnKqUg2yQ6+6NatmRdNYjDIo%0A5aQTpSPOGJxRWDXLelSymgDWhdu0OM81wCyzvjqbhFoGkldfd1NppebsR2uRcK3BZ8qgCldLK1c+%0AM4UtLgif+cxbtO2R9z8cSLlls+nIWWPtRnyfmoaLiwspscaREOas0zlXzO02qCzXAcDhuP8Nrqq7%0Ax29GgPky8N8B3wJ+APj3gP+plD8D8CYw5pzvJ1wflb+96vjjwJ+8f+PdLOTXK4jmUqqi8MAsGXgv%0A2NxxJuRu9pJSIlcRn+rN0zm0TnfG+sVTSHbTGOeJZZKQ4hrbQKNJHnKUmRjvB/rxBPsdxrVcXl7z%0Azg98gbPtBe+9/y5nK8eP/c4f4jvf+Q7PD3B5fYVtG54+f8bZ+SXr9Zqv/d9/C+M0bzx8U8S1xxIE%0ATcLozHrd8c47b/DGa1d0rcGSiH7AF3N3gO12DcyBw3tP0wi3pB7bs0aM5pi7TPV9xxhZrVa88cYb%0AonurtqSUOPYn2rYlP32OD0ee3+wZBnHjFAnMJCLuWoIbuRLxIlkZlDJEZBGmHCFnTv1cgStjyUo8%0ArVJW+JAI0dNYA1Fud9rwhc99Hmvg+nqLIpPzKHiUaXAuCv3euUk3yDVmugaMUdgix3oa/J1rp2a/%0AFextW8n49LIpkysILN/lmlkMFWrKCIDoBdtCtPOLLGkqkaIA8PVomoYY90Dm+vqChIiekRX74ch+%0Av59E1pVSPH36fBpCtcXCVisLVgSoVp1sDLc3L36d1fXq4/seYHLO/+3i168qpf4PJNj8IeAvfpeH%0Aznnoy8efAv704vcz4D2ogeH707N/1SE7R3mBiwvp1YDwy5OvOWdRs68dLi24QLXgyEkGEFPRdb05%0A3MwAopfd7zvvvcfZxY44DmgD203Hm2885Hd/8Ue5fHDNz/zsXyP4HmsSrz285LWH5+QQ+dKXPsfF%0A9gyVGjKR02FPTCOtMzy4OhN/nTgS4twluK97ssQS6gKr76tpZ82TJQ+kgrxC+OqKan9XFoa0uden%0AE89f3N4ZLqzCYehZJ7l+lnNGKVyg74bq38k4ytfp0GNUQqcITtE0lrYxrLoWUbwqQL0Bq4vCXJaL%0AUitVNHTU9HmnAAAgAElEQVSlrLHG0jgZHEzcxaSW+F3lPgETcxjmPLtmv3L7fL2oxRjDEji+Qx+g%0Afh6m4EEaVc6hMRLQYoyMYSD1e1KC5wfhP+WcuXmxE1zm2BfNnSJEXt5XPxwA6FpRPjwUL+5Pevym%0At6lzzh8opb4F/FC56UOgUUpd3ctiXgf+5sc8xwBMY7ivqnGVUpMc4KswmJpiThfqx5RHy/tMX9zF%0Aapbl08R7GDNa1zLCTdlSDEWiAWG4GmexTYMNEdMkjGkZxj05KdyqpYv9NPT3YveYx48t3/r2u6zX%0AW97+7Od5641rnlo427T87t/9Ozkej/zwD3+O64e/i3feeQetNf/4P/YH0CiutuccDge+9fVf5XQ6%0A8vhxIuUGQ8YYT+scMfQopTnfbnHO0TfjtDiWn0ldRBXAlsUzEuMWmAlnokcbJkmH9XpV5oIEl8E0%0A/L/svVuMbWt23/X7LvOy7lW1d+3bOT7tdnfcF7ftNh0UASFYgSRIISB44SJAiXgKEg8REBTlAV6A%0AlwQhhfCCIgUh8RAJeAGkREiJEBECK8Jx3I47bsfuc7r32fvsS1Wt21xzzu/Cw/i+OWfV3qfd+5hY%0AdNtTql2111q1aq61vjm+Mf7jP/5/pSLzUwUqEKIXSxHXo5SUVSZ4os4SkpD1XCIiLQHI7NOtGJPb%0AS0IVMMpgkiWvaAn3MjGiHPfvXXLv/prSRh4+OqMwCq1D8iKq6LoTbXei61uKPrkaUBOjH4cDGQH+%0At63FvEZyt8b5ESQ3OmtFj3KgSo3dyb6T7CKPHugULFFvbnDiJpUdB2SuLH9ex+OR623L9U3A9YGr%0APan7qAbDQp2+xyCgdsY0VZnsXxJW03fTKfgf/PhHHmCUUveAHwM+Tjf9HaAH/gjw19JjHgNfA/7s%0AZ3j+tIg+fUebYimfFlg+7ffGAPPmfdNdy3tZyNk0TYhTEEPAGCu7jFaJ5j+yNHOrUhnJbtbr9a0W%0Ar7WG9tRyfWpZr9es12tWiwUhBF69fIYpLH/ij/8x4QRZmVupy4rT8UiIHcY46kpS5M26RKlKgEoC%0AbdsQ8RhlB63erIE77QgBCVtQFKmN6ZzCuX4sASaaJtNgk5/LVoJJ2KCTd7aIO4WQSWekABLI9rzD%0ASEHKInUMImUQfQo8d/km6fFpoE9M8yTrKcuS0B+pKsv5xUpwKRWxBYK1FDkDG7MP+b+8/rK0wybl%0AQ0/fp1GQeHtEQGt9S71uJNuNIO/dL3ncbdwOxkB1N8DcYv+mzDnjOnLTOLjZtQKeux58Z1HyBg6K%0AAT7Nd2lVShIlcx7ExAdwygmN4vtcX9/v+Cw8mCXwxclNn1dKfR14nb7+E6R9/THw48B/BrwE/ieA%0AGOONUuqvAH9RKfUq/c5fAP4e8E4w9dt2jR80g/k+HTDSeQ5BRLREbmcxg0lYymCkxhZNk1MhAtZV%0AaTBKDOGUhqAN2AJT9BhXgFK46FGlxTgSgAqRLEA1p6pqHv/ke1xdXbG9uSZ6x8XFBVprLu+dUc1n%0AaOUw1vLwyUNubq5w/Y7CQtce6U4NIeywNrDZSBdCJabycrHh3r17zGYzHjx4IBlML6lx7qIdDoeB%0Azi9ukSL90PWyMy+Xy1vKfbmjkoPLCBBLin3qWg77I1fXr3BOAox4M49U/cIaicApIDsDOspIgopy%0AscrFdXfRpwtTYjk6jFSB6D1lZXj/vYd84Qs/jnZbLh9csJhZUIKV+RhoTr3QCVBEPC6IVESTAk1R%0AGKy3gzaxT9lIDqo5wEyDDAi5Lr8/KmdkcQLaxlEJb1qm5gFZAD35G9lVAC0boHCGiuHvSLA3gB5G%0AIXwfUFGj0AQnQcmaIqkVarTSGG2IKhJ0mnoXSIjKfjafpM+Swfx+4G9O/p+xkf8W+NPATwP/NnCG%0ABJm/CfyrMcZpEfdnAIdkMJlo9yfjZ9TlG4LLpxy/nQzm7t+Z3ve2UYLp7hGC7NQu+IF4nRejtgaM%0ARrnUdTAQ+p4svpS/nHO0XYPWmvm8ZrFYDAGmKA3Lec3NYc/6bEXTHJjNZly9fAEx4poW53pWy/mt%0AhZzP3znHarViPp+zWq1kZ+zCUA5lKn/GSKbdr+kQ3rRlezd4j/T2N3GrzMEpK0tZytQzQDC5HSfB%0AzGqPC0EsPj5VSmDkjkw/k/y3fOhZ1UvW6yWr9QJ3OHKxWVPXmogh+A58pGfUz83ZS4yReMoZyB3T%0AuiQ58QZGMuEDxRjFPO3O+d3iWumxfR3iyKWRLtJoCjisw7et44TBKD0RulJS+ih1Gx80xiIjBKJA%0AGEJIZZKXwFfkp4xJa/ndOrT5+Cw8mL/F9+8H/7Ef4DlOwL+Xvj7zYb3CKIP3o0tixA8arUGlQbXJ%0AB6OUwhOH+lwy03FBmlSy5MHE/Dtd1w6DfjEKeQ3liCnFDMoKzVvPsdWaEGqMmUs2oj3GapTOIkug%0AHSh1DSagi14mgqseFWvm6xV931Onlud2f43WmrN7a2azEl1Ie1j5Ld2xZVVY3PYF5Vw6P2elgIah%0AqAihQNdmYLTGlEJ3Xnyf6kUleiKciGiZ5bGG2UywldVKWpsff/x8CHgKg8LQ9VeEuASlh+E+FT1K%0AO5QWZfzgPZFI1yevayct3lIZ5mXNk3uX1NQc1i2vX4nB3HVzIqApywLnI11zQnmoCotSmjY9V/+G%0Ab7jgNN5pWueZq4oYI2VZMw89n3t4wQePLynpuHywoaoiTX/gcNjj+ogpSowuCfrEyY3dMat1uiCh%0ADwrfeWzSWCl8mukx4yVRUIxlZhJ58nFcf9oiNq4qazPLO6pGGwQJAjrJWmQMjLtllYYWVOFByTCC%0Ax9I58L6gskuWM0Uza+k6x66qkr2KJ8Y8tydqe4VWtzYGH6x0u5QhRkUfPtPe/0M+i/TbOG5lNZPb%0AtLpb17/99/Jxu1U+OgUMdHqTWax6qJkzqxVtUMrd+n2t9NB5gbGmzzt+Bli990T80FbOpvZFUUjX%0AJqXZMUasLQecZ8iuOkm582Nz4AzRobRoqYhId5kkAIrhPLSWIcHmVA3ZzjQ7ymn8tOM0ZnV6eC0g%0ArNHLy0su0azn1xyPR47fe0rTnOh7hTIWYwQ3UPIrMn8WpZuTn3964WX6wEAhqCpi63n06NEwW7VY%0ArDidOnrX0LYd3kV0iGjlsXrc6fNg4xTUz19KKbwRgLtQE5YzcfQ8V3ny/c0M+6541ZDRTHRbhOiZ%0AfL6SfEYGhYfHJIwqBsmWxfIm0nU9p1NHczylAFFJ0IipPZYm24kyYyVPmCgcJqQ0IhMnf4cwmP8/%0AH3cB2e+Hs0wX5PTiCHEsEcYU9k1wLsO1SkcII8iZF1/XCaekmM3Ep1gD3km3QIt3cVEUMh8EqYtQ%0A4bpAkYJLBlqVNomlegIV6J1o115cXFDXNRcXF8xmM+7fv3+L6JVp/HaiZeKcw3XyPunCDhdQzkDK%0A0qbSIFDPKrRBvJdiwHsxmZfuhuLy8nLAHnIpNab8Y/s2RrGJPZ1ONEfR5u1SOahQbDZnLJdL3nv8%0AiLZt+fLP/QyvXr3iW7/2bXbbA95bvI+0vScqT1VYvPacksZKloQoEha0WAh3YzabDfycr/3UH+C9%0A9x9TlZq6lA5LezpI58+Jv7dyHq0sizqvh0hzbGl1P7oq5rLDSpkS1BiMpt22t621fPvgwJACfH6/%0ApuMleS0JSe/N9ZwzJG2ljPQR2tZxc33i+QvPy+cnnj59zfX2yKlNTgxRk4ctQqIrJn8TQgLMVf78%0AEngsf9H/nuAUvFuAyffffcxdnEDYkuaN3w1hYi0xkZzMI/5jTZufX0sHRDHsPkYXeOtRqhgWmNb9%0AkI3kwJcV65UaFdlijJxfXLDZbLh/eSlZRl0Pu20WgpasKL0mGCZyMXpU3yuywlwkRuGldF2HUkqC%0AQtPiQ1bZH3lB+Zxy+aWUSsEoTt6nEQjPntcxKrpOLM9Qioik7bO5DBzeX29478kDZvOK3/jND3n+%0A//wDyhLKssAY8V7uuo7CjAbzmdSWX4dSiv7UUBrNw4cPefT4HsYoZrMKqyPb1y+IoSPSDVKd1WzO%0A+dk9nDu+0QyYiolNLYqna2+6bu5mxnc5MjkQTZ93eL5P6YpOCaL5u4sBrfJ5KpwH10d6BxgrZEXl%0AUdoOGVWOFUExelTHibSJuivWoIeS6l2PH6kA8y7HdMfJ/58uqHxBeO8prHlj0YToEE8f4bjI/YGu%0AcwQPChlgtLbAmMyZIE0VR4x16KLEBtBWLuyyLFHRT4LNGGTybqe1mKwbY5jVi4GOn/knxhjquhbF%0AuaSP24eEHRlFiIpopaWtrUEZWbRZj0Ub2a1DcOz3PcfjaMRWlGYYAYjxyPHYDe9hWZa3spgcZJum%0Aoes6fAyUdcXmTOP6QNO0uG6HVobCRnTsqJOYt9c9s8WcP/KH/ym2+5/jp7/2Lb75K7/Kb374lKZp%0AsEXNclbjw/xWIMjvz8///M+zWq34hV/4BXa7HRdnC5pmz/2Lh5RlQXfas9sd0MrTdkdUIjl2Xcer%0A1y8o1FjGjiZnDJ+xLANpaWOSxcukRIqI6byIlyEiYV0/rKucveRMczqnFGPEVOWt9ZlX3S2xKJ0F%0A7QMuYVI3N57nL7Z893sNNzdgixmzuWV3PNEnLhYksqMS76fWdejkR6VVki8B8Im3hLhGqN+NvkjT%0AEmeo+ycpev55GBJ6h+fNOMo0sEw7BFJSZJ2ZN3epcTxflOi1lp3v1IsJlkoCQbGMRNejlaXvPVVl%0AZFdXUoTF9Fw+RnrvKbTo3CqTFPuJdN5RGo0uLLqw9MHjvMMTpeQzesByfAz0Xkzg276jqEr6znHc%0AH1BKUc8E4DZmFFLqOsd8PkcrO7y+9XqDtcXgCZQzKxg7aSDlwOl0oprVclFhcCYN1znBC2aloSgU%0ACkcMgbqcUVhF3zVUheKnv/YVzs/PsMX/zYff+S6vb/YYPWdWicDXT/3UT7HZbPgf/sf/lYvzGb/6%0AK7/ExcUF0besFhVf/IkPqM2B588/ZlZVA8ZirWW3F0r/ej3DFFZsVcw47pCzxrZth5/z61JKIebz%0At50tJECHW+/DtPU8belnmYspiXFaYmmtxaZEqVvSmTmIozW2LDidOvbNUcYklKIsCz45HtntjnTO%0AYQhgFBZwzmMKLXSFpMUcekdRVTRNS2kL0WkmlZ9RJTLfux8/1AHmH8VxN8W9i9WMi8PhfY9zYlyv%0ACzekmfLhpy8X8Tpgo044RhTFuQBRCSfBWNklVSTNudihhTtNoXOL25hq+NlaO9C/M/YwmIKlmZiQ%0AeDUhCN7gvLR9lVI0jYhd996l7ERU6k6nDqX6xJjVFLYmtzxzkLHWikFcKoveBlhmPdvBnG5mYQbz%0AWcWsSOS1CEZ5oj/hPZTlglkZmc0EYPTRcPG1n+Dycs3V9ZZ/8A++zfNPXvLxR9dcns159tGv0+7P%0A+Wf/6Z+lKCTohXbH1770eeq6JvQHXm9foFSgOR3wXUt32BNcjw89xihe9VeopITnFemcUwelF9xC%0App9zgBizGobSXKG0xnkv4yBaDxouJt4ue6ZA+JQ/I+/fuPYEhE0gunqz7NdlRdt1dC5wbHo+fv6K%0Av/+tpxwPmsMhgdNaPofgOnSRO4UJnPcd2jq6vsPGHh8bumAweiOWLFlCJPxeifT/yfG2wHJ3YSil%0A8MFNHpNb5KPPTd/3tCdDYxtmC/EMkjGcFDAGXEfjfZ+EqANzM5PyStlB5GkqVkTUIu040f+YdnHG%0ARTpyXYKJos+X62itMIWlbzvaGCH9vlD6LSEGnOsRvEU6FjGNOYsPkJSIU5O56QUzlbrItws9XtjO%0ASilU1FSVDDNmFSmVCHTWKLTyEB2gURqaw4m6NDy4vMDan+TBg/ssymeEEHjx4gUKz2o5S2XNiqIo%0AWC5k/umTF89Q5oRB0Z6OuLZDOYfve4pSZCYiogpXVRWF4tZru9sRu9Uc4HYnMT9mqt0rljVvrqXp%0Amrq1/u5kzNmxIrOsp0cW/YpKczy1NE2bJFK9zGwpg9Y+qdTJyIQEwAIVoagNdWlRKlBVBbZI+FXr%0A0Dqgktxm5HdhifSP4hgXkr6V5uYdepreQqAoTVJmk9u2N3usNhRR6NZlYTDFuGB83xOcF1EpZYlG%0ASZqbMlDnQSxMHV0v53J+fo6CoWRZLpeCVUTBRzbLBWUp7WTpOsmFsVgtMYXl1U5GvlzXJ91bBz61%0A0ZMCXp2wBinzRcfGe9GQ0VrTngTPqapsiesIsZlQ6tWAuYQQbgHTVVVRzGZiRev74Vx0JuGFTFeX%0A97g5XNO3lq5vKGzJfLFB15pjIzjRvLI8fHDO4/tPuLq6IoTPc319PfCWnDtRFppnH/8G+/2e/X5P%0A50/CiA2RwijW9Uw+p0LkMUPsh7a9b08DfpUzr8VicSuwDC4Cxe3xiLd9wdgRzOtrytqdBiPhEo1Z%0AYMZ0BCOZbDTpuffHhrIqUMahrRFpj01LVI5iJsqBi2XJxcWa2foeV1dXHA4HSmuxpmA+m7FabtBK%0AibRG4j999L0P2e0OfO+7n3A6dbjGwendr6ffCzBvOd7WBYA76akavXAURmw+UldgWr4URULxGduZ%0AWmsII0+DmNrcBJQ1b5xH0zRYa5nP50O5oZSisGOtP7Q0J+drrRUJxU4IZ33bCTO4bfHOURdjFyYH%0ABXzeuVP7MuZMKPskCVnQuzg4HeTfz5PRObPKF+h0IDBnY9qIfo7ODIwo3TUdc4DtiEeFKx2mKAlR%0AyVBk72g7l1rqNfOZYD/Hww27bTOMNmxv1Agwe49Tnu50YjGbi/tmUcsktRKtHJI0Ztu24Ea+ybR9%0AnF/Dra9s42pECiJf+Nlfy8UgnlF31tPd9TWlRqhJtiSZafpbRr+RwRhjpMw2o9d107V0nXhNuehZ%0AKkM9qyhKRVUbnDeUCWObzysWyxrfOxENs3Ju5/cXeFqCOtKHFq9+Fzo73m0pv8uRd4epax6AR7IL%0AgyLgccFRKJ1wYuE/BBXoY6qJg3giLcoaaxQP7m0436xZLUuKQlMvLZUu0UR618jvEelDR7BiJu+9%0ApneOqqiJesRLXCcX9e7YMJ/Pqesls9mMuhY8pKznWGu5unrF4XDkZnszdIC892w2G6pqxUWdAEoP%0AexSHmy1VNSNGRXSR4CK60NxcXVOtXJL9rABFc5S0e7GYobWm7zu0Bh9aIpaub7G2YNfIrn/oe7pO%0AfvZE6rpiNpuxLAqU1pytzgneczzu0fWCGDyu7YTxm4hkRVUktwYRtN67HVVVUXrAw257EP8kXjC0%0A5LsT7f4l7nTCOQmWXSevJbgeXGBdz6gqS1loipkmaE/0HTFEEfEOmu7UU+pInVr+tkzzW8YQgT5K%0Aq74wIgSVrWRzENBpbm0gViKlb5SxHmkNx7FLGZInVhYe00oRkvtlBByJU6S1dH50JJA2JGMobQvR%0AUanI5x4/oTYzDtueFy+3PH16xWHfUuo1m/mK+++f8TM//XnKsuRqe0PTNKw2a6y1XO+2zGYl2SJ2%0Ac5jT+iPH7oZds0fxOzeL9EN9TFvR09vu3j9N+98GcOXfyW3b5WJJYfUtYHZoM0bp5ox6qeM4ggC7%0ARdJBLTEFZEOyWEW0sqyWElgu7t9nVlWDRkdRV+l5ZJReTM7DwO7NAK5yI16SMytIJRcWFRkM3too%0AQlGLhWQxXScZjzB+s0h05ppItuW9p2s6ju0Rk8YG+r4fbEWUUlSzehhOtFazXC7RPoqEpW3xrqNv%0Apaw6JS6R/A2IcdQ/ViqK3onWtMksLXOP8pF1kVcrTZmcFrreY+zoliiCS6LyJ92gkRyYTfWma2HK%0AfZliX7oY2cTDZz2ZURse9ynrcVgTetTWmZadd0eA7m6k0QvTF0bJDNmEkjuA1SwWC1arJY8fP2a1%0AWlHXNYv1iuvra7b7HTGKkt0yrTOtNd1eJCPm8zm73UHK6s9w/EgFmDGTGWUWpgvl7nf4/k59cJt7%0AoLWojM1mMwqdFkZ637OnT1NaqsKyXBTDgrVGjNgjBaHr8YlR2/c9fdtJZ8k5NNe4GIbS6t69S+aL%0ABQ+fvEdhSkxR4qKmTeVQezxgjOHi/iVnF+ccDgf2+y2vXr3CGMPL169QSvH4/hJTlMxNgSpKDk3L%0A9fWW4KHzPRrFi6fP2G23zFZL5vM5odeIwp7H95JN6SS4FLT8f7e7lovBaLbbHW3bcOpEp/fs/Dy9%0Az5HKlMxmFVVR0p1OvHx9xel45MHlJQZFvajR1LiulWDeHsWj+nCicx3HpqGu5xRFhTGaqjA4D74T%0AvZ3ueCQGqIwmGunGWGMoi1IKMK0IhWilaMQDSGmRMQUp04zNk8pQmnLgCOVjEDe340RzXkt57eW1%0AdNf3KAewYf0JdZsYI2VdDZPZp9NJghcRzIjroORcQwhye17valz3xliquqC0hlN7wLsTXXvEFpav%0AfOkLfPFLX2J1uRzO83g8st1u+fa3v81sMef8/Jzz83OWy6VgTvdqzi82/OIv/hI322t22+YzXZM/%0AUgHm+x1vCy759ukh971ZL+eWZF5cGVDtneyefXuE6KkKw7weNVJCCEStMdZgo+XUSkrftq14MZ/a%0A1NL24qmUgkvhPOu+F2PFqHE+iHF9jGRB7boaqf6ZZ7NcrjmdTpPZnyCEby272dwYVqsNh0OD7wOn%0A/QGrDfv9ga7tsbWjbTshomlNYUVCMSaZz5i6Pl3X0zWt4AtK0bcdfS8pv4vQHvME+JyyrKnrmrqs%0AaJqGpjmy3+14cHkPMnagJTMJIVArh/ciNq7arHbnCEEkM7WJFFpDGoHI0hl5fqvv/RAsQEzq2uaQ%0AsivBzea1eFYJU3uc5TJEyuo2PSCQ+ChmJD9mL249UaK7+30aYEL+mdulfb5/uiF6JbNLd5/LM96e%0Ag4u0sXUqm0Q5z+qAsaCUp6gqNpsVy5mU1afTiVevXvGd73yH7UEA8Kjg7OyM0tgBx4lRukpnZ2vm%0A85qb6+1nuu5+pALMu2QwU77GdEeatlpDGMuKzPbMDM/9XiK6UXKB6MKgVWS9XlPX9fC4KUiY/34u%0AU9brNX3ViUWEUlhd0DP+zfXZPRbrFQ5NDJG2EYvVw0n+dq1ESOnePZlFms0rfAws1xua5sB6cw6A%0AtjW2nFNWlbwWXbLbN3z8vad88xd/GRXh6vkr6SKFwGw2Yz5fU9iS+/cfJGW6uQwdKiENtm2DNQbX%0AdTjXcf36RnR4lzMOuyPb7Z7NZsP7Tz7H2dkZdiZmaqe2ofMOWxZUadG76Ak+4JKpmyosVaUp0vTv%0A6dSJ9KSH4B1FIXq97hhZ1hWLqqRtWxalqK+17ajK13UddT1ndbEcyhGDGMFrrQciY12Mkp9FOfEw%0ASsGgTJsGKavJXaZ6PpM5nRhHfWedDf1GD6Ps0z20tVPAmE7sG6XR1hIIA+4ylEqpRZ0HKUnPE1zE%0AWEV0jsIWXNxb8bNf/yovX98QomYx3/D4vfsUJbgQeP7sGd/85jf5u7/0Syil6LyQKLuuYz6fc3Fx%0AIevERmxR8qUvf4Gr61d89OE7WZYNx49UgPl+x9uwl9/q8SAfokT1pGaWMoblcinYgpGLtjAlWkVW%0Aixl1BgYn2c4AYBYFVgkOUdUFp2NDJq8RRH5C2tGFAJvJzBzAo2T2pBNiW+s6XAyE168pS1GDX2+W%0AGGvAWOrFPI0OWKp6JuMBiQkcAhwODU+ffYLygdfPPqE0JS4E5vMl63VPVc4o7Sydf6rxtccYAXup%0AqlTqeVwfiASafUNzalmtFyyXK1arNbPZDDvTCasS07iu64ahTgUDuCgXpEsXmEwmmz7ZpkRPjD51%0AoCx9bDFGRKC818TKDsS+EAKnUztkP8aUhODFvzvZpOq0aci84m2mbVRq0ONFT+aGGDuBUd1eV5+G%0A7+W28q3b0/egGCatfUjYS2GGbhTIyIEizbFNn0Ml0W+T2euKWVmw3szp+57VcsZyNWdeF1gTiQl7%0AOp1OA06XA+XN1TXbrchlCB/KY60Mji4WC/jdOCow5agAw46UxaPzhzhNNe9iL7nlm7+LTUNgPp+z%0AmFWsVqskC5mmrb3IREbXDOCYUtIS1SqiCURfUZUCSM7ntWACWjKXro/DMGFzOuCTVYg8uSJiCUWB%0AnSf8RpuBhj94Tqe5o5tXJ7q+Y3fYp3Jkxu6wZ70WlblV8rZROuBQKK8otGW5vqCsFoRoePr0E5QL%0AFFHRe8/Llzdofc2svsLakg//4cdSjtU1qJAu6ILFcsaDx5fMZrNEea9omgOnvmG1WvDlr/w0l5eX%0APHooGZC3Dr0QXGe+XBFjZF5XkpEdxaN7t9vJjNWswCqNVQZjFct1yXF/EH/qU3KN9IG6LocAkv2Z%0AMjBsMBTlnNVKcIeWBpGKSFlGesuNErp/SGQ4YwxuwnvSVjo7USdNZZ0wkWQTEGKcWM9MeFTpPpfK%0AVB9Hc/rKjD7WKgpGpCLiHS4tKDk3I6JkWouCXc6I0WoIbjbxlbRC9JWN4eJ8znI5Q1vxeVqfzfAu%0A0jrPYjbnvcdP+PVf/3Vubm7YHw6YpqEoCj78ze/wlS99WSxrlyKktdmsee+996jnc06fQfj7hzrA%0A/CDH23aPadmSP/SMnhdFwirmc6pivLin6mZZQjKEQOgkyDWHE4qAvX9BaW93bLJw85RXkSeQySJD%0A6d8YItYYCmuxSmGVIvg+qZRBWRhsofGu5LBPOFAjnsKna5lHCQoWixmLhZi/zcpaOgO9xwch2rk+%0AcH5+j/l8zml3JPiAT2ZtRGgOLSE0aNUMHAtUQGsoCst8UdOFnsePH6O15tgcaNqW1WrF+uycy8uH%0AbDYbtC1AG9q2Se1YS3sSDGq/3xNC4HDYcTgcOJ1OQhishWXqvZRF0imRkjMYOUdHoKgKlFNYb2Xw%0AlJ4Y4iA9kfVOyrIElzR0/DgKIiJyQs1XYVwjQ7ZiRiA3i3LfJdC9jR7xaQ6XGWB1MWC4PSqAVijU%0AAOrmciwDy3nd5iFHpTKzanoECAGHZlbP+eD9J/QeiI5IIEY7eCLdu3ePruvYpc8AH4a5srquiclN%0A0n0wBboAACAASURBVFopj+uq+r0AcxeQzRhMDhJVwiDyhT9F/vPUbA4wwvnoubm54bBX2ES13e9u%0AOBwORCdyklELmezi4oK6KtisFqyXCy4u1mKNUVUU1qJiwPlxcUwDTEhjBwC4Ht8ETtHxOgaOhx3L%0Aw5aimqWFpqROD4Gzi3OUUux2O5qmYb/fcn2zZX84DBdWURoWM3EMODs7k4vNC/Bc2JIvfuFLPPvo%0Ae3z069/Bt/3QAu97j3deJr5tgUhMBPr+RNv2HA5Hnt9ccXVzoKgsq9WKi4sLfvYbX5eOxOUDjDEc%0Amp6uO/D02XdQVlL0b33rW7x48Zz333+fe/cvMMbw4tWOpjkIY1alAJ0yuHkt57BaLIm1py7rFKBu%0AwIApDTpKdyaEJHmpwPWO0AearqGsFEaB2D4rbNKE9GnOyBuPihprLKacyGLoUdMmZxHT8qWqkn1J%0AJhoGfzuz1iI+bpK9ySCXocTULYQw6NlkScyoBauxk7WilLrFycnnEKNGpWn5EHopoyL4oJnN18wp%0AafteKOJe1v9ms+HHP/gcvnc8e/aMqix5/PgxD+9fytiGDyhVAJqiqDg/u0c9WyDS2u92/EgGmCyf%0AkDOXDKzmIKImt+ef864jw4txZNYqONusgLFN7ZwjGvH9Wc1Ww5Rw5sFM2at93zObBLMxCEo3yWVC%0AWQgEF6EVTkvbNcI/aST7KJ1D2xK0QhcpLdYjmFwUxSCw1LanRDTrBvwkO/bFIJPAfSeiWMvlkuVy%0ATV2UbI89NolYh76X6ZMQJYtIuq3N8USIHq0VnY88f/EJi8WCe5f3uf/gkvN7lyyXcyIKHwJX19dc%0AXV3x/OWrwYZVujwG5wIoS1lV1LM5KEVVz1htziBE2mND53r8tmezXqO1RVmDMe3IEdHCcCVGVBBB%0ApTApbwjCN3K+H3E1zCAUJRtMmhPjthZuzia01rjgR+OuSVbyaZjLtLmQHzd9XgG38yjAbWzl1trU%0A4/fpOQ33x/x3kwKdCmgjzgf4DpvKLZJbgkFR2YLFYjEIts/ncx48eDBoPef3QKWGQ13PB/XAdz1+%0ApAJMPu6Cbd57bNr1M/6Rx+8z9T5jMNIOFZCxKsww42OtThosJYvFAt8Jm9S1ooFSmBJrBPw9O9tw%0A794GayUj6g4HYhoAzDIA3nt2u50MHLay+H0fUG0jJDCtsVVNnUq3sqpQCRRFyaR0NT8fspS6rlks%0AZux2u1sBTALt2OZ2vR+sQqtZzXp9RnjgKb3mux9+hO8j1pSURZqoRg9yBc3xyM2Nx1o4vyhZP1jz%0A5S9/mS984fN8/otfENxns05EvTnKGn7lW9/iV3/1V1ks5mhtWa+X/MTnv0hd11w+vC9dt1nJV77q%0Ah9JmMReQ9uOnT3n1yQs+/uhDttc7whPPrKzQylLYinKWMBiVpCx7kahQhSb4SJ9EsoIC5zpCci1Q%0AIXKKMiWuMgOXzG+x9K0beC+5a5QnmVUiwQ1rTd8ul7TWtG17a5rcJBbw0MVUEBJBsNBmCDL5/rwW%0ATTFO1efsSVxiJzpGkKQUREJVrHM6CivrIXjLsemG86nrelBBvLm54fLykrOzM9577z02m81YEmJQ%0ASlOVMzabyHy++EzX4g91gJkCtvn/8sUQ6eUBHryjPzWDPon3sqB1WaBjQCVR46id4B0GSELOp65l%0Apmqc62nbhuPxiGt2gt1UkrYu5gVVWXB+seT8bElV5TkhKGpF28gwmtEFaCgKxaxcY0JL7Hb4INYa%0AjTKYWUlE04aAxeCDJgSN6Ua9WY0l9nuiKgkUoDXFfEZZaEJdYAtF30tQ9Udp1y7KJa6Gtu2hKLD1%0AjPnZGh8C2+2W+b017dVeAMP+hIotVhcYAkZ3FCXUS7CVZfPgER986cf50le+ymazYjZfEZXi2HqK%0A2tAGRbNvMPWCB+99wHJmU0erYj6fUxQFm8WSuiiZ2ZI+9vRdT6E10Su0spxtzimLinJWc3NzxYvd%0ADbMg7fje9OjZEt/3uG6PV6RgIA4CUQV0kTCJU0sRK4LrxW8JIOMwmUyno3StdA+FdNOIHpuwElLw%0AyKX1EAzUqKCntEbbChUUXWIZu9bT+Q5XZJqDGwh01lr6mFvcUKayzCvpCBmtBkBXkQh1kwwcED2h%0AILpDqEKSmGjRuiS0PZhIoXtce2JW1pxa0frZrGpW67l004whGGhiT2U9VQUdLUYbegWqhHLxe6MC%0AbxxDyRTjUDLkWjnvDNPsJcZIDNmdUcqAeVVzz57jUxljjKIsCmZWSqO6lHJovVxQlcWEqDTpbHlu%0AAXJBSZo+LW+GOlvXQn6KgiVIZ0WAtsV8OZ5njASvaI7dUJuH1zcEko2rMVSlLIrtbitCU8FjQhjS%0A/qgV682Gqig57Q/0fc93X95AcHSuF1axllKj0DNmxjI/X3P54BE/83NfZ3V/xXq9pmmPaK0F5N2s%0AJIDHUbDp7OyMD957kNr5evgschZp9Ngu1Vpz6tphB1+slsyXcz5nPuD6+prT6cjLly9TZTDpCimV%0ATNnkYhu/54whpspm1KzJn1EeCs0X/jHenqLPa2V6YefPa2rtIhieZMR1LZeWZIyOtt3dMuXLJftA%0A8EtrASTQTEuqKWcLxpGATPjLh4pAsrbNJbFSBu8UIUR2xw6tEz/LQFXJupsvRM/ZlKPImKzYEVye%0Aeo+/y/EjFWCmGczdY3rB54t6KuqUF5TzbihlCj269OUFMKtFpLk7bm8tVOccZlIn56nhnP7+1uc8%0AXihCCBuzsxxwjLZDVwqgSczeOtQoo8e0HjDREJJyW1lXw4UysEVTuWithVnNbLmgns8oErcl9h3R%0AQx88KniMFTnPi3uXPPmx93n46BGneMJYSzxFAjL7lMWnFqv5EGCyMZvWms55cQ44HilKQ9U0eL/G%0AaIbJZ8rMZynSeQsecH5+jvdrAPb7PcftLgGr4gSplSHoCPRD2SDvqRkkLGFS1qSApq3FlMXw3ikX%0Ah0xlunbusnPza5oeUzkG+RsjwXMg1OWyKY4OktNjSvqcrou7XSlgmPe6u6Y04/kV2tCZXIqFIWDk%0AayGPv4iXT7pOojy3QYHSFL8TGIxS6s8B/wrwZaBBvKT/oxjjtyaPqRCnxn+d0VTt340xfnfymA+A%0Avwz84fQ8/z3wH8QYu8/0Kj7lGMC2rDsyeUOnmqhTWn3nkidvVVEl7RUZSDQDd0JIXNJSXS3WlGXJ%0A/Ytz6qocDN/n8/nw3EEVQ6CyZTZNH6UVVVdg0vl2IUseTCfFE0iddsdBsc4pYoS+iygVaHsZN/bR%0AoLXowhhjmC8XA+jtJ1hQnm2xFCyWSxabNWVdEVLAiGh67zDR4p1MR997cMnjJ0+YLeb0TdJ2ybol%0AqcY/nho++ugjwSIULJcy36SU4uXLl7y+vuK4P3B2doZT3ZBB3NzciHYLgcViwZMnTyRjLCtOJ+Fq%0AFIXm7OwCpQzHmwPBM2QPWluMifhk2xGDltZvAuvT2hvWx/Qizhd7voCnqoD59gzU3/3dPPAq72u4%0AFRSmQSgHl/zcd0v7uyDw3bU8/T49sjmaUvJqb59rUg0g+W474QzlhkAmc0rHLOKj6ENPD524T5/l%0AeNew9M8ggeEX0u/+p8DfUEp9NcZ4SI/5L4E/AfxrwCvgLwL/s1LqGzFGr2QE938BXgB/ELiHuEIq%0AfptGbOMHc1fLJQ21TfkncGvyOP9uoSUArVYrisKyWa8pCkNps5lWT38S25CyLFmv1ywWC+7fu6Aq%0ACx49uE9hNKUdFeeyBm/f91it6YqC4LJeygkV00XStnSnQwKkR/uK7P/8+vVrYhTNEmsts/kZSitO%0ApxHE80l43CWsJuMdAKebm/EiypwM12OUZnlxxkOj6I+e69dXRPUxh8OBw/ZAdJ6Ly3vcv7zkq1//%0AGR49fo9T31HMa7ro8TGwPx7oXM83//6vUJYlT59+l1evXgkvZr3mxXNxjvyNf/jrbLdbiqLgK1/6%0ASYCBLv/ixQuOxyONb1kulzSnk2SSRUE9S7ssyCjDYs3mokVtt+x2B+G8GACNMh4dVMrgxFVTI+6E%0AOdAOYyQ+4rzD+THLiPa2Lu60AzjNUDImMqU9eC+0iEyeNMllMcb5UCLlcmuwlRnmye7gK5NAkYNT%0ADkwDsDxCSAPb12Qfpa5Lf19K91lRUYZaFBF1w2az4eHDS9brpeBWUaFM5o5JoFFKMv26+h0IMDHG%0Af376f6XUnwI+Ab4B/O9KqQ3w7wD/Vozxf0uP+TeBj4B/DvjrwB8Fvgr8WIzxaXrMvw/8VaXUn48x%0AvjFVlbKianLT6gc416H3l608cgZzdw4pPyYDw0PHqe85HA4sFjNI7GCT0pjVasVyueT+femEPLh/%0Aj7oqKa2GMAov5d0xcDvNnqbN2bHPp9vlfJODpLWDcdqhOw7WH0VRUJSCJakAMYC1BRbovSO6QOs7%0ArC2GC7jrukEUKws9d10nMzCAsZYHjx9hjGG73SYcZocOnnv37/Pej73P+cV9irqicR3aGBEDt4qi%0AKuEonJzFYsF+v2e73bJcikLa6XRCa83rq2u2N9fMZjM611MYi4+K6PohIJpYDOJaOcA+f/acR48e%0AyQVpPGVpmNVz2lNHiiwoJR5CSsluTO7cApiYPJiBdJFGJEBAKpt00niJ4RYmlIPJ3fWVP59xXk1R%0AFFkOIslNkEuqesAAp2vxbsfzbhk0XUNvrG/gbv1tUmmU/ce1ihgtc06ud2hTDI0OrRkcKCSbBa0s%0AqAAh29MEVDS/pSHhpx2/XQxmk76/Tt+/ARTA38gPiDE+VUr9MvBPIgHmnwB+OQeXdPx1JIB8g9u+%0A1/n4c8B/fPfGnFZONWsjo8aGmqD+eafIF1r+UO86G/rgRVqy7dBGMa9nVIVF27QoSmFDXpwvOT8/%0A58mTJ1RVJfomimSdqjEi7CI7iRMMARWJyqBMgYqRoKS+VcqAjlTVjGomvIQ8Ya2UomlaUaHz/lZ6%0AffXq9SCXUJYl9XyO1noApJ1zvD423GxlcRRJHtNqQ2lsCpiKzne8fPmSw+GAPckFX88W1G3PvfuS%0A0f3sz/1jrM427JsjXoMtSkLsqeYz6kVN0zSg9VBqPnr0iPV6zdnZGYvFgsPpQAQePXo0jF+0bY+Z%0Ayw7Zec+jJ+9L23opQ4siOiVB/vLyMc5FIGBtwFpNWS2YLyIXFw84Ho/sdjfCkDUllS5xOunKhF6s%0AbLXwRoTAKz+71D104bb053QEJR95YjtjYHVd31qLksmU9H0/8KWKJO/QNG4oz7uuG9bkVG8og7/5%0A+afPndfS3e9hulmlQGhtEmVP7fu+PyX+k6bZHzkcjjSpvP3i7/sJdvs93/veR5zfv8e9y4v09wLG%0AFhAtRluWq/lbLsvf+vjMAUbJWfwXwP8RY/zldPMjoIsxXt15+PN0X37M8+mdMcYrpVQ3eczd4z9P%0AfysfK+CN8c6xjs2DJpJyuvh22vYUvc/8lOBHLQ8b9aDbMk8qcoTIbF5zdnbG2dkZ5+fnUssWFmIQ%0ALgsCNN/6e+rOAom3dwRjDLrQKOUH+QEYL7Jcks1ms6Hez2JLla4SMZChBQ8ju9Q3Xeo4SFvVaY0z%0AZghYbdex3W5lIjkuhoVeVdVA0stSCIfDER8i6zOLJ9A5MVDLnbmQRiKWy+UQeKuyRBej/9I0oGut%0Ahy5YVVUy57Reybmlaeg+SKZA+jwiSBAsKqrKY4sKRUsISBdF2eRE6ABh0iplxYUzfwZBUKZMIMwZ%0Ai2Qdd2xD7nQF72I2+X2Wn0e93bsA/vQ58/e82U07Rm/LaqbnMC3fVIzj0GWckEtDxOORtr0mBtC6%0A5HQ6sd1u2R5aMGNnLK+z4VyilF3EgFGK4i3mgz/I8dvJYP4r4GcQHOW3Om4DI28kdm99zPjgGFug%0AHR44iei3UX2SmXj6gId2npk8Rt36ILuuGzxuMiYz0Lcx4OUN1lpT2mKY8REG7DLJGBgIPk22GiFv%0AxREYjCoJB2kFyqBUIOggrgEzxZLkw9OLfYRPJln5nGKMzOdzZrV0ZtrE9g1e0lhrDYTA1ZVgNH3w%0AiYFZU9QVeCnXQu9wvkOFSJ86X83pJAE47+QpoKqoMcpCPOF7yZbq45x9Kzq3VVURZpHW9fR9S+hH%0A0zdlRwqA0dLd6qOjbUQ1erk+w4ee8/VGRLZ9AG04nhp2hz3Prj7BWsujR08wpmC13KS5JcFj5jOR%0AXiiLkr4Qqn/vg/hLF5qu79L6MBhtMVVBpJu0sSNkzKrviaRhxiAZgYmjm2YGQReLxYCJTddRxlHG%0AzaRPeIoVXC199jlryQD7dD1Og9DbOlZ3g9sbwSdMAlIUgiXRJ/0aKwb3SrHf7/m1X/sW3/nOR3z8%0AyRW6KDkcG5S2UCjmqyV/8A/9QfHwroVBHoNkMyH+DiraKaX+EvAvAn9o2h0CngGlUur8ThbzAOk4%0A5cf8gTvPd46UVrcym3c4n/TTnRQyjLoa08dOU+GpTzBkUesREB5a2Qg2s1gsmM/nSSO3HmpvMggn%0A+BhxooSXg5zWo2BVCMIvUV4RrGRNfRjFu3MXSZD+JJkQGMSqpBVZCIagAs572lawmdB39DLPKy3J%0ABPq5UytTw37snB0Oe3wIqKogxEDoHb6TYc6ubWlPPUo5bm5uZKTBakLvaJoWZSNVbu/HgApqUETr%0Ae9mZTSoD+uAJyP11XXM4HAbGq0uPraqKrut48b1PqOuasqxlHGO54d69+7x48YL21BP8HucC++21%0ABEPyCIfMSolyXXLSVAqrzFt3rulFPOWb6DB2jnJAyF23t13g0zUYY/aESjKf+s3sJZf0+f+31/Cb%0ATPRPW+9vBKGc6XhB/AwBHz1G22GNN03Ddrvl+fPnuAg+RLQpOHRHqvmMb/zj35hkWKC0xRj5+izH%0Au7apFfCXgH8Z+PkY42/cecjfAXrgjwB/Lf3OY+BrwJ9Nj/k/gT+vlHocY/w43fZHkQzl77zL+byt%0AZTdF/LMHj9XlG2nmOHvkBkQ/xojV8gGKRm4xgGCy4EuWyyUP719y+fCCxWKRdmAvmalWRB9lfid3%0AJKLwT5gELClBCqL19F5IZ33fi/ZJygK8j4M2R/75eGhuLfzSSmmRuSdlUXBK2Y3So3TjoZH7Qyc6%0AudGHAbQmdZJObUNRlvTJLvbm5oaubTkdBJz95NknFFVJvVxQVDXb/RFzrrm8vCQiSnalsSzmM5qm%0A4cWzj9FKSHYAHcLnmdcVl5eXhBB49uwpm82Grj1xPB7ZbDZyEbQnrrc3vHwle9T7739AXc8SfV2l%0AQNLjWxHgCi4BstYQfS5XPM4lDR8jrg6uH/GO0UYkVU1x7OA41w6bR+445o0hm9U3jYx0VGl9jNhY%0AvlaSla+2w3Pmzz/r+0xLnVyq3w0e0//nADcNKrkUV0qJI4O8GBGW73vA0yuZBgdZvx988AE//sWf%0ABG3Z7Ru0Nby4eo2yRgSnypIQHTEWeO9wLrDd3rzLpTkc7xqW/jLwbwD/ErBTSmXM5CbG2MQYb5RS%0AfwX4i0qpVwj4+xeAvwf8b+mxfwP4FeC/U0r9h8BFesx/87YO0vc/AqiIIQFkQAwe5R0mgZlKKXov%0A7QSfPtDOd1gt08FGydi+TvdFL1iDDw4fRBLR946uO6F1AOVxiPK88h2EAkMcxIIAotIELAGHMgVW%0A9eguEL3HWAGfowfXeTw9ne9xwUEMqGKGbzsKa1iVS1zXcWj2iNuqwUUhlXk0utTopEEbYqA5jho1%0A0jWQdnpovGi6dp7oAypA35xwvZQAxinCvseZwMk37HY7fHCgPd54bFXycndFcSpY+J6qkjKx1pbW%0A7DkejxirpP1+EivWj7/3TGZbMKxWK467a07HI3N7QbPb07YthSlpm06yIWV59vELYSyfX1CXHhUF%0ASP3oN7/HrKo4OzsbCF9939OnebA8fzWSJt0ouQB4F4QQaBRoab8GF3FeOoUARRqY9F5IhTpNLIeY%0AyXF2mKQWen1BRLHfH4cNaFrCxCgAcxuSTIWWjDrCqFSXCG8DthJlZCD2SWWxEDnMjNcpxGVx3FcV%0AXoeEuygCMlsVfEhl2ZEsWeG9p9fvsb0+EoOmrOfMlwvmZ2suLy85v9igNXzu/R+jKCzbrWa/3+ND%0Ay/X1NVfXr97t0kzHuwaYP52+/607t/8p4K+mn/8Mgq79NUai3Z+Mib0ThQvzx4H/GvjbTIh273gu%0At1q+MO5Kd4++7/ExiDiQ1iirBr9qpUQtLJdIvUtzSMgu+frqJefnG87Wc2ZVybwqqazou5CwC6UU%0ARZpb8l52j6ikpR2iKL2VVuOVRSHdhaDcrVpe1OKg92IBq1G44yntQpMdzWiq2UwyFyU097Zth7oe%0ARtvWwYzeSwmVnNilhd22BM8AuOahz5tXVwJURyiMZblYUBa1KMH1juZwpDu1HPc7LvS5TFg3DcZK%0A1vfw4eUtEuNms2GxWHCzfTWUpbud6IrkNvThcBg+t2z9mtmmdV3z+c99jqYRz6O6HH2hMpCcP+Oc%0ACU75JDFhEiGqydoYCW63s4Ex65z+H0b8I7d0x7a0aAcfj8ehDJnP58PzT4+7GOAUY5uWWrdGV+5k%0AMnePfLtkKFPrlMTDcm5gWH/06gW/+Hf/Lw7HE+VqzXK1QZcz7t2/5Otf//08vHzAy1ctu91LfvM3%0An3J1dcXLFy/Ybrd881d+7VOuwu9/vCsP5tMLw/ExJ4Qw96mkuRjjh8C/8C5/+wc57naKprdNU8xp%0AT1/+rwZbCWNHOrfWirqw1KVluVxwfr7hweW9wfpBOjcBomjFDqlqyqyCUmgVpbMCaSw/QupcKKUG%0Amw9IJmSpCxOc4CB9246dDwUKJfoyyegrl1z5a7ow823WJHOwENPEcWC9XnM8nASsVeC8lF91UUOV%0A1AIBG8CkUgwU0Tuc83QhsN9n8qHHJBO4fBHlEiMT/XJGEUIYMKTM7p3u4rmcLCYdDhEOF1W7fAiA%0AqvE+JgYvaC3Yh7z+XFZEnAv4cNv6JONQb1s3U37UXfB1itcppW5hNPm1Z3rBdO3l87kbNKZB7tOO%0AaXC5+3PUcfhsSKs4Tu5XQ6u6l7KHHudPbF+2bHc7qsUZN9sDr17uWK3WlEZK3O8+/UgcHdNr67rf%0AhbYldz+wu6BXJruh9SRo3J7v0EpjlB7EfZZJHuH8YsNqPuO99x9xfrbmyeNLzs423L8vmhkGRwg9%0AsU87khhP470jhkhIrochBELs6LsTvutpT6eh7Uz0oALGSqBRylBXJfvtjlPTcEo2rCq/rtzKTENq%0AldLD/M6tCzQdA/fHibZsXVfiPWQ8Hzx5j4+fPpeMIXgOR8EzlAtycaeMxBbCIt4dE/6TlOH2h4ad%0A27FarSQAFOd4H/C9w3U98/Q+VmXJbrdDRaiKMgHgga7vxVq3LJnXM+bzOdfX12gUTXPCZTVApfCz%0AGQ/uX7Lf7tjv9/SteP683l2/ceHnC/zue+L81GspDnjFwNBVox/1tP38BnPXTIXg1ZDNZLa0YEQj%0AW3f0yRoB/un6vQUu69szSPlvDfNlkyHHITjZ7OekE54kXcT8fLoQ3Eg6Sztmc41H0x1ORBP5+JNr%0AXID9DkFPc3QSbTPKqhBW+Vv0836Q44c6wEyP22j+7awlILs/ahwgvFUiTb60gbK0nK2WLFdzNuul%0AyBHMSjEJjz2+D1ijUUnBTASnFCFPEAePT8Et+kAfG7qTeP24vkv6r6NJPH4kdbXticNRLqJIIEQ/%0AGpjplAqlEsy5jtPpiPd96kwwLGS5GOQ1lXWFT6UWSDnx8uVLcpu+D+NQYuw7DKOcQJ6dqosep0R4%0AXGuN0Q0uiL8OMDg/7nYygBiRC6/rOq6vrweORc4i8gU7nS4esILEySitJXrxY+rbTgDjENlut5PP%0A+s0MZKq7M91Mxk0oJCzj7ezqDOxO77ublUzXznT0ZBqQbg++jkS+21jNeN631uHkMd/vNgxDgFEq%0Ak/UYgk3uiOYyODtPLpYl89WK1cUCF6E59fSdpzlIe/5qG0SBU/c4oQx9puOHPsDcbTXmXSHfl9Ny%0AU9ixXZ2wi75vxTPIjPMg6/Wc1WrFB597zL2LM9578pDNasZ6NaO0hr5vxLjLaXSMeNfStp7u1ErX%0AKkQxtk9DZ6KmdqBNroWd6+lal/CCfDGNi2+3PXA8HgnOyyQr0DoRGvdEQvQUGHzXsd8fBt/qGOOg%0A2Jfbv/nImYBGQVGgZ/K3ZrOZZFJBs1qtpHwpyls4gMtB08yH3bn3nqoybL20zJumYbFYYK0dJqUX%0AS1FJu7q64ubmhuNxO+zAWcSrrmtevHjB4XDgyZMnPHv2jN1uh04SGH3b4rqeK/Oasiz5/Od+nC98%0A4Qv8w29/m1evXrHcyBhC27aJnChFqNaGw2Er75n37Pd7inKUhIAwlEhVOaoP5kAXgh+1lCf35YCY%0AOz7TUmrabs6T+tPHFcU4UZ6zzLwB5iPfn+eScvaTnzs/b55OV0pBkZnrDPNrrp94hifAdz6fY/a9%0AlNfa89Wf+oCf+MnPs3m0oPcdgR6t1aCNvNtXdG3LyxfXdF3H0w+f862//e6zyD/UAeZttWvOYD7t%0A8XlBCJHKM69qCmMHNmdVl8yqUsS1rUbj0Bo0knVoPIGAd/0wrxSdx/cnohdR7BBCGhaLeNfRdQ19%0A1wE6bS0erSKubwkuYq3wXpqmIeIRP2Mvs0k+EIKj9wJMG2tQhTAKneuJyYJDXpshs1Nzi376urXS%0AKGvBpyB8BxcAhsWbd2XfT7KbKOxQmVtSFNGAldJARxlFOHUdbdPw8PI+hTZcX19jlRaWaUgdj1T2%0ABeeY1+K6YNLtmQCnlBqm1wEIkaurK9bLJZvNJgH3I5t5CvDn6ebj8TiQ5ZxvhvtV2mBgtEuJjCVM%0AhjnehulNca5bpfaE4TstdaabXv6aagZlJu+0fLoL6N59vin4PH3sNGuXbFYA37xZzOsFs9mMk6so%0AyoA2LQGH50jHEas1duGoyp715X18V3N+KYO39+5XfOtvf/ut19X3O37IA8zt0ujO53Ir7Z0u0VYx%0AJQAAIABJREFUFK1kd3Cpm4INPLi4EALdoqCeWbSJEB3EHvyJ4+GIVhEVhSUZk5tAl7x3uu6EiqJd%0Akj2YI7L497sr0Z/Vwg7ue0/nHd2pQduC6IRCf7Pd4bp+4Kjkar2oyoTBCDmvOZ1oks1qBkhzGg+T%0AWayh7JMxgqooCc6jglDJnfNvXkRGYwuRb1BKUbkaF4TJ6bzH9COorJt+2KHz35vNhBT44MEDTqcT%0An3zyCWdnZ7fme3LZ0LYtjx8/5unTpyg1cpFUiBTGDuMFGsE6vvvhh1y9esWXft9PMqtqTq6H6Dge%0ArodMrixLZnXN5f2HvH79mv1+z257QNtx/EJrcSyIMSLd6Uhw/ZDtVlUxSEBMMa1pBjMdM5lmfHcx%0AlEHE6ngYfieXi3IuE/3fvD4ngcYYkVaYCpPloCVSICGdo8IYKUGtKfE+0jQnKXsSZ6c57XD+CJww%0AxQlVHejiiZPf0vgbCgxlqdEmskvcqmJjKG3F4nycu3qX44c8wLzZwrsb/WMc5zOmj5kCgJnHsFgs%0AMPRoLTjMbF6xXM2AgHcdEYcwUESgO4RA9D3BOVQU8logYyap/eh68aWOnugiPkqtO0zbKgE1Tyeh%0A0QuomxZzxiuIuCBqesRA07V0nXB5tNZDB2M68vD/svdusdZtW17Xr/U+LnOu+3fb+1zqcMoDdark%0AoqUV5RIiJgrBB2LQmBALY4gxhkTCg4lKSCQ+GJ4kBvQFXiBGE3yTiwoxkRCkBAErpooKl1iUdaza%0A++zLd1mXOecYo/fmQ+utjz7nt/Y559uYgl3H/uXLWnOuMccclz5ab+3f/u3fKg+kxOl+LZzBm5OT%0AzI7DSxUhFpp/FhCNxAikSBeAOOJ6ITNdbaHr3+v1Us5P8TRy603VGqmG7XyKzbjxdO/SdZW99el2%0Au2W/3xNj5Pzc6qfu7u5qGYVf22EYzDNsDW7AgPiy0j92fI+F3u17rRCZb9Mal6P5x+oZtgbCF4Xq%0AYTapa/95tDCe7Nuvm21vSQIzSpazjDGSwnrcXS+MY8eiA8Omox8EFeuMYcLuysPBkgZzsnCoyz1J%0AO3rZ8nnGLysD07qO7d/9dx/+MMZoRXlDEyI9fX7G06dPePHiGedng+n1SkZ0RiQTWEjzRCr6uGk5%0AoDnTARI9pi5xPkrQzNDHQoZTptm0Zw/Twn5KsNshoVTozgtdF1jmmcN04OH2rh5vFji7uYJ04E3p%0AT3MmA0shZXV9x8ODKdwdSufHunrOD5AtO6Qpk6aFMXZVs8RwgxLv94OtlEMkLwsaTSlOOqEoBBu2%0AlCaeDVe1MLPrLWO02ZiB+fDDD9jv9zx58gRVZewNHzJqv5EX53k2ofFkGjR5SfSx424yHZixHMvD%0A3d3acRDTjbm4uGBBq1E9Pz83b/Hujs1mw+3trRVvnp/zAz/wA3zy8hdq50JVYx2LCHTHei4tLlJb%0AzTYM27ZjhD/cpwWKbQbKywJavOZ07vo5tKxxB2VdFKpmBBtw2DKUK0WhljQkMEaJVAmMZVl4/0z4%0AEfk6+/kJ2/cCfS8wbslRybF4XCosspB7SwLkNLGbEyl+HxqY03GaMTgd7SSwUnu7KbokKEWL77//%0APs+ePeXpkyemjpYOqJgouIrhJ9bAS1BdK69FVk6N6cEZhiBFudE4LseelqeYr64NQL172NVJ4lmQ%0AEAK5wEqqyjIvVVtliObSt5O+XX39/zRPBQMpRLuckc4YqUDt1RNCsPL/5hjNLYfDMlnKWNXS86qV%0A5GcPjz2kl5eXFXNwUpq7+i3O4A/I3d0dwzA0+5HqHfjxtx7a0PVVq/jZ++/xySef8Pr1a548ecLl%0A5WU1Yr6NZ3/ee+89lmXh/v6+guoeErX1ao/hLi2u0lIdWoNy6uE8lqFq731rlPwY/Zo5h8gNTgvq%0Atl6MebulBcqydovQwvY9zTidn4+8yM9YdEu8yXRnyj7cEnNPDBZaxc480i4Y+VGXVITSvg/bloRg%0A5Kq6MohlSnRKx6xe2YCaLtGyTMRFoTfuysWm42wz8IO/4n2ePn3K17/8hKdPbzjrFNTkG6IoESth%0Azwn6JXLoMmisK7qT6CTadg5CLprphkhYFF1gKJXPEeHNfEDnhBx2QGCrmUO3ZZkMG+jHkiE5zFxc%0AXJAeEof9gUs5IxBY0sparYWDTaVuu2pm4FD6Y0sn3DKjvRvcjEgysehNIHeJJUZmtdS2VUWXSDMJ%0AnZRe2TGxuTYhpXGzoRt7ksAyz2zPzzm/vCwdGhND6b/d92MFX4dg4dfzJ8+4Prtgv73nzZs3bDeW%0AGv/05cf0fc+T5094+fIl8zSDWo/qeffAw88f6ur9ySefHEmh3t/fsywLDw8P3N/f88nLhR/+4R9m%0AWRZevnzJRx9+wP4wsxl7lpTowsAw2MPtD2r7QLe4iNckuYE69VxagXDfzyGURYiEFoNphgP6Qtrs%0Az88ZNxuG0pEz9L31ES9hWNd15he7wQqByIZeOrpB2ZyZ0dntdvW7U0okEZiUSYXri2skXMCwI+WZ%0Asz6Sz8/J3UxSZckLGSWrSb6mbiYPA7uH72MezGrR315J/EEzgE2IceTsbKCLgS4IZ2cbzrdbbm5u%0AeP7kaW1GZVwJF7GyWqOsibxkS1OX0gCJPaFgEoadJLIeTzj3elI6ll40sSvnbawp1L6PQGa3W9m5%0AhkPkI/0QumM2aBuzH4HbckJkEEGxMgZ/20oVjovtWm/j9IGJMR71UHYA070vsAfCiw9j0Z+Bt2UH%0APKPj+0hh1cJxsNUEqg61dAIsE+jH6E3dRYRvfvOb9H3Pz/zMz1QC3/3unlevXnF+fs719TVvXr00%0Apb9xQwhOYotH590e62PA7Wn2qL1Gb32+0f9pw6qcM5eXl9VTaZsDnmKLj4X7x9hSONqmDZ1ijDAZ%0AAxuJdU508QyNC9IrWdS8dKxuL2vjSU974FTm6buPL7SBOXU7uy6+JdAsIoxnvaV/xZrav//+c/ou%0AEAM8v7ni+uyC958/4+bmmouLM/q+Q+cJgokhWdYorQWNoQNsRbK5GKzlZshEemBmLmKNqvBwv+Nw%0AcG7CSjO/ublBVfjo2x/XhyWFjnk5sD/sORx2JY63sOD16zcmcVni+n5jGIVJQSrzZDoyUEK1cn28%0AyLON+33CViAzmqTBnFIBlFdjg658ouQGpu+ZF+fvwJJmDpM96HleymcL0XCeIR+XM7SGvwWKh2Hg%0Abv+mhg0pJX7u536O58+fW7hXrpOqSWD6ir0sSy3h+Omf/mmurq740R/9UX7yJ3+SFy9e8LAP/N2/%0A+/eLzOlTvv71H+SrX1349gcflLkTyvcpw9C/5cG4V9JyXNpr2ALrrRfpoWe3WR81N8gOgF9fX9dy%0AijaUfCwMOx2P4Tp+PX3BcQxGBWQKZJ3JMwgdKe0MIO4zfWcAvwQluRHtQTtls9kBP/fOz+gX2sD4%0A8It86rLWeFUTEuyhG4aOi/MtIqZcdn1xzrOnT3j+4imXl5fEWCqPnXMSxDgaMZJyB9l4ILMrr7vn%0AIEURjUTQjhASOawPkE2OQAhFPa+zzonzPLHbPzBPpZapH5gP9pB2ATJWl2NNvCZj5EbXYEl1hW9j%0A+dOV9BS89GvWrro1u5Q97blu59f1dIJ7pseNhfc7IjXAZwmRyMm8JrRqpKSUiSFay5W0kLSk8rPV%0ACnUlBT/t9ky7fW2lQfEu+86kMtI8Gzu68GgCcPfmDWebDV//2td49WpNY+ecefnyNWebDVdXV1xd%0AXVmx6LSv+IcBpG6IHfNwtmwsi0TALodhWUfhaG4Md7COD3FYjY0bmFOh71Mv5bNwndNMUrtwtIal%0A3T4E89gnDZCkLEqJtJ/RkAkxFynUYiRjblLoAZmHd3gi1/HLwsCAXUQnXAGVNxBjpL+0YrmkifPz%0ALV1voCtZubw658tffsGXv/we4zCAGl9BYyB2Akug6yIh22TPy2xGZFmAdVWeCrImCVSsBWmMQu5g%0AQEt4tKZol8Ue9t1ux8PDHarGogwF0Ou7kfPzLbvdgXkx4adXr14Vd7cUDw6lBiZzlAVp3XZVtYr/%0AEwMDHNXMpDkx55mki0llylD/bmJX3vbU3GjLHHWMm57YGZV/WWbDuJDSbCwRSlihtbXIemyOFcAa%0ADpmXcqg/LZsy8PLlp5yfn5u3tMzlfhsHaRx7RAaWZeLNGxOcSinx6acfM44j3/jGD/LJ67PKtxnH%0AkYd7owY8e/KUnBNLqcQ+HA4VVD2dX/6zNQT+exv+war1Ugss9+moTUhrYFr1vMfCnNNjaH+v7Wea%0AY3P1vBbgDSEQ+xnZHch5zzztyLoUMmMi60ImQ/Hk9mXBtLAwME2fr1bgC21g1hvgN3dV7gLqDewL%0AO/P8bMvl5TkXZ2eECO8/f8bXvvIVnj19guaFnAN9V/CELpqGawz0MRrpTTK6lHL9+VBX7RACMXSl%0ABqcUpnWdqcLucrmJa41UThRynnE2rq6u2O/33N2V1ThntM9sNmeW4p4S+909aV5Alf3BHswuDIUw%0AuGacPLPjEzjnzK5sfzTZGkmFllDmkx/W4rqVayFHWEqMYcVXSvZG1Zq6eXo3+IPZRbIqS+keANbh%0A8uGwZ0oLaTqwaC64kBYPpXBglsU0dNUyYMtsspSohWCaTe/FwzKRwDD2TNPEbkm8efWa5y+ec3d3%0AdxKSRW5vb4+0XDz8Oe1dVEOdJmN36hm2wLqHSb7foRgXT0H7QtB6he55dOG4KVvracKKWbUV3KpN%0AL/Lm+QAq52hJOxDrnYUYtWK3OyAhMRQVAU3WK3Iu/dmXxeZoyv9ougr8YzXazJGqrtKSm8DYKUEi%0AQcwdvNiecXG+5fxiU5i7mSiJvi9kJZd0kEAu0pMgSAzEyKoL4mm98no+mOj2fDggYnKEy34ybVMN%0AZUXXuoKrJkwgyUoSsixcXllb2nlaSKVUoAVt64TWwDIlXh/e1HP3SeW9nUTEdHhlTbFmFbI2hC/v%0A56zKbl7qgwRvc4u8RmdtrRLLRJzM5U6zpcTBcBdd+0+5h+nZnoeHB6t7ub1lv7dq7u12yzwfjjwE%0A92z2+wfOz89RTez3O7puQFFCFEJhsWYtpQP7VOujXr95xeuH13zzh36EV68/5fXr12y3th8Rw0wi%0AQt8NnG3P2e127B6MCrAt2jvY3WeelqNr4qzcNqt0OBxYCpHS2690pa2wXz83Tk4ehLXEQdOKRzlH%0A5zE85jFKQvv3I6AfQA4QJyQuMGcSSj9uUE3MaS7ztfQHi/a5oTOi6d19lcR+p/HLysCcZlHWONj6%0A8G42oymvTRPjk2s2m5HNZmDTD4xdzzB0eDWyD1uVxIBPkcKXUDoZykMNIZj6WsozebEHL3OAomjf%0AjtZtPZ0YxscwwBGEZZlP4vnQbL9mIVreTOuy1++R4wkbC6Bb17rideRsrXPb72kxGL/Gvop3Ya0g%0AdvH05FiIH29a/35ad+Pgad/3NUPU9/2Ri++hn3tqbtw8rPDvae95e43rdc7Kfr/nxfP3ub6+5tu/%0A+EFTdGjlFH5t2vM9BXNXTZm1pk11LSHw72x7cfl5tMCtf76VlTgNcU+Ne2t0fcHw7z8dp4an/Y6U%0Alf00m0h6kdMMcUACSDQ9ozzvGzwukNP+Oz98nzF+WRmYdmK0N6gLUvksNzdX/Lpf8yP0fc/77z3n%0A6cVZkWHIthJiK5WPXIBJyfa7OKGuALA2AayvUVAlxFwuaiCpZVtYxpqiXpap4jD+oHmGa9yUXkpp%0AZpmz9WaSiKjSh8hmGJgOCwe1VXP/8FCzFj7xfSItIuQy6Q9pqjUtbZVwGy556LPoVMOB1rD58faL%0ArbLzciCPVNf84e5+Pa/GpV8mC/nudw/W/uXsjNBFBpTdYc/VlbWrXd68Zk4Lr2/fsH+4q9/bn58T%0AsJKM3W6HaCqSoEr2a6iCLpmgdn+GoSeEkZwTec5cbDekLvDRRx/x8ccf8/z5c77+9a/zwQcfWIZQ%0A1RaF4n103UBfOUIGchopscXQHC+a6kPuZRI5Z548eVJ1nLuuQzZvh6hex3V2dla7MHiI5PeyLak4%0ApQ20c701Im703xK+omdeJnY75dNPJvb7A0sGCVquGUhn+zwbLeNZQ0X9/5m8Rw9FGxKcnVsBXt/3%0AjJ3FwmfbkbMzU60fh44hBCug2z8crRpZc50I5FZGsdxMU+21G1mP4bjbn3SHI6/AJ83pSmsP+XLk%0AeXlV9Ho+j1PO29f+03GArOZhLWlGySxpzbK5Cx5zMTB5PjIwvqI6VgNNxmluOCgFsM0li+NjLrUt%0A+yK05XID/t7NzQ2Hw6Gyk1uJUA/7WuqB1x+FEMhp9ar8nrdZGR8t5rHf73n9+jXPnlzz9OlTXr/6%0A1OQ2ixEWsYJV927cMzn1EqqgeiH0tap87sF4P6m+72FYPQm/5h5WtQRBVa3Fsr6vx+a3e6+n7z0W%0AJvlroQONoANLjiy54/bOSI+H5ZUlL4pC3s1VV87Br8Nxv+rvdXzBDUwAVnfSswuxozToMgxE046h%0A6/jy8xu++t4zvvrkhq986csgmYgS1RjA5sJ3daICBC1SkEGhZGMUSHqoFUdZQSVA35t6Xs7EfEaa%0AJqb9njlElq7HKplmpixMSzLXnEjIgV7Me0kqBOnQoPRdKNjFoYhZTWSdCNEMVOi2NoGCCU2FECCl%0AqhN7OBzIZOY5kSN0omhYG40BBWOYV3Gm6HhNj0gsGWFPsXcsUQkhE4Iwd4da7uCAoxuj0+zGmzsz%0A3DdPt6ZwJ8LYd/Qx8OnHHzHv7g2Uj8KedbU/HA7VwLtB9PT4styTVY2lHTpUQZNUcFvVQtR5NrH1%0AsRtNfOuw5/Unn5oa33jG6/1r5kKENLxjTTubXORUcSnn3FiW7MDt7T0pJV68eGGgfMG+ttuRGAMS%0AMhIyN5fWBNXD+BgjZ9uzowrpOufCcVjtRtO9Jv/fxwg9heIAZAvnc7Z2KZoLVYBY5D06lEzoOkK8%0AZxgjz4YL5qw83Bt2OBVv+P/5xdek9FBD0f1h5vOML7SBOV1V/MZYGLAWj33zm7+K999/n/dePOfJ%0A9RVf/vKXLQwSD4YeYV6GtVbksZ/HxNjjzn+wtqGIMbI04JxvH6QjS37r/RYDkEc+5xWzp8Pfa70P%0A35d3ZfT2Ju0+HRep5LBuxuqKzKjgDePpCCGjnfM5sklfFgPjbnzt6930EfLvEzEjvpTCxc1mc9RG%0A1b2W08yKh2hg3pJnfY5X6GQGkYS12HqbL7JeQ6kV1hdFluLDDz8sImRzXWRczNuxCPdGYozs9/u6%0Aj77v2W63bDYbNpt1mzbz1M4vP986F04MTMtDaufUqeERscLE40zT43iMf97npF1bpe8iROHJE5OE%0AoBzf7d2neA/rlBK73QH4B2/t+7uNL7SBcaAT3C1d09ObjbV37Xtr/v7q1Ut++Js/xFe+9L59Mtrn%0ARXPFVURW6NMLAW0CdW89mHluyVFSj6frvC5qZWXODw/AzgS9u55xLBW6aWQfHxjuzBMZNXFYvKSg%0AVccPiOSjCaIKSVZN2Io3FYylJcxttyPLsvDmzZsjGn+7KnqKM0vbytS6AkIozpn12A6lhmiZ5qMw%0Axq+Ph2frpKfG8q9fvyYonF8ELi6u+PTTjxERri4uVvbu0gLMoKVrJsA07bm+esI4bHm1fNyAoj0h%0A2O+eEdPsC0VCNYKaYeuiYVn73Rs0S0l5Bw77uYRhD8YFasDy3c7auXiJh5933/elmdxA14WyqJV0%0Adlzvx8N0WEHkGFhQ07PpIlEgCibMJVLFr6pn7nMvHgtSWZuTFdcxg05TwU0x9kUSIo5FO9iem7u7%0AO7794T9gzmp1dTHSD5ZGv765JMaOm+sXZYEKwF9/5yf0C25gqCu6rTglhRgUCUo/RIah4xvf+AFu%0Abm64vr48Eme2Ij8Hda0CukXw4bgOpx0toPzYCNIRY9NqtBDvXOulQ1BJdN1QDYKqIJ11KMiABkFD%0ARGI0fVQJZEkWjoXjSehGxh/kFi9xt9zdcT9/BwqPcBu/hqUTZSxlEaoTQiR1q5dEXj+/hkOxEAq9%0Aotc9s754MHtiiMTQF3Ba6Xv3XtZ0/6lBb39376jVUrH7F8sisRp//+nXuM0C5Zz56KOPqgeyeis9%0A+/1UuEpTxVj2ewN0h8FxGRNSb6/5OK58F0RriNVvVl2c9v+pF97OtdN52Gr/VgwmHqvb+fX2OfrY%0A/v19IxbO7OeJu9sdqlJF3l/fvqHrulqbd5oN/V7Hu3Z2/APAvwb8CNbP6K8C/5Gq/p1mm78E/JaT%0Aj/5pVf1dzTZPgD+KtZ8F+DPA71PVV+9yPA7GdYUcd35+yWY7cHVlhuRrX/saV1cX/NA3f5D333+f%0AIIrmxRBzsTqhgBYv5m0RcB+PTngp7qRkVJRcNXhLmhclqZDUjEQ3Wm8hzQthmmz1nw90WRk22yr9%0AOHY9aXlAFbpuxDjHkf1+Iuc3pCVXT0VjXw2HG87WvfYM035vwtxtpqLFGI5p7tm+U5L1vu47QoAY%0A+nr+np53voYPVeP2tEbNDez2bCjH1HF2ZuHExx9/Ss5L9QgOhwP39/dHoK4bcl+Vh2Hgo48+MumF%0AhztQacDUeuZHnm3Oq0KdP9RuaFyg6itf+Qp931vV9rKC8r7d7e0ty7KUUoI1LX15eV49k2Ew4Pbs%0A7AwlM00zh8OOGCO7u+nIA3Ui5LlYdrIrlfiqBu5LCFaTKKBFYiMUrzOUjFfGBNFNIgS35iDGbQpd%0AJElA1K7hpLmEbKsHe39/z7RkUlIEk25VhWkJTEvm1ZuPORwOvHlz+y6PZh3v6sH8Fqy74/9ePvuf%0AAX9RRH61qt432/0J4D9pXu84Hv8t8APAby+v/zjwXwO/4x2PpzEIWsMSR7+327FWz2ZdGIeNuce7%0ABzZj6fVTDYY/cKbk1aYET5F6oCayPYRxNrE/rC0YpwUgJWRYIEiGsBB7W9W6YYRlQTNkUWLsyNn6%0A/XRxYIkQwgrwldYC9dzb+P2xFfD0by0GcBrXRy0eHit+ILKyd02pT4D0qIFpr1s7jvCnYFk2x39y%0AzlAeAisfsEmu6jK+Uid+CB37/YP17JnX9K0ZEGe4FkarOjvXgO6zs7N6fKvYlhmu+3vr631/vyOW%0AViAeVgKrJnEJmTabDdvtthp2LXVh1oTOPjvPh/rZ0Ah4u6FxPk87b+yaHwtYucFum8q11/cxDMZ+%0Ad4+81BXpyjRejeKG2MPZtifG3pIiqmT/noxd5+/eEu3R8a6N1357+1pEfg/wbeDHgL/c/OlBVT94%0AbB8i8k9ihuU3qOpfK+/9u8BPiMgPt97Qdxt+oc7OzohRODvfsN1uuLyyPjvvvf+Um5sbJGhxkRem%0AlOiHknbGui8iZsEr4s5xGfxp+wsbEdVsoU8Q48ukmWleYDYvSUKHEtAQyUGJdIQhkyUwhIimBZHI%0AMG5JeUeShX6I6G6HtY9WkmbmtJBVOEwzsetJBUsgdBUHcPq7r/itQfSHo/VU2orfdoKGYMCuTcyI%0AF/55PG/vZdJiPBTHGHxyu5ZKztpcR6sodxGlaZrMkBROy9nZBfdvXpOzMh2WQmc/PjZPcftDfn9/%0Az+XlNQ8PDywLdF1kmpZaYa0qJeUK02QeSdttoQW2DXfZs9lsuL6+5uXLT5inVNjUqTCMtfYiFxHe%0Ae/El08rtjnsw3T/cgSjD0NU5l9IMi1hYG4vhVMjRvsOa1Vs9l4iQezvvuaERdDEgKJqTZc4oNaOL%0AaQsFCaScLHHh4XEy/WktpQf7Zaqh6OXlJZoD0wF2h4VlNqP7sNsjEnnzsK/hoaqi8R9NseN1+fnp%0Ayfs/LiK/G/gQ+B+B/1RV3cf6jVgv67/mG6vq/yYir4HfBLxlYERkBMbmrUv74KoCFgKEYBWiAH0f%0AOT8/4+ysoONkUgIhoyFUD8S8AnfpEyJt90dbBSQ06Lx7TDgSb8JT1rUqNOHB2uZCWbNDkcbDWIqQ%0A0LghLIng+iZ6gpOk1TuoK2Do0SBHLjesIZJnkWxCHdeoNNf1LY8jalsiUP7WYC2mkxPI+W1ZDP9c%0AG1q0HlKMJnidl4VlmRn7gcPBFO0+etjj7XolHFcBG5Yj5GxN09y76bqBIAvzUliphaCWEuX6l88l%0AN5Kr4RMBLz41bGhimmYuL68IIfDw8FDbnrTnc17EoJxAl3UtGDWmQl9wIPAukzlnWJIZl8LuFsXU%0ABckQtPCTysKgq85vCiYAdkp+9GsjpVXLcaZR6jn6fnyh2S2rcuAwDJyfXSBx4v5uZpmtT3jOmdvd%0A7givegyH/F7G5zYwYt/4R4C/oqo/1fzpvwF+FvgA+LXAHwb+aeC3lr9/CfN6Tse3y98eG38A+EOn%0Ab3rthv0MXF5e0PeRZ8+e8OLFc549f1LYq06rX4pCfQECJeOl/+tDuAoqPRZ+1Ac1BPMagyCIVVsD%0A85I5TLu6Os6zTf4YbDUJsSOqklXYPdwVicoAEtEQud8dmNJi3fmysjvMHJbZFPNiX743QgxFfmJN%0Ai7a0dj/eFcw+NgD+uiV45Zyr4NCKY5iRNcPpoaH9TpaiCXwMhBuetFRDHGMkdsZHORx2JqkQAqLm%0AyYQQ+PTTT+tnQ8xH1/44e6ZrWQQDcGCa9mheSWI5u4FdRbRJayjiw/fj12u32/Hhhx/y5MkNr169%0AYSnYhIV0pmEsEjk/vyBnePXqDVfXA9uzTQ15NpuhfMdJAeS8gFpCIRrxm5CVZTogKR/du8Rq1D4r%0AFPLvG8aRcCQU1t5/L1Owe7ntI0E6hiGxPyQ0W62VSs8y7clFxiGnAMG0mK2A1/ChzzP+YTyY/xL4%0Ap4Df3L6pqn+ieflTIvL3gL8hIv+sqv4t3+yR/T2exLfxhzFj5uMS+NYaRw5styPPnz9lsx346le/%0Aws3NDeM44t0N14mVUQ2ejC5hUYtP1POwrU/o2PUn3sUv4A9wXWXy6n7byk8hQIEGA4RFBOkiMq9Y%0AjTdodxAVXVmzqy7JGpO3XIvTuPx0Yn6nVeiz349WpPkZw4+73bcf22PbGkEt04V1Vd1KTKfDAAAg%0AAElEQVRutyzzcVOzU4r76Xn4+8ucy3/zTM1zaDwyXdUAJa56N74v5+u0QLkzjr32yY2bs21Pca9+%0A6JpFrhXlLnVSBag1qF7oxCRVg2KaN+W15GIQQ0BLKJPLsbU1VyJCiBERkBys0vyoLW2ok9hvqxTD%0A5l5M18HFhRmYzeYBlUROkRh7Lh8se3Z3WxoFFvrCIw7w9zQ+l4ERkT+GZYD+BVX91nfZ/G9h8cMP%0Ald8/AN5/ZLsXWEj11lDVA1DLOX0y9/1QMyPeZP38/JynT59yeXVeigZPiGqsbFzxlF7T1lNPwKwW%0ArG2NTG5WF9+PC1+furIihqeYsfGVwDJBKWuz+m2g6OCmZFoqK+FvBTtbA3PsEr8tnbkew9sG5rGw%0AaQWR3Zvz47X+yu0S0OI8LV4FHHkehgstlWuj6oZIuby8qJmjw+HAZrMhN+URbRjmrv0Kelr7FzNI%0Anj1LlRyoXVizUJKPjJ/vx70ix3jmeeb29rYaGMeYYM28uDSGketWfZcQWpDfMcISuop5nP5f7MKV%0ABSkXTksJi0r1fD7xYHDvJQRiCfOXZSl6ycdgewv4tmn7ECLejM3S3gYCbzYburhhfgo5KeFqU7Eu%0AM8wKfLdH/e3xrmlqAf4Y8DuBf1FVf/Z7+NivwaiVv1he/wRwLSL/vKr+9bLfX4/hOX/1XY7nkN4Q%0Alpm7h5k5veHsXLm52bAZIOjCEKHrA9NcfPu8xuKWCDFvgtY70Ebztng45GMpBBFhoMnCiCEyMcDY%0ARXQzQloqB0ICpGVhyZlO1/5DqkCMbM8u6eLIZlw45Im43TJ0A3ev35DJdEPP/f09iGE7/SBISKgI%0AGSGphV8GSk5kEoiveAYq55KhkgLAZpTYRfKilZsDGGCdbUKFwmhVFavDgprtEfUCQBv2cQsnYoxV%0APMnCkMy8lOrcgu3kbMWc3/jGN/jZv/9/EcPAMu9gjMy5hDYSCAQDxYeBw5LoEKYkbKQ3nZyHA3mx%0AmjEzCAPzPKEq7HWuGN2QIx2mIbMsCxKgK1IE8zKzHBYWrB7p2x++5NmzZ8QwQMnATNOeJ0+u2e1v%0AmeY7vvLV54gI/XCGipWKWLnBQogl1UwJi0MgMUOwzp8hmscyTQW/KdcwFPLmYLePWO5hbLlNQYgS%0AEZWSvp7IYbHyEu9OGQt3ycPdYns7MjktQKCLiWGAOGZ03vPq9haVwHjW03UDX7r+J6rHlDPc3d3z%0AV/7ST77L41m+893GfwX8m8C/CtyKiGMmr1V1JyK/Evhx4H8APgZ+NfCfA/8H8L8CqOrPiMj/BPwJ%0AEfn3yuf/OPDn3iWDBLAUIlSM55yfn3NxcVGR/hAsppYD9INVgn4vMNVjq33r8ldDk9csVjmvo21b%0A7KblVMzzXCUMWr6I78MzQrDUfbdaL6dex+nxnh67r2R1u5NtzIPTz/hcOywcXD0AxcHM4+G4jZ/X%0AMR7h5yliynKtZ3J0TKd7bTwZHy1f5tTTUT0+Hy9n8LDIW/vG2GJSKy6Vs5H+ljRVT2e/39MPkc1m%0AW++p41Sn9+VoPhSGeAXE8xqaZwdSlaatzarb3A4RqS1mzACvXpU0JaZ1Pp0gDiG4Ds3KZ/KSh7u7%0AO6YlMR0ss3l5d1c9a5HI4fDufanh3Q3M7y0//9LJ+78H+JPABPxLwO8HLoCfB/48lkVqyzF/HCPa%0A/cXy+s8A//47Hgs3l1dcX19xfXNe3FPjHux2OysbEEWyEENJM8ua3rOXUjIWUrM7Gj/75gK10G1/%0AmI8eCp/sblR8BT8cDiBSAcU0L3hrWJY1xbmGfT0X2zPmLnH3+g3T3iqNPWWYc8aE9lYQug2VTv+r%0AqsX7Odf0pYjUVhgBscI4Ld6NWhvSnHOloatSsBE1mUVWuYfTa9XiQT6Jc84QYnmgbL9BAk+ePGV/%0AmNnPZky7cUOWglaIZ7GMZ2Tpb8g5Fb5LYFcyHVkzKa/3wCt/jVXsBkyLTOnaVVKCZYWogmJeyyal%0A0vuK/a2xe8/PN9zf3/OVmy/x/PmzauiWNJGylTRAKTER42WFYIugZKHDNGlUIUkglL5Z82QSoyJW%0AcCsixNK2RWIxJtE7NkYDX+t9pGQ4qffKjuFxAzMdDubJqlTD8vr1a25vrV3MtCT2uwmRyLc++ODI%0AY9emK8K7jHflwXxHJ0BVf563WbyPbfcp8Lvf5bsfG3biiadPn/L05ppf+at+kJvrS54+vUE10Zf4%0Ad1ochMUEvKm2BiiAm6f0OF5pUS1uvT00i1gDtQWOHiCf3E4b9+OLMTKlhdMQC6jSkuu5KJ2EGht7%0AT+ZsswIoxX+P0LZPQd52GAzdvn7bW/Cmat5eQ/PbXlHFrDA+DO6CN4bWQU114qFaVTsSTdhCjKsR%0AYkccRnbTbBk0AiFaij4QLOOilqETFYeEynfYNoeK6ayejXOBPGsILut5/ADaNaUBctfSCpGV4dx6%0AR33fc3V1xTiOFbPBOygErMkeGcmlLATrq61ZCUFqatrK782D6dQ9S6FrPF4R60NuYdHx/V4NCKSl%0ApLAlVO/0s/BYS4oElMAwzAzDsWD8Kr1qOshmiEtN3vfk/789vtC1SE+f3vDixXNePHtK10c2w2g3%0APS9GStKinJ4yXSGOIeXRLVyLWNLVvgi34Uobkvhkq3wWldrYyzMRsFYs10kSgnUJyGvxZC4hUloM%0A+JRs2rL7/R7pCtJfyIGmEFdi65Jt8Cpsf5ja43sMlD41UuatrFyKdnTZqrwlJFCnjitD16FRWWSt%0Ag+nD6im1Ho0dT/FcUtHTHTZGdY8Ggo/9wJKU2zf39KOJNHUOaGvi1Biv+821Sn6a9mWb8kdRK29o%0AjKEfhwntrUr5vi8X+R6GbbluM7Ez726e50qsizHw9OlTzs7OjrR87PvVjGy2BvSQCU01vWpiLKzi%0AQECWXB/XWDyXIIHI8TWs3mDz2j0YB/4d43EPxo3V8YWxYZIaEcVA7WmauL6+JsaeeRYe9gc++fgl%0AOUNK3ns7FMzs86WRvtAG5s3r1/Sd8OL5DZfdOYdpR3eAaTS2qWpCc2YYz8qEbfgvSPFcCj5Q9qnw%0A1oMKx/VIIQRrY3LivYQQqvvdcjhaz8K9npTs2Dwmz2UF8SZuqlJDKhGpbrQdjBmI3BjDNiw59Yra%0A7R/DN3zb1rNxmr3jC9VDCY7DpLfStn6d2vEYZuRhneMhrVhTu913OtYa/lUDWbg+0ja0X43JPCcD%0AXsWvkUtpHu/X9YX8vjnGEUtltBmXlR3tHKDVyNrc8tchgGogeNmCyOoLuIAZxaP225tPhKTK5m5g%0A6vmjdB7SN+l5D4VPDYzVoUkVple1iur9fqrA/DiOLEsmh5NwS4/v6/c6vtAG5vr6kvfee4/nz57y%0A/PlzXjy9sRtewLsYRyDXjoVR7IZHistN6cvTxEtRumoE3CSllEgNr8W9ClWjj+ds3kfFZ0qHwcqk%0AZa1PWpbFMgQxMh0MQNQlkUtJvQtBiRiFfFkWDg87m/zuXheXNkuoqyxQRbVbvKgF9UTE8UbImVTC%0AgYCQC/M4L/bQiRa3O4hVb9tRVfV5O58VoG1JcHb8x0r3M6vKXwiBLgYT8d4a0Bt7p8y34Z6uvHqw%0A1Kx4+11rV3JkLFQJoS8kPH+I7Mg3m83KL/KzcSJZhrRkljSbTAO5Vi47/+Xp02vOz8+rR1I92kDp%0AndUTxImLMNTaIzNqcVnZ3PVYC8aiJQzpyvVxsNcNjTTecOjiUVcGJ8Bplmp8FvdU5biGLohRKXLD%0AgL+8vCSlN+x2b5jTWkg76SrFgQbmcl/fdXyhDczQD1xdXPL8+XOury9LCrAILEcKDybSxVJl4N5K%0AMS5BwroClYmYGw/Ax2Mejb9/utKehiaqiooe7ceXpNPMh7WWmCvHwVe81nOK0TR65ZHjaCfT8XFT%0APRnkWKLBqC1rdsOaKIEfZMVo4tom1kl/IrxlYFxl37+/uvMF1Oz7te1HVxI3sWyzkCFpjffb6+tZ%0AHRcGb72n9RyPvQ5X47PfO1QM1LfPdeS8INJkg9Q+EwcH+ldtoXEcGyJdmyF0z0ULo9bCihCsr5YZ%0AmECUElo31989RjcghNBkktbReo9HAD7rvJAQG7DecZPVWNs+SohPqMRC96YPhwOHeWFZDERvw2xE%0AH8X9vpfxhTYwP/j1r/OVr36Jp9c39IOJIMUAsRP6EK1ATMT4HyLEmv6zyQR5bU8SysM+r/Uj9SI7%0AOFdXgcCc50dTx16cNs8r7oKcpFkbwNa9o7ykAiza62XOaAm1em+qVoxLSxaDFbQ8JdjVVPhyjMtQ%0AQhNTEy6HmJWspSBTpPJoQlwNjBuSNSTK5LyuhqrKZuiOjs29qFxS3HX1XRa6TV+Nu6oy7ZUchMTc%0AHG/JlkhgHK1v1XZjtVD9EGvbXPdk/LudkKiqxKJDe6QFo949IR1ta0bRz9E8mIuLi9q+xA2MX4ve%0A23x0kRjdoNg8DKwi8qErpQC+EDRGOcTjXlV+n/y1GyAz1M1cKpyuGL3/1HcGYh28RkwAPsaRb3yj%0A5/XrW5Yl8PL1G7794cekNNfWMa5X9Pkg3i+4gXn2/AnX19dstsboRecaAlWvQnKdeEhJH4oc4xGi%0AzeR6vIG4T8D2ofaQ4C3Mg2PMRir/wFfKE4+mGe4F7HdTfSBdhCnP6dEV7rF9td937LGU1ymTyjG3%0A08cxlhUrOZZ4XMfbGjlvG6C142SWkq0r2yeUKMWz9KJDzYgqhwYQ94f6VFAr51xDw1yspJduGCbW%0A9gOCQDw6zkoYrB7MsbE2L+mRlH8I9X0LgcwrCiV8C0GsgPGR+1N/92ycATRHCYH22tUykMZzafel%0A5V/O2bJ2fg7uAZ58t0XGWsXpvR+3iMlPXGZlv5tISVnu54o32S36PgyRnj19VlBww1H6fkBE6Ypr%0AasW1QgzxaHJbGGSN4v3SO79kKfFwS+JyxF2byQA2oee5XW3XJumtkFM6MVi+YrdGy1eww8EyUw+3%0AJpJ9fn7OYVfamub9WyCq77d1hU8NS125VckiR0azk0BuyFvOr/GHOsaI0varLkVSlNYtJQXr9mdZ%0ApiNDYO8Ll5ttpeIvy4IMfQV6U2ltohuTqdzp25IZMVqjtsvLc+Z5Zl72xFgaxARt5DGlgu2VwgqI%0AHqv+k73sQNCatVqNqNexuZfhGT0rLo01FAuyYPT7FX/xBzgED1+UrG58gBiIEujHgfkwQTDqf/Aw%0AVNaaI8NdViF658bY9bHsp+FIWjEYx8wyJwYpWKkAEq2GazHi58PDgwlPzUudL20BbQgdff99CPJq%0AzMTeVO5jCASSpehiREVNsxbQeXe8MuB8gSYU8hYYzgcUu4HTPBmVPM1H2SJ1/gFqcgEOruaEaKYL%0ARuFPaQGBVJrCd76olpAEN0CqDCFwKBM5kVgOztEQpkk5LBOSVzykK9ISOlu19Rg7pmlBrBk1kgT1%0AMMEnW7bWtZotvJCuw8lsUQIxJAw3VCCDWk2UtA9n+UQUm7SgaOno0JWQJqhhXDXNKx0hwxAifR9K%0AG5WJAAx9NPykHGufNnWiqyp5AZ0z57Lhqjvn1d0bNnlkio1oumRQ81Cdu+HGASCSVsQXx6IszECF%0AXELBHCNp7ggy0sWIqbxllJl+hNDtIFC0lzOEMwgQulhTQR2RmI3O32skEklxxtlIjtksaSL05vHM%0AZAhS+oIbmSg2EqcAUgyylwRQ4DwJoXjhlkHru5LpO9FJzhoLJSMTsl2TiyFwGCIhHQjzTM9Mzgfr%0AdhFixc7kl4Jo94/beP7iGVdXV/SCVdMWSUAHIJVcsYR2tABnDR/Ke2sW5xio9DYVVVUsHzeZ9+Hf%0A1UpXQgkx9OQ7y5ACNIhIbcA+z3MBoU3Ptu8z2+0WkrXEraX8GgjBVlGns6PHbn98S8zc2rAMfcem%0At0I958U4df4U52ld9Ao66lplawV8bnyMAhDLz4obNNf+aN/rG0fXrnpjwQsTrc2qufYDcz7Ua24P%0AkO1mTXs34e6yhjn+cLafbUNMTxAMY0/fH3cFKJ8q1/O4eZ0tOFYxHbvOFr0Q6EIkdBx5rF6hXT2h%0AgmN1XQddfxQW+rB7IjUNfRJd1+N3bWH3oP1vOoylkDSTk7AUJrl/7+3tfS3wXHZzvT4ty/ldxxfa%0AwHTBKlQ1JxAtaUwlYsWEiBCKlwDlISkhkvNCVHWl7rPiBN60nRCtmFCBVFLKpTK3penDcdhzNGll%0ANSJvzYpmnMbY7eSNMVqWoy0wzE1hYjCtEljBXcchHDOooVzZdx/W6m9/OruCueTGcLY4RDvhH0OD%0ATo1QPVbS8alLfsvAaBFhj8G/O9bz9AfBG7SJKGFasQZbyb2ljF1rv/aqQpLMSqgs3hnW38na83rJ%0AxrGwVyt+1Z7Sij85xqcrBiOWzaS8JhZPWoSU81pRXcDZvlRj1xR+v1m/Q1t8zQh1Vb5StRFDW8Pj%0Avh/Xujdd2eahy+Ty2ZykzuG+77m8vGRZMvcPu0LIW0N38/Y/H8z7hTYwjr2EAJ1EQsHNPLXmaboQ%0AnSFawpJsUpRANS6+Yrc9jx1MBAMrt9ttje/di/CJ6A91mwVwb8Y1YoU1c6Rl9XDCnZRJFKQjSEcX%0AjQ6VlqJMf7DWqeRsHQtCQHVBVMhJySTSvMM0XBZyShX8dMkFX1FFhLErMbYEz2dWoPLIiJwYjKOf%0ApQOBv27P+dQYafF27D2/vm70c63UtqxKbD5j++gLhuKfOaX3r6Cu1BBp7em0YjktrmMPjmeVzGAM%0Aw8Bmu6Ebe6QzY0EM1uFBKJ08V1mPWLC80Amxs4yfiBC7VasnxMj5uK2Gwj2GcTSQ2/EqPzYnhnom%0AUnOuiwI0HhsgVUwtmyy0lj7jAtKZAYvYtTukxJIKbygHrKNDj5xFvvGNb7DbHdienZtcxe3aCth4%0AMN+HnR2tLN7CFZswDYuyGPZMaWUqzny1/1omtSPxgcezLr4CtC6tA5WwupC+SrTAavvaw7C6/wZo%0ARbXiD7A+nJrMOO13h6onK1nI4vwaw06c+JUzhLAKK9VMh6fpYyOUFLzYkWr8uihY/Q6sPBgHtf01%0A9WcbHnqS1D0/OfnvBqYybjk2VjV0wR29VtMkIAHmqW1rcvo5xX2hatdOvKjT7zTDcgxexhirmLdl%0Ah/Qk3K2zDy+SdA/TlPsszR/7VeTb3h/q97ZKjK1RtgLMwFQyk8kXOi9MbcJvVSWpIoGjueqZR/+9%0ADeMPDw/1PvhnpmkiLVoqqh+qp+idHnw/jyUXvpfxhTYwooYv9F2sql2QrQReBS2aHLUpWFrxFs3G%0AGsVXuzLhhq5nVqp76SpruVjwPna1CHGaJivh7/uaaTo1LCJWVu+jNV7ed0dTZoid9c/p+1L1G0hp%0A5v7+gYcHaxw/z6lgP135/Iob+QR4KLU1XdfRl1g+9KGGRHX1Lg+osE5cVa0hYm3jUljP1RtZc59H%0AKf3WQ/DXfr4AxFZzx+ur2m1zqeMRXDvKrlUoAHpXCidN3c+A+YKXgTFOBJzflHMmlNqznDPEjpwb%0AZUOxh7P1YD3trKKoZLo+MgyR0BXcI1glslSecKDfWA+kTelY4CHnZrNp0t0RpNE67jo0rNk7b6wm%0AnZEBu84WsvFEztQXtZQzIURunj5jmvZr07wy7zyDmVM2UD+vhbixE1JSDnvb136/ZzosfOtbv8Cr%0AV284TKbmN+2ta2UXAoSeNH8fGhh3tddYdV19RTEmZ1DkBBcxvEFLJsfdadZ9sbqhnkptV9gWqKzd%0ACE/qknwiG55h20pulNma47GsUdmHrt895xbLcSv1dguVnO2/PeTxaFUVKQ+DrkbADQscr+hBqazj%0Aihuxvj4d3wFOeguDWf+g9VhClRowz9PfV129rxWobMWt9Oh+lHfBjUxat6tGT47vm//9lCpQyXdY%0Amrs1lI7xWAgmBb8Y8T7eZpStWrk2NSqV4niDwBAIXV9SzvGIgu8wXSrtWDoCQdfatbV1inFV9tOC%0ANqp3p+Fp63nlbJnWNK/yICKWjhdWLK4SI/NJk7rvx1qkAKW2xkC7NM0gmVyqW6uil68QzUocKfG1%0AP+S+si1mCCIWly9LKviAVtedph+QeRZzvSFtiFQntLf8bA1MXlfvZVnIs/XU0eBFddYjyMIxN1wG%0AEtdJMK8d+lSVrjdJhLEfGMexZFMSidKYPq5yFev1MABbaizzOIbyqMFoqrNDkGOcoGSPQrnmCyvY%0ALYawF06GhX02vP7LMkax1BWpziUkKgZDMjmnYpjWY6aIYgXBtG3VQuGcZjSU7/VsWk6omsJcSkWy%0AUtU6gm56+nEk9gFiIKNIF+mGjm7sWZaJvhQGnp9drDKpAoqBt9J1ZthjJANzCbM7EYa+BxGyCHFs%0Am2XYtVym1cvqQ2AYzbB4L2xfbA7TwnYzInGtrk/zTD+a3GdS5ySVexqUab4DDGual0zOe/OWxtG6%0AW+6MazX0kUXsu0SEtHwfGhjwtGubZnRUZc1a1NWaRoAprO58u7KtGrJNe84mFPBxhLDX7+bodX2/%0AHEBoYt8WbLTvKcanNBhzI+XGxfs2ac5W7ZozuvjEApvagbZw09uo1nR3rSGSWr3rWjjVoDSn2RqZ%0A0/Nvz/U0w/RZWae3PkuCenmaJm7+2aC1Ctk9BjciAJJ8e22MzEqOU11rpRzMbb/fh2rB4UKohrkf%0AYiFNrrheC7I6ThHCYCFr8QpVAjEMSBhsYSth6ditnQBcjMz31XpJqspCqvos7Tbe5M2Hpe6Pa7Lc%0A4wZqXVhlP5cWKyEAGo8Yxy0W5Pd01ZcWpun7kMnrT0MuKHuIFItrf1IslqZgFYu71o1HUwvPyko7%0AN96Jx7Ptg+QP/lyAVWd4trwD9yqqdEPvLT8hzUv1YFzUeVkWtNQiaQgVy1kWq9K2trFFAX+xJmEp%0AJYJ6M6xcQUNlDY3Azqlzlm48NjCqWtkNXninRwZmxUkfC4diQ79vJ6fzfaTst71XbvSEdd8mWt0V%0AmoGQdL3mymrg1y6K1ghOuhPjpQ6WajXafg+cs+IjqXuaJhexGfq6sEzznm0egbVwEmi0fDs2mzOG%0AYaSLgzHFS61RHHpi1yGhKxX4gS6uzekygTkpQV1bqKMvFdse0pxvzo7mnp9za5RyNg/39tXHlWUe%0AGzA4hMDFxcVR+A5weXkJBOYpMy+Z62srD+i6V4QQKg8rsRqZdgF91/EFNzDr0MI4La8KzmDyhd4E%0ArcbbfrEa/ot7N/v9VFeMpQhC+YroNzulRNL1prXeyuqRrNKMGtaHtyLyycDoCgi7gQpt87bjamvL%0AODWSEbiWrZ1OW7fi49SD+KzXjUrJo9s9Nh7bVzsRv5P34gZGRAq9IFRtE82ry9/uxzEbymd7jld0%0ANzCqXh+21pc5/6M1vLD21pLOFoqHhwfCKIVwFhFxmQnDgfyhW9uUmCCTlQsEutgXItyaQxMJ1Ti2%0AWE+M8ahzQdsbSURKQeIq++keiddgqSrx5ob7+/sjBT5X6RtHa2TvomgSlH7ogUBa5loKsZJT12Nb%0A0lrq0no37zq+0AYm5Iw4tT8IKRVXWhXVkr4GTAPDaO9HWY64GoelTOY4NilmycTRbrzzY1SVTLYW%0AnimxzMaHySWjoTkTROmiFJ2RxLIXgihL8X6oot+JZZ7ZT1a5upt2cOgRIrosHPYzy5xBoym1Jcs0%0A7R8SMXZM+d7c77Gni4EYE0Ps6CIEyfTuPxRPJKB2zUQQTcUzWBrsJJOqVtF3x2A8pX20uhUekoai%0AvFcm5igJBx6rKmBRt+sLJb56CpyVhaDUe+1XzpFnBXPODOncji2YmJRnS+aSKVkWJS1C1IFdvrdw%0AczFcoe96hm5LUvNMdve3EIQnV5f0Igwh0EkwMD4lREZC6Nlszhk3PRJGUg4kBkI3EHoriUgIec6Q%0ABZGBsdsyjhuGVv1PigJdEoYw0DEQtSPqgCDEUDzerkNCoO8N3+lyZs6Jh6KaqF1H2A7EnJGSng4h%0AcDiY93wozd5yNyIyMi975skWpiWLZcTiwLjtefr0OWjk/s6yUg97m1v7/Z4pZWtL+znGF9rAVHff%0AXnDqxH2nFbUalpPmVt7A7jQ12HoRrUL9kafiq2WTTQJIea5MyJxzRf6dbbmmxDOa5xImOFAsdaX3%0A41n37cbCCxV7rPCwq71ypIlzTrV4LZxxhNflN4/TzKc/j66v1zfBseHWUtFOo5JX2n8MTTjghsb7%0ACvl3zCV88+4LuhTjdBIihGFANRlQLJaOXb0eC0+CGEYVk/XZNgPl11qZluNFp/UgwHgiIQTOu/Mj%0AOn97/JX1K1KLEUO/Gs+u62rJd4vdtQbX93t6nW1Bs7BzGAZiwYrmeWa337MZNgzJQsbaHC6YQY5d%0A4UMFS0J0vS3A5glbCD7PM9Nh4c2bN0UA/NakYPf3R/jO96UejLjCetYjEK9O/CZr1E5gj0vbuNbf%0Af/npx/W1P9CuVufbtIap/e9ubPtzVVFrDEzxhKZpNnRehZwyb97cgnZFJc8req3bYJqTyRvOk9HX%0AxVZJ74fUdQNj8QT6aECeMXWFLPM6sYNzXawxu6VWM51zZMKxQW4xgNPhdUsW+nmI6PU5LsZk++j6%0AoYo3+b3wB9RBSL+2wUPJYGTD3AfGTb/iOc5d0QLmYqtyypPV93lKWJQcS9iQrKPhMlvDtv1kLX2n%0AaT6aFx6aeIiMZMZxrNyizWZD14cjslw1IgClX3g3DtXw5JwZmnqm04SA3xvnzKRKGCxJhILF7g7F%0A0HYbYrdhe3ZFzhPjmbWIt5A+MZ6PqAqb8j3zZAtg1B19ZxXrL1/ecn+3Y7ud6bvMixcvGIcNOZuu%0A9EefaN2nZGWaf2nalvxjNeqk9OrS7+KxVI+n2c69DzcIbdzvhsMR/dYgnWaOfDzm4ZgO6vp3TrAV%0A25/YRFDjO+ScGc/OGRYrnZ+mGT76iJTm0nZljeO7rjcSHbF6OyKBvq5AxTvr7H2zIbnQxXL1gETW%0A7jpvGevHb0CtA/LfQ13x7L8Dt10xfFWYvbl/btzMWMCij3SmLKB9rWikKVTEQBQ95jwAACAASURB%0AVFxl1a4xA7eCu/adVlbi1wMMg2kpBo47OB7W9101HqdhY+u9tPNsnmdiAY3No3h7zrhxbT/nc6Eb%0AztZ5KuvfU7bMaFrcKJk8Zj0OjYRshEz7HvNYtISqeQKNVrM2jiM5wWG/sMTM2dmBZfa5tvbxfmyO%0Av8v4ZWFg2vDIXXQHVU+3bYEsoKrPuZfik6kFatuexT78IWnDpDa1XetIVFnSmk3xOiRTUYNpWjgc%0AvC5JkWAZiGGMPH9+aV7UwZrE//zP/9+ktJAlgGbOOvMKtoMLbiXI9nB1JdthAOdSHzLHWoSARqky%0AFUjxHCq7luOf4e0JprkUjJbSC9RkIO2nSVnEEqFd31wyDMbPcaNtDzMoqWZ8bEIb9hFEyMFkQ2M0%0ACQoXa4oIudIHLDRM2Uod9nsQsRqhnCEPmSV1rGUQVJW2ab92geiHgcvLSw6Hg9UKbTYVaK1zi2NQ%0AvzUUOWcyWroUDLWswep51nnStjv2/a8kP63yHRWT8kxnt4YsSXMxZCOHaSLn2e6pWidIz7QZvmjh%0AEPPCm9td7REOQj8OZGYIproX+0A3xEq6yzmDHBvRdxnv9CkR+b0i8n+KyJvy/ydE5F9p/j6KyB8T%0AkY9F5F5E/oyI/MDJPn6FiPzZ8vePReSPisjw9rd9Dwdf3fHw1v9TQ9LGz60X0gpLOXMR1gZrHg45%0AEclvsGMnjom0xqX1evwhalcDinyk9R4qDebVis9SKWfYbreEUv80bDecn5vQkkSTixTDqBndTR9W%0AjsX2zI51M/SMfVcnuynje0Ge0sfOJAmGjr7IPXiD9k6sXqkPkSF2FP/o6H9A6YLQx0AfQ/196GJ9%0APfYd23FY3f8TvKplHbcPWV3Rsz2wsd2WNaTxe22G3sPYViu5YVR/Bo6muqajb29vubu7qyFLpd07%0ARtfgRpvNpp7TNE1HNWo+f6pBKCD12dkZl5eX1bC0OMwpr8qNjZ+3zx+VdcFMWa3HVNc3LWwXkiUc%0Ai+ZQJMSeLg4Mw4Zx3DIM41FoOgwD9w93dF3H1dVVFQd7/fo1r169+iXDYL4F/MfA3y+v/23gvxeR%0Af0ZVfxr4L4DfAfwu4BOsbeyfE5EfU9Ukpifw54GPgN8MPAP+FObL/b53PfjHQqTyB98CWF1pr4Bu%0AJ40DrDVLFFalOifZVde1VFQfDgfrFc3bYLEbnFbhX3E5hDJ5FjNAu93MfJhYCtDYxZEsWFm/Go9D%0ASiW4BlNeS2khdoFxM9Ap9INwfjYwbnouz85Rtb5BfdcxjoYPSFz7MNmDtjAfvPNl4RLFpQKgfs3a%0AkGBtLr+OnN8OQ/2zDjh6D6OuUbBz2UYrOJUiklfEqguOE/xaCaUotbCv/T31ioCisOcFoJrqz6M5%0A0hit9QGmCl9P04TOhitdP7uqIt9dvy5MFYgN6z2XPEGQNRMWjX+iYfVYsyrbQuAbx7EaprZJX3ts%0As6x4XzuftSxUGPxmmdGmRkjU/ORxc16/Oy1KCtnU7bqRPmRizhBsnt6+NFBXojXU/vjlpzw8PHB7%0Ae4uqcnl5yW6aubu7+94eypPxrp0d/+zJW39QRH4v8BtE5FvAvwP8W6r6P9t1kd+NtY/9l4G/APw2%0ArF/111T1F8o2/wHwJ0XkD6rqm8e+V0RGoOVUX578vYK8bQbADUw59qMVrI2HjzwYXcHdSm4rBqhN%0AqZ6Cu48Bvm6YrAbTOTLl+7JwOBxYpsUwGi1kNQEhQoOL+ATzCpmxsEjPYuBsOzJuOoahpx8CMfZs%0Ai9xj33eMQ083xOZcrEXKQaxC2djFCc3G00jJZSjD0c96Lsfz4S1cy70KV7Ibx1Ls14Dsp4Bxey/s%0AcuVy67RWe6/ZLRBna9ceUlrarqzGxQ2I98dqv6c9F7931i6EGsb5fXaj4F6gncO6oCQg9l310LrB%0AAN/EOrcEqpfiGaO2bqidhzlnkwps5+8R/rEWz4qsZQOOyVDZ3MUbjKniTPPsHCvKve2ql3Y4HAph%0ALx+dn0mE9vTDL3Gaungj/wZwDvwE8GNAz9pvGlX9BRH5KeA3YQbmNwI/5caljL+AGY8fA/6Xz/i6%0APwD8oUeO4cSDcUBwZXKW4zAwsUkv+s1smbgAy2wqac5gdDe29XzcpW7T2D5JWhe8Zp6C8yIEocOJ%0Af/v9gWl/oO9MK6TvR5YA/WZkO27oh1gntHtEMcL51Tnn5+c8Haxq9+r6jO0wcnFxhgDDUI49wGYb%0Aubi8IWdbsZxbskw+oUxK0s7/uEbqMVD8eOQjT6fFJDxssQfMdXgyeVkqLdjblRRLUHXiVsa1ufjB%0A3B2rF2qudSq8l6wzOS8sizFa7VoZBpHTWk1/TCkAT9nWuRLkrXve94aTbM/Whvewhtab7Tn9aJ0H%0AhmGgG/qSEu6ql4IIQzgl6K3FnG9d2+LBuMC7lLq5EEI1XFC6LqY2O1qY0KUHt2hpRTyaMZsEbm9v%0AmQ477u5M76UfBlKGm35kTgv3O/NeXn/6itvb28LqFX7JOjuKyK/DDMoGuAN+p6r+bRH5UWBS1Zcn%0AH/kQ+FL5/UvldR2q+lJEpmabx8YfBv5I8/oSC9f8mI5rTXR9v93GX/tEyTkfiXkPw4DmpeIrsLbr%0A8BW5DZ2aczgyMD6JW7Ftz9QYEGthgq8mfizWVN4MTRx6uiImRIwFCM3EGOqKut32DEPH2EW6Llhf%0AaKUCor4CbzYDOXe1uVtKqerfrPKaBRcp1+40RHrMwLj62+loP1u1ilkN/em9aa+fGariEdYFwksQ%0APLTya12KGRsAdfUei4HJ6/bHXiZwxAuiego55xIKhbqCt5XJbQi43W7phr56PH4OHk65gYms595e%0Ak9abWg1zOvIIVVfjpxwzxgMZKSLpaLZiS9brBqlhOOuRB5VS4vXrW+7v71FVbm9v62J7cXGxevb8%0A0tYi/R3gR4Eb4F8H/pSI/JbvsL2H0D4eM4Wn2xwNVT0Ah7pxuTkORubSmkSKdqvLZfrF6o7Ic4lc%0ASE/zfGC/f6hAm9+AaZoq/fry8rJiB+5F2A1PFm5gYs7e5TCo/R9iQHJhQu4yF1eXBVMRlI5ZF5YY%0AmUJin2Y0C8NmZNEFHTtS3xE2PUFhf/fGKnhjZtwOPL3YsNl2PB8vLQzRjj4L4VBClGg/N8PAWT9y%0AvolAZFmEvKSSWdmw7QP39/d0oSMEy+5oSEfgqY8WDPd70MW1NqhmHFgfsNbo4mFlWQy8bYwHP8r6%0AsIWZagB8/+7o2P4K1jMbT4U0Q87EajysW2JKFOAiEhaB2f6HJHSYzKoyVxX+gLAdxgqq9n3P5cU1%0A4zhymGcySowwdhsuLp5a+HSxMRxHhEymFxOd2hTeTx9Ly5mSTluUqkGk89I0c5NiHAQpfaFRhRNP%0AsqNJj6PcTa+IsScUmoKRCQdUhZysp7Q3oEuVkLfh2bORw2FH39si9enLj5nmB/7u3/vbHA4H0J5F%0AEzFsyUsRDP8c450NjKpOrCDv3xCRfw74/cCfBgYReXLixbwH/NXy+wfAr2/3JyJPsNDqyLP5PKNd%0AqU4fjha4bQHeNtvkq2QtHHTP4gTZPx0WLR5XprqnME0TSY2+nXMmdBYfL0uy7BGYFyH+EJ1iQ+uE%0AMjxgsAzRdrBG6uLNvqR0LaxX4yir5l6auyj++nSbxDE42p7T8Tl/Ni/isev02HU7xa3WbR5JiZ9c%0Al896/3hfj3tJj402o+UrvId5TlVwmdW3MLZyPfzbTpm+ALlhSLcenXszRx4Lx1hR6/W58fbX5llH%0AoEinZi0yFitO6EmEaZ4qxwXW56Lvey4uLpjnmffff5+7uztefvr5QN3T8f8FD0YwDOVvAjPwW4H/%0ADkBEvgz8WuA/LNv+BAYMf1lVf7G899sw7+Rv/sMeiN+UdpLlnK2jhZqOakrK7Norar2UfLVti8Su%0Arq7Y7XZ15XZMxbNOhJLmXFYAEkBDJGflsCQOiwlJLRlevr41b2oYEYL1lU4LS7aKYf8OlbcfzJwz%0AaV4Yh4Hz83O22y1n25Ehe2jXEWOo1dJIIsTIuIlstl0tjkspoV2u5yG56MOGRgO3Uco/NTCnD+n/%0AS967xVqWZelZ35hzrbX3PvucExEZkZVdVdnVBY1lcWkZ0wZsC8kWNzUCPyCEBOpGILUMMgIBwkhY%0AtkC82C82AiTz4BYSVssWr4AN+CZ4McbQaqDLbXe56arqyqyMrIjIuJxz9mVd5pw8jDnWmmudfSIz%0Aoq2ig5qho9j3dZ1jjvGPf/xDCgyj3F/g1nU49TcqDS4Mh1Nkd/osiZjC7JqmlJCoLT9uUwTiLQ/I%0AMns22Qxwt/dtsl5cXFBnYaeYErvdjn17pF7lkOjsDFdXmtXLf865sW91ZWnsupkEv5zgChGtMj28%0ANCIAIQ6zhdDOk4VpFr67THjSa+XU0CRHGDkxnjgk+pwhbft2zKSG3Ibn6uqK7XZL5RvOt5f8+N/9%0AW3jy5An73Xdy+GzqBD+ANLWI/FHgf0QzQxdoOvr3Aj+VUnolIv8V8CdE5DPgOfDHgW8Afzn/xF8E%0A/ibw8yLyHwDv5c/8XLojg/QmY+nBjBMizRXSyxi4xAqUm6Lu6QjQFZ+xG1W/H2YXf6obUk6L9h4S%0A6mrFMCT6kGUNh6Bov2hKOIweUp6Ubp6ZgUks3DlH46uRLVtVtupm/MUllKWqN1xde+p6kgEQESKT%0AwYwLLwXm+MnrvBSRicI+e60Mi4prInYdLNaxx0x+xufBiKWBsS/Yan/7b/rOkgxZehDOubzy629a%0A2rrvexChHXp8ipphWik2Vtc1ESWwhRAIdRrBW6uXsjS17U/pKZ9iAJfHKHEeXs48UKb7W0RGEp4C%0A7hlrSIZjqQEWMR6Y3hMiWghacrYOh8Os3Yn+Ysp8nkQ//GBA3g+Anwe+DLwCfgk1Ln8pv//vAQPq%0AwWyAvwL8aynnCZNyYf5Z4L8E/ipwAP4s8Affau8XY+lq2//mmZSrgqXuys/BhDXYBSxT0lAWPfa5%0AaM6ySArO+aoBF3NTDFR+gaiVrU7wQ0Qk4JwaF0szhjzhvIg2abcJXoCBtfM0dU3lvNYbiVYRq/g5%0AkNtwkLde1V5V7grw0bJIpcFdgrCnDExptG2U3zvlxdz12t2hZv69/HhJJyi3n1IGgeU2VWD8bCyE%0AvEYDk/tZZVV4Pc55Or7rOtquw2XsTbx2BnB1Rb1qcN4TMnt5PJ7sySQYyyPKsSR/lgZmaZTtnpsE%0AzufnbryWIsQ03ZPDEHO5SI12VNBSiRGgduo5mQdr5L+U0pjYWALQfa8ef9v+ABTtUko/+znvH1HC%0A3J2kuZTSd4F/7k22+0XHXfG4iKPvh9G13GzOxpBIcZhEVdV4X9F3xzFOLQl5tvqZ23t1dVN4Mz4r%0A0SXWHsQ34BravuVw2NOnNdfHkL8bSNZ4PVotiUbNIWlPIMMCnHNIhOP+wHG/h6js21VVs6kbXDzg%0AXMS5bChJON8Q45DraNSDcSPIDbjJGFWVrmp+nFzZ0Mm8/cgpg2HvnXpdf+u28V56GXd6SDKtyuSJ%0AbP2LlONhrxcZp7TALGTS5bGJMwzD2GK2HJYpAri6uiLWSspcrVa4ylM3DfV6Rb1qSN6RvGN7eaGs%0A6XXDqi5YvV1PVdejNpF5U965O4338tyEQgajNER2LDc3N6PIfL2qiSM5slJuS7XKC54mLdarM01U%0ADLBpVsRYZ8qD5+bmhrbtqesVq5XWKW02Wy4u7gEVMRyJQdC6rjcf73Qt0tK62/8lcOacI8r0mqXn%0Adrvd7HN2Ay4xl91uh3NuBhDbhe+6jmFQ13QIasjaXrNUbad0bXE1oYeEyxqoYQTqnKtwpvwfhc36%0ADFf1I9nLSSREreZ++v0nnJ+fs2mUIxOCyhQYmOe89h22FKumUaee0XA7bZ9SzDVMCSulGIr4v8Rh%0AluRCNdAFFsCUBl1eF80i+dztIRmH7k4jtHytvG527sesFnPhblBsCFGP0lbm47FTA5AXFqn8yIEq%0APVUrx2iaBqn8lH52QhcGQop4V+Gbmu3lBdtVM8pNADSbtWb+jkdiBoeNpLe8DiGEsfuAnYvy3C1J%0AjnbMpWfTHjvN+gCbzZaqElLs8vVUHAhRzeG69pmWIaw3ijNtNht2uwO73Y6bmx2PH3/K8Xjk1c01%0Aw6CYoatW9OHwBjNzGu+0gSlXriWiX36m7yxjI8SQy9ez8NAQAl27Hy+meS8Wh9tzW0ns4tbO0yMc%0Ah0GBtZRI4gmot3NsBw59IAzQUxFcBg7Rzn5BPOIrZfg6pxWv+cYeBgWh1y5LbPYDlShwWDnPyleA%0ANmAb624yOKsZMJ+5GzXOVYgUmYja5/RsQ+wHBRSHAIX6m5230sCcctOXnkDp6b3WQymuzan/4S5m%0A9KTdo56Lm2Mwxv/QIx3vhdIgLe+dpdF1ztHkSd91HUMI+JUaG19VNJs1682G1fYMt24wJbtc4q6L%0AVTbcqezsUJyr8ryWLUfK8PzUuSpZx9a3qO97VhnEJyb69oi1tRm8tjnunHpng2MKEcWrCHzOmtV1%0AQ9P0nG8vaeo1Nwetyg6DerZD/0OoBwPzE18SrWCOxi9X1DLOtFjUcBoLC0rMpkxdikwFaooF6AqB%0A0wrUIUT6kJvMiyPmrBGikG1K6tFY4yaTXhDxkBun9SlRV1MXSZj0XdSgmKut3xMBJ0ZFb8bV65ZL%0Anve9qipCdqGJRbO5E7jK3ZjKnOVbAuvLsMlN2G7+/vLx9EKU279xyuAoiHmHgVls/1QYZ5N5aWQs%0A9HVhEt8+qxR/qepas0gC3dBzVjtCjFRMBqqua1jpMY8FjMuU9gL7KkeZgFh6cjDds8MwjPrNIkLl%0A7fcsO5cNXuY2dfmnvK9yf+85u9i7esyoincQIr72VNRstj+EBmbO4AwjK9c4KV2Ws5RQlNPHSVfV%0AMBV7z1ZfC4lsdTHjVQKJJVAXE4Q+klwk0tNnpbQhaBqzT0LMMoi5gUc2PMZfcWMjuL7v6YYeV6l2%0AagqBF8+fE/qBs/N71L7SjgAx4hrTi7UuguBdw6pZs1lvRmFqV0035sTVUP2QvndIruSOUaVDTxll%0AGzMMBbn1XknIK8Oqu5yZcoEYwwS5DSjGxX7FGDWNWnBGLMWfIHdfGGbUAksZA1kn2dL602T33lPV%0ANc1GpRrW2zNWmzW+rlidbbh8+IDtxTkX9+6RUuJevRoBaZKqz3k3KfmZuPpylEZkKkGw+3rOmi0N%0AeCnSZQti1w70fYdIN9IsbJ/0M7ovXYx4Vxfn2nF2do73NWEAwecwq+fi4h6Hw4HjIZAWRa1vMt5p%0AA7Nc0e56zy1W1mUNiGnClLVGy/aw5URISTsCTG63MCTt7xOSG1uNdGHAJa8rMuq0xyz4lETDqkok%0Av6MXUKu616R8MwWRMUwbVxoRVO3Ej6GRZUN0fzPRy1VUviZJmJ2XcpSrqXNO+0QXr53CR049X3oY%0Ap7yYL3I9gamfVfkekUTMWaP8OHsttwxh4YHOasKyMQdLIxuDdn4uFF8aRtyt9FpNlW+1WjHEMM+t%0AF1miks5UenavA8aX53s5SkM07k+1omnC7D2bC95reDMrayHk7KdmmGIYxvNT7kcIgb4LHI9HUhQO%0Ahx9CRTul5w+jS2heSd9HJVtFFVcOBA1PcjewEAPHXhtOtYOKC0WJ7Ns9MUsoDr2uDLYSSDYEXdtm%0AjsTAkHJoJEpIOrY9Ip5uiBx3kSEIm80aJzWOAZ8c5AI9kgOfSKIU85Byc7Doadue+5f36OPAxf1L%0Ann72hPcuL6gawTWeniNRIhuTdRqE5BzVakXtfNZyqVlVKyqpGMjhAOQCOs1cpUpYrWDwA91Re19X%0AKRARok0+yd4dGsIMwzB6jhKK3scKt2qv5GhGwCY1pDhghQFjOJQLLUkqIzoSa4LKiE7DQVTx7pQS%0AxICkhkO61m3nLFwcakAIUTV2+iHSdYEQvBralEZBrejMu8xeUwV1XXGQyD3v8bm1x3CIhMazqS65%0At3mPtaw48xvCoUWANuWwKHuRgmPoMjEOGQsWQ5gmsXGfDBCfzmFO0YeJ+CiAK2qJRITD4ZCNgmNd%0Ar5G1jNQLl8P0vu/Z7/eIRHzTIAKeQe+VlEhSQ4qEqMbm2O55dX3Ft77zbXa7HYfuQAwQo6M9Duxv%0Ajm81R99xA/N6pqiN8QJmF976CsU473sEt7kdJUBn31eND6tLEkIYxg6M0BNirh7mNhC63H+Yb3t7%0Afs4qk+Mkr76j5+I91sC+HEscwdLcI1U9nXZxl7wMoDCm5T7efrxciZeM3tPHehrbeZMxXd8FhX7c%0AJxmzSF/ErR85IsXxGMCLi6MxKMspYoz4Kp/jMCdxzhek2wmHpSdz6py44rv22aWnbgZKREZpBaNh%0ATAJjfsb6lTSxlzVctuwonJ2d8d578PWvf522bXny2ZPswQzsfctbSvK+4wZmyPKToWhglsOXlGNi%0AQYloAhAjfduyv7mZwqKuG4HTpqroC7GocuKbu911Ws8RU4eJMA3DwPHQEaLQD0dCMokAJZ1YzdBU%0ArTINxYGmCt3aC+dnW92nBE+fPs1ZoYzhxEnpDT8Pb2yymIbJWEhHodUikr0uVa4LGeQNfmraZfsF%0ARaYu3TYgM9xk8fnyPfU6puNdGpuTodcCu1D8ZcJiUpyOHRN68NqPSKhYdtkoJ6s9R2TyJgpDe31z%0AwwCsmg2PYqRpGt577z0evPce6+2KpqoRSZpVysCqFBN3PDeL0N3OSZlIGPGb4jPNCXnScZ+La5SS%0AgvRnZ9qobb/fczgcePny5QjelmUGyathjjEyhAQpF/nGqXzEFt4Sk7R76m3Gu21gFh5LCQCWN7JN%0ADgOBp5aYaebdwAT2ljd32dpk2p7S/Z3zJPFaTh8SfQy5etVWRK3yFpF5vD7uv0YJzk3C1KuVErUS%0AcPXi5UxDREQBxMh8spSGpjymlBKjTg5MYUvhZS29n3LVPHWe77oOy9dmj9Ptz77ud+efi8W5mjyY%0A0l5PxkZG47T0Si2Umx7fLgOJXUd33NFsNmMR4OXl5YTDYIzdgMQ0XtJJWiJRFcp9ds80TTXzPEuv%0Ac4kfljpGp86lfa8UQbPiXHvd7nejVth3p31yOZTNvbmL+SIZ9+u6YQSI6/rtTMU7bWCQqG02YmZ2%0AKoGbEKeWIcAsGwSMxX8lfduId23GWOyzRr6DqQNBCIE+KCM3JE0ThwGOXc/1dQtSc+wC3tekVLjP%0Ai+pe0AtuGY2mabhYq3jR/uoVMQWePXvC+dlWleuaisqBr5ThC7fDnE2eGDP9kmK1FJEs7p2/hxA8%0AWvAY06jSPBYixruNwIzwdodXMj4+4cGcItpNz0tg3kDbuQcTZQJgy1/Qa7Qk4BkJL28jn7vKxKWY%0AfhvvePjoEV/96o/ywQcfcH5+zna7xaFdEuu6plrrym9SDxTHUIYxy9DzdZrQdix9nCvw2bCs2OgB%0AZU+nbdtxW5vNZlwMTXJkfH/liaY/lBgTBEpbkJm+sO1z2w70XaTr5tfoi4532sBI0j+X4UMxlCwm%0AiGlUzE+537SFCinLV2KdHxPEIRCK0oASY1iu5mq8sguJAxwhRQWGO+1fHKPDubR0Wm4Nm0yQV9oY%0AiJnfUJMnJCXLE6KLCoSewGLMuJRkrvG3yXyU/JrLSmle3EkjeHs/F+d/gXGcyjqNk6cwGHf93nJ7%0At43WYn/Ers/ye7c9mLs2Zxwob1KoIjz80gd8+OGHfPmrX+Xi/j3W6zUPHjxARLjev5x5zNapb4mp%0AzDJzIvR9Oyu/gNt416l9Lc9pOfktBHKJsUix5GpZ65v9fj967X00edZpA13X5fIJ9YLOzrSswD1f%0AajL/MKapY2AY+qJnkWgzszBkLkuXrbdeWGNAGs8FmK0Iqk/aU1UVbW7PCaeBziSem/2O1fqcEJRT%0A0IXIse1JLuLcGoKgQk+5HUpIk5ZH0myCcz7LLOSV1yWOxz3b8w0vn3wfUuBsvdYOAJXDAZ6Ebyrq%0AalLit2Oz4zTwT9+zm0qzTSmpHKXmzRPJi/ZQSolD342rWoxRBdHumJ2ztH3xuDxXpbcyTsoT5/S2%0AQSk/M+0/ZM8TQbLMRAjaLkRrcoRhSAz95PZrf/F6ZpQ0LEDFs7MRTymx2W4R52h7FR37yodrLu/f%0A47jfE4Gz7RneaccFO55l+CvFcdnEtGtTYi/e+1uSqylpe5Ly3JiX06xX+LrSLFIMpACNKAZjxxmC%0ANugzbKc0ToGg5SlOqRQxBLpe67P6/sjh2I3s4KZpEDzeB+oq8Gz/6uQ98HnjnTYwXhweoe0m9DyK%0Am1TD8p/19BExSUjh2PWkIaBNElNmms7xm3IFLN1t5xwxZ42k63TFScZD0PL/lLQIktdYfl0h9LHd%0ASIdux8N7l2zP1ny6248rrFi/IvsekyEpcZcym3F7W1IYFwWRrbdqieOc/JuFLFOq+ZRRKcfrjPSp%0Az0+vya3Hd78/f2/5VwKpyb6zwG8sZNpsNqzXa/VM8rkc+VBVNaajU24vQ+764KXwTsZzMu2jK4Db%0A0iswbK3cV5iDwKU3bV6MeSV1Pb/2KalQt/X6guk+qXw1ejCllxdCZLfbs9sfubm54XA4qDck+vt9%0AEzkcfnCSmb9pxm63o/Iy1mW0bTvrZwRWa1GPhsPqi66vr2+lHktyFUyT0vCcUhmv7QaObU+IAuIJ%0AOMT5nEFKpKIY8XVjmsQ5vYzn4nLLqm54/PgxfduxflTjnRoE512uzJ2MnWWMDPArQewYMzcladho%0AYZF5MI4Jjykxg/F5yB5PgcWMWEWRcbgdzpw2PncZnM/77NKrmW+DgnAn4z6Vi8IInJ64BmoAtMXK%0Ahx9+SHOx4v333+fi/IJj11J1K+7fv49YeUiI2qhMtJbNrt9o1FO6ZTReFxKWjGcA5+cejP0fQhip%0A/MfjkbZtucKNXRDMOy57MpX3eHnPVZXX7gXO06aew0GFwHe7nbaOff6UoY9ARYqOm+sfQh5M1x/p%0AB61WTQT6Iat1xQzqErQX84IHY4bIUm+TJQ+3LkTJ+jUjpECwudYQw9SoyFb+gAAAIABJREFUPkbV%0AgtFMRl45X2NjbFIYS/Teeq0rUNfR9UealfIZch4g38zzG9hCpBLsnWECYR6WpJRuIy1RPZvSa4GC%0APVoIUZ/yYJaG45bRWOInzI1M+d5y9Z8My91ezfL7p0I2G5NBYDQMVp8lIrR9x/XuhhBhe3E5pv0B%0AYgwzAH15TPmJbWl8zwxc6ZnctX+pvHb5eQL1qEDxomFAb8J5PV0JJBsIbz2/3MpT9rcyL2jwt7Gg%0AzWZD5wZCEGKQk8f8RcY7bWCAkbFYtuk0XMUyIZVPM2OhMguTgTHDUeqV2sUyspLdsG3bcnNzw77X%0ADgNVvaZtW46tCvPo5zzizKClOw2M3XgienOfn59zeVbTHVuefPqYw+HAdq29nB1hNC4ux/+lfIHd%0AVEuANyXtaTwbOb1qoUFpDEoPJsbTZQM2gbkDd4HbBuZU3dKp75x6v3xt+fu335uT0sbtW1jizHBK%0AvkbKpF2v1zjnePr0KXLm2W7POd9e8uDBA1ar1aQH1NhkU0/W1dVs+ylpmrrcrzJEm+2LTB0fS7Kj%0A0QqW3o/xWixTeHl5Ce0kFFUWxY7Gsm3H++LYt3hPNqLai7obAu2x5/r6muvrm7FVyc3hBsFT1xvk%0Ac7zw14132sAMXSCuyAI7ifZonRuNPFXniTh1XQRIyWQE1VVUnoW+1vY3anx8g3MVu11PVdWELtJ3%0AkdRXSGjYtRHnLzgMNUMSro971XsVra4l9NpIPBxx1TkkbWyfokN7EQUc0FQV9y/OWK1rtk1FVSfO%0AL1Z8/3sdl6sG+o6mD3gHTe457TJ71Iuj8hWhHxgk68KKw4tiBC43lY8yVX0DIDJ1TkwoQ180xEsp%0AkBBLxEFSKQgXhTgkZEi4qMWdfbL0v0zGLq+QEZ+1dLPEwFJfkyIVXhgEUC9BxI1V6jGi5QApaSgk%0AgJ84LTi0DiyLU0UCQ+zViHpNUWuvICah9XyMNvkq5xGEla+Qaq2N5BFC6BmGIyltkEoLS3XiV9RN%0AjfhCAS6p9EVIPV4cQbQvUYa8dIz8Ez1vim9pmxlGQ5KlPeKE36RkWJCnrs5wEkY6hXeOvjtCpkQc%0A9lM446RBSAz9AFJx2Lcqreo9MfWIOMQFjGskeLyrWbk1Qx9Hka7qB6HJ+5ttmHW3ePtwOIyPyxXB%0AbuCyvevZ2ZkagMzMtb/j8UhK2ndZJSg911c70qAXXJXxBqYFKYw3QrnoztJ7Mu86aCCrR41N27Yg%0AOQW5afj000/59e9+GxHhbLsduwUsgdwS0D2VRhwxAOsUWKyGIz7BPBSSEyvtXef+FKAxhZPMjIYV%0AUZ7yQG6FU9wFFp/aH/VCxveS3PptYBLCKn+vCFMs05dS4vLigq997Ws8ePBgBEi995mvVIZuqoE8%0AhjtZo3fK2qmBLbEt5USYR3gbwE0p0d50+Zr64hq7cf9KW105UwWoxtA/pblygFbbe46HK+2BRKBq%0AdAFFYLVasd1u2e3bXGJS0x17qioiUhGGRNfv77wXXjfeaQNTgnkltbkEaW3cctmz22pNy21ihKDa%0AuMGF3BVQjVVHZIgDfQgM0fAVgMhdXe/GyT8i9jlUkaihjihY6zzaaL721JXj6YuXvHr+gpUI69yn%0Ax8mcVLfkWSyfTxPg7jore1zurxMt0LOSgpGiVjx2IrkIb1p47S8GlYSQmL9jq7XcNiZ3GZtyjIZ7%0AYZz0UOw15SGllMU0o07e5bGVGR5xbgwP7dobDlbX9Rh6X9y7nEKcIlNk5zmkooeR7VveL5fSvGbz%0A1v1hRlOTASNulPs3OlHpCudUN2gEbhGc99Te08hUMFkadHtc7mtVVWO457wKw3f9QFWtePDgPZCK%0Am+sjx2M3Y3S/Zp353PFOG5ghDCPzNiwyGnbSYer/Yies5Lnc3NzMDFQKEcRrbVGIDD3UqzX7Q6d1%0AHq8OqvQVVeQpytRJMKWEtnfIeInLWEYKxDiASUY6BfBD7KmdsKoqVmvtwFg5x69/51tcvXzFj77/%0AaCTO1QK+Ei12rFQZvvJT/x2bQFbkZsdqx68hY9HSlazSl5h9dn5jzVPBpcG6y7uZPjs3JrFYdpcG%0A5jYgexcmU3oniSAJhHzuJ/GpIYZscLR3dCThmRsyxaoEX1U6k5n6RxuP5OzsjK9+9atTMkCm7hOx%0A11RxvZrqmEConIbcEhMht9b1GWy1MXq3+AzYay3VeA1kbiyscnpKOEy/Y7wl0IJF+4wlI8rz1zTr%0AUez+0Km3s15vOB47bm7UQ7l37wFNoxKa/SEQBxX2iqfc1S8w3mkDA5OlLi33KZCvNDo2yexClCns%0AGEEkEoLyA4YI8dipxGb0kNXprGF9lJh5L7qS2ijTz0gca3+EiEuqai+O3EpC28RW3jO0LdcvldRU%0AeZ9bjuaJ7ew3l61Npu2dSkvGMBX02Wcn5u50HnVlvzvcWh7bqXEqJSsiY63O8hqd2kb506c8mNv7%0AZIYQyoZj45ReSGuOIYufy1iOWsibDZeXl2MR4Vj86ibeihkl6xeknoUjecndItQI2qGYFnPemu3Y%0A7DzqdVXx9/Jc6v+L84GBxLodMKNZsVptqKqs9xLLosWoYRFGwKxHs9G2LYej6j+XpTKaiUpZKeDN%0AxzttYJxMxgIm2nfJ4JxU7jTWLJ+bqJTF4CFoH9+UUJWwEBEq9v2R55/d0PUD+52m/LoUWK1WpAh9%0A3wEOK7IrU4QALiXERRrnSEFvosoJ4Fg3FZt1w8X5hr5v8anj5vqKi82GdaNFj5XzudvABEo6L0ia%0AjEuZQSqFt0th86XnoftXplIjfZ9dfiu1yOnrOOQK9ahgcegHLbpMCRJjmcb461FjprHKON1tYJbs%0A3qW3IhkoHb2r/DuCJ2RNE5JjiANh0DB3yOlbktPVN04TxrI3KUWGENhenPP1r3996oNVVbx48YKq%0Aqri6uho9GzNI+nxqYO/F5eZ1mm9p2579/kCzqkiZNV4S7ZwzQ5rwriZk8XTzUqy0ZTyV+Tja9pi/%0An6U4ECRnT+1+6/t+9Fwss2rvV64mhAHNWjbAwG7f0rUD7bHncDhyOByz8HlF1Qh9l8CpV/g2442g%0AYRH5AyLySyJylf/+moj8M8X7/4uIpMXff7P4jQci8vMi8ir//byI3H+bnbcsQhkezHr9Ft5NSb4r%0AvZZbzN1FZSk41cVoO/pexZhClJwNKFbVz0HZZVyBgopOEca2IcbcdCSOuz1NVdOMzdSjGhMpvBc3%0AB5FngPJyu7MV8vVhTfmZ5WdLj+mUB3OXR3Lq9S8yTn3n1u8vPZ2oRjvYdR9d+9v1Qjbu3dNao2fP%0AnvHJJ5/w4sWLsbanHMvvjliYGdAizLa/rus47va0+wOHw47jcT9yUgw4Ln/bWrKUIP4pblMZPi33%0AyVqwOOeUPlFoH5XhlS1EbdtOBNV+khm190u93rcZb+rBfAz8h0y9qf9V4L8Vkd+eUvrl/NrPAf9R%0A8Z1lv4M/C3wI/FR+/qfQZm6/7w33RVXrUhpL1c17sAtgaWkDcrfbLVVVcX19PXo4htxPjyHlOpUU%0AHQFH1ydudi0pOnAN3dCB09acpJxiLHo6p5yB0ug/4AT9PwlONO3oBbabFffunXN+sebyfMOLF5/x%0A7W98g+16w73zLY2vFHtB8E5vwOSE3CCBxs9rkZZZM9uf5c1Zho/mztsNa8CtS7pdFQHM2jEkUi6r%0A8AhBgRZSSKPHMqZgY4H8vuEoPZhxn/VoFq8pmBuygl6MkT4m+l5rbEJQjhFEbWhXeHAiyrKz++R4%0A3VFVFV/96lc5e/SAR48ecXFxMctIWt2STTzvPYKGE6HriWkg9APei/ZJkjRWMk84GWhiQIBB7yHy%0AYpkUO/PYZxXcjeiCtjm/yHwX5XHtjy3eKYs7RSEE1dw9316qRz4kutSNeKNb28Kr1IQYUhb6Fryv%0AAc2itseeNnuDVbUiJuHY/QAkM1NK//3ipT8sIn8A+J2AGZh9SunTU98Xkb8XNSy/M6X01/Nrvx/4%0AayLyW1NK33yT/THjYKDmEkg7lVFZejZLIFFvQJuokX7oc5qvYkBv6oggxeo89wA8wrLc3jIFFsoI%0AVW4tcrbZcHG2Zr1e8/Llc549e8ZZoytQ5TU80n3KEwsLJzQTsKxDKrd7yssp309mIF7jwcxxgHTH%0A320P5ta5ecNMxDJcOvVaTIpr6fVMKmEa1Z2ftp1GZqwa/7k30rYtPlacXZxzdnbGdrtle35+q1/5%0AXaNtW1zKsh6xZ+h6Vqua2nlcPeFh5TVQDyaNxmU6vpz9ZO4l2nWCqWDXwjxroAaTtIjt79nZGVVV%0AjcTSNHhimt+bh0NOWuRQuqnXkBx9G4mSGw3CLMR7k/HWGIzo0vAvAlu0qb2NnxaRnwG+j/ax/k9S%0AStf5vd8FvDLjApBS+t9E5BXwu4GTBkZEVsCqeOkCoGtbVk3Fer2erdiGyxir18Kjkthln7WLYxcm%0ApSnr1LY9L14d8NUqryKedhgIUahEVwFbWeeT2C0mQxqFiurK0VQ1q3XDo0f3ubw44+ysoa49f/ub%0A3yS0HevtNl9UNTJ17XGStAtjpQbKWp0YPjDiBMwNjN5stpdzDwZQMlsBktt5Wf5/igowhZbl7942%0AQOPGv+D44h7MdCwxKvYShqLdDD738faILJqzZQ/GJqM1q7N6LpuspXq/tYeFCb+rxU2hej4PXddx%0AczhSNz5nlRIDk5Fp6vV47YBbC2EcFtyZPCbdF2XqbrdbwuAzKGupbpWEtXvbuYr1+oy6Duy6GyWD%0AEmhzse56vUakJ6WbnNiY6u26VgWnSI6u+wF1dhSRn0ANyhq4Af75lNLfzG//GeDbwKfAPwD8MeC3%0AAf9Ufv9HgCcnfvZJfu+u8YeA/3j54jIWvUWRLwoUy7Dg1o3G3DDBVN/Rti1VzKtFTKM0wzh53mDi%0AlGCs956z9WYiTyVNmV+OYlHz43KS8vfmPJjytz9v22W4MmFHJzI+i/NTTuplSvmUh3FrG7+BUf7+%0A6deUFmCvn9rm7FiYn6u+76mkHsst7t27xyp3DRgrq0/sh+EoXehGTycMSta8f/+S7qDYxygG7ueZ%0AP9uH0gMd7+cT1zUlZoJQdi+ViYtSRBwYIQKro+rJ+5rv664bePbZC7pu4OpqR9sZNlRT+YbBZTwI%0Ave/eZryNB/NN4B8E7gP/AvCnReT3pJT+Zkrp54rP/Q0R+VXgF0TkH0op/WJ+/dRdJ3e8buOPAf9p%0A8fwC+LjKpCgjINlFN9DKQK+YFFjrh4O+3+2mDTtd7XyV8JXn1bOe65sDz18d2HcDz57vqKuebgBJ%0AgRrwkuhczZCg8hXOQehbXKbpS8ypawJ1ElJ/ZL12iES22xXnFxu2mzXvf+k+21XDxnu++61vcxYa%0Atk3NWbNls6ponNBk41KJo5IKiQKpwrlpUhg5zKppTSrRbk7vtNp8CEcgE/68nrMudrkfQF6lw5Sy%0ATynRDl3WEongRdvwRi17IMSshyxZVTCDnahiGpIrt0WoohrlwRaElOhz9mQq7jM8opzQCWP3x6xY%0AGJMWlPZRu2CSVsQUabsjMeZgtHL4lEgSiARinb3KnLLWigZhddawajasVittRTIMyP4A93N9WhhG%0ADojDIUV1OUAbVOHfoeHEet2ARC4uzxCXcjiTcK6QPHUOk/cwuRDNLNZIJXQ+Z9dCEbYbG9t5bYoG%0AGcw+Um189rhbBgaizw3j4pQh1doxYVUrCNyszzgcDiQc+2MLfs3+2PLs5Xc5Ho/sW72kfadekzRv%0At1i8sYFJKXVMIO8viMg/DPw7wL9x4uO/CPTAb8mPPwU+OPG599GQ6q5ttsDIGlqi6eVkKlH8ZVUx%0AFBT5wiUttkNKWsS42+3Yd5nI1w0k0R7SdcZ7yn25FS/f3n9AV6CLiwse3L/H+fkZdQYLD9fXfPrp%0AY1yy3kfqWnuf3dzEWKRXHr95QlPHAT8LgWwlW2JN07GWgG8OK4tC0SVWdZdHMv7WXRcwfyaUnhCF%0AF1ReHwGZeUfF/xYSUeJlzPZTHYDimssy5Cs91ilTYkr8IQRS12kmCVhfbKlXzRhmn/J09VxP98J6%0AvSZ0Hb4SVqsVMQ4jj2S6X243pbPjnHCbEj9zRRvjSQdo6Ods3fJ623kxDKZyWXlAIpLUINoCMM9c%0AKVfG5CFKL/ZNx98JHowwx0fK8fcDNfA4P/9rwD0R+UdSSv87gIj8o8A94H990w2HXAFdtuhYdmCs%0A65r9weo+PH2vzb+dU4FtA1Dt/yEE+iGyP7YcuwBJOPQ9dVWpm5j7UEv1+hBluliOVbPh7HzLZrPi%0A/UcPOTvbsG4q4tDj3Zq//gu/wP/9f/0ij+4/YFU5ai9a1MhUPa3/W2g01aiYgbFq6tKYGHAHt8O5%0AMqVqny1DyvIczifw7b7Rd4VI5RgWHg4wsUMTo5dCYizKDIXpCRkAtRQ0QMos6jCkAmsrOyWqB6Vu%0AvmEI2YvwHhE3NlFLSTM+V1dXrDnn/v373HvwgNXZGW1my45tVp0n9sPsXFs2aoiB8LznweUlzqk3%0A7b2MxsvKUirfqCEqJUJkGfbP76+maW6FaiIy4kUjY7tYaIDRO+vbgZv9jrY9MKRIN/RcX++43u15%0A8vQVXRvw9YbL9Tn4I4fDYbyubdvzNuONDIyI/FEUuP0IDVP+JeD3Aj8lIj8O/DTwPwDPgL8P+BPA%0A/wn81byjf0tE/ifg50TEPJ4/Bfy59IYZJChEmotRZpKW2IE9/ryMSPn9IcWR77JcxZfey6nHGsY4%0A1s2KzWqthiBpU3tpPEPb8dF3v8PhZkf14AHVrO1ozHTySdDo1N+tcn/mXt5oYLitX1uOu7yv5bGf%0A+v+LrHDmuSy/ExcBsoHRNuGS3PaAUkrKoo4RU8U/dRxLz3KJVNmidDgcCCGwXq/52pe+NJaTBAc4%0A9UROaR1PRjezZWNgCB3nmw0xV0A3TUXTVLPPB8rylWm/T2Fpdp0Nryu7AJxa5Iww2LbtbFGomhof%0ABg3Xolb0V76madasVz19d8P19U63kXHH34j3Am/uwXyAcla+DLwCfgn4qZTSXxKRHwX+CTRcOkeN%0A0J9Hs0glBP3TwH8B/MX8/L8D/q232fkQ5wCugbIli9U5lzMLIChvxUk1AmPl9wH6QUHcISaObc/N%0AdYeramLqM1+gaNZ1YpQ0fe+NnzIZnVVVU9WOikR/2PP9Z0/53q9/h/fuX3K2amh8ZFWBdxHvNFvl%0AxsLIrCQvAllDxtx7w2HKFXEZ2mQJ29lrd4HDZfnE0qspx3JFvWtEpqzP+DylmXEpzII+TiYZASGX%0AZqiR0venlXte4FqyhklTFkwnSyyuUQZnSWyamu12y4cffsiv/MqvUK8a7r/3Hhcbdc4tm6STb94J%0AwDlHbcYnKfepbVt8mDwXA1ynimjtUFBmQO00mgeClPSD2+G+LYjm2VgoZFwd85D2+z3DMLDbHVhv%0AzzhfNewPBw5dzyfff0LXDtzsBvbHgZh0oRq64+gRL1vLvsl4Ux7Mz77mvY+A3/MFfuM58DNvst27%0ARsiUagN5bZU5HA50XcdqtRon39huZNHCxAyR3YAinj6oSzgMOSwYBrxTlfauHahrNTQw91Rur2z2%0A+3HESdr2SBgEL4l765pUe0Lfst1skBSpnYZFPns+t7ktJi41GblylbYVubz5bT9OGYfpu/PsWdkw%0A3rIXS29mEuOyMMRU/iZPMBX7mFLS/lFJiXhSeVzKNVoi2gYkTaUAwcKq0YMpjIgRA50jxmHEnOYY%0AjBqi0vhUVZYUrTwpUxJWTcOHH37I8Xjkk08+4XA40DQNm81GF6lCBU69lETK94xlBVe18lNSGBhC%0Ax3G/Z3OmoVffD1RVs8BvJuV/W4DKhUH3fhr23XJhcM4RC+NqYfJutxuvT0nDGNKOq6srmqbh8vI+%0AVbPi/c+uud7teXXzTImJeJzU9N1u5NikKKxXm9sT8AuMd7oWaQ7eMdZhmAUfhoGbm5vc6FtTfQqu%0ATWk/79Wbubl5lT8fGYaI8zWJgSSOmBwhCSRRNXmZhyJlqtFuGs1i6X4Zx2LTbFg1NZ6Ek0C7P/CL%0Av/B/8MHDR7hhYO2gEr0oPlfk6l2mdS4pJcgyEbHQ+z0VvtlYehglnlK6wCUHYhl2vu639fjnv790%0AaDTMUTzELE4wD2YRKsWUcMmukYpICeqxEadUc+I0WfKuYdfIxLDFq3jUoy+9TxgS3/jGN/LEu+Qr%0AX//a6EVU3iMFtiUyhbDee4ag99vZuqFpGtrDvHjWPJ8SK1Ty2hRujaBt9ljIi4r1LbK/U/hYaXTs%0A/ZLZbvsZY6RebfnsxXO6ruP7T59wPLTsj8pQ355d0naJFy+eE5Pgnc4Z06k+7JeE/C823mkD49zt%0A+LCkdpfuva0cY7iwwCzsguwOLV2vBWFawGgyAIrkW5i1jPNPsYbHeo6qoWkUTFyvGyoBL4HnL57x%0AvY8+4v7Zmr47an2SqzHWr5CB6ATWVgObkCe8keU+nQ5n0q2bc4aHnOC5nMJhRGQMP1Ka82zMqKmx%0AkVu/Y+BtKl43L2V8HiNDKoogLUNCmkKqE/uV0jybZY9jmmumVJUfF6GrVzcMSb3Mr3zlK1xcXMwk%0AMEo2rv2+9Y8uz5m9X4boy2sxyllmAzN5zif+ToRF5RCR6bwU181+1z5jx4LzI6D96uqam8ORjz76%0AiGMXSGlFio66WdO2PTFOjODstL3VeKcNjHfzlPHhcJjpkpqBsSXVCr9SSmP6bbkqXF1dcTi2pFgT%0ABW2BkoQhBnyqwVcYP6M0JOQbZrvdArnwbFXx/vvvc+/elnsX5zRNhfcRlyfOr37zb7O/uebLX/mA%0AtYeVdzS1144ZSVPHRCE5nWAaWujEkwHQVjuzSVkCzeV7OjESVrNTei+l0SiLQu37r/MU9AY2jsmU%0ArRp/d/yKjMal3F8FPBNSAOl9MFwsGw0BmEIk0KxU6XUtjcy4//b5omK5LOL7+OOPITl+++/4SQC+%0A8pWv4NbNSLOfX2MLX2RUArRzaC1C2sOBfmhzv2erip6q2o2fJRjTVoWfTo05zWCZ5s60jDjtny1y%0Adh8sQdohC5b7umLfHnny5Am7mwNXNwceP35F30ec29A0Db6QAjX44W3G26v5/iYYy1V6CXAuJ9xk%0AcOZxeUoKkB0OB4YhcDio2ytM6T7Tcl2uKPb8Ft27SOvaRQ8hkIbsUcXEJ598zCqrpxl+JCK5dxOz%0AZeOUV7F8b+nBLMcpr6Tczy/Cd3ndtXjd58xL+bzfO+UxLfdz+AL7emr/SmPUti37/Z7VSluSmJD2%0A1dXVSGBcegIl1lV6gSIy3j9WQnDX+Sk5Rnddo1Ne+V00gfL376q8Hg1334/YWtNoSPfixQtihPPz%0Ac4YQuLq6om37GWUBpszUm4532oMpR3mxzfJPFn26SW1YKGXfsdJ2i52b6nZ4YWAkJy6uhQml3kyI%0Anv1+z/n5mr6ugEjtVGzKO8+zZ8+4f7ZhaDvcaqXaK1nhTGztFdO0nfZDj/X156F8vsRgyseTS387%0Adb/0cMrvlMc+hkOL/Ti1P+P7d3x2KTFp4dHMwC6O64sYmYkjlLOF/UCMiQ++/CNszy7G7MvhcCCl%0ANHoXKQ7FcZo2y8wxU88k6+jEYSCmOBP3Sonx98p7rjRgy+N43SIyP97phFkod9c5H4mZTc3Dhw/p%0A+8B6u+XZ05c8fvwCX62oqpqbm5sRlLa59EPZtuR6d8V6VXNxcaEputCBTBR09TwTbda5qIAYAj4l%0ACAmfYAiCj2uePznqKtR6ktuwayMhCgmHqz24QJSWgFembbXWC+ZqJApDGEghsam2xDjgCKxyn6O1%0AdKxdgw89coAQBp5dv2LrVqyl4f69Rzgn1OtLavaquepqlXNESJlC75JesI13ij9VjugzHd+73CI1%0Ay2XaSUqJmKaUvGXKvFNafAxJS/djZm7m0okhZMZKHHL/bx2V+LG4L0kEyQBxDEgOPUPIpQR6+okp%0AjhXOI1aT0KwR2mwuxUSI+laQASTr7JJGketS8yiFpN0Vg/byBgpDaUS80kGfwp1IYrXdsD7b0Fxe%0AkqqKx6+es9ls+Lt+9MtU97b0ldDn/lplIzMLrcfK5Tiw8hXr7bkKhq02DENHill3OVWk4Nh3B+q6%0ARhqvYHYYEOmIQVUNbSEUEfTUJQK5o6QrBMySG8XFVWXvdjbRVbUWRMpUmJlipFlFusEzDBFfrXnv%0A/a/yEz/xO/j0yRP85mO+9/j7vHy1YxgGDmnN2WrNWb1i1VRI/CH0YMrw41T2Y3Jr5ynYDBIQSfTZ%0AYzm02inv0Dr6PpC8I+QKaCcVSqQC0kJkWzc0pmlBtANBsjTq5F6uViu6/Y5NU/Pxxx9T+4qzszNg%0AWuHuGkts5XVjiUVIQtPCuvTrnz23hmv58alV8vM8hNcJW7/dmFej2+bL15ap95KEd8rzslOn4Ckj%0Af2jkxGQwdFU3tzojliTNsgTFOYfDjVlC7wWJWvU+9D1GvosLWQXbt67r8r1l++oWx1l0LEiGgd3d%0AX6rcz5TSLe8jJEuAQN8f2e+PXF1dEQM8fPiQYzdwbJV0WNIjlvPqTcY7bWBEtGG9VoZ2M6o0MItZ%0ATb8lxkjIaetaHEMQ+hDZHzvatqMf1sTkiNGRcCA1IhUxQAwOovIEaldr8SFKpHN4xCX64yGnyaGp%0AtGLaieBSpGkahsMNIQR+7Vf/Hx4+fMi6qfBO2KzW9O2Bu7A0y0iVIN6psbzh9PlEJiwzHSXJcPl8%0AmHkFp/cpZ+71c0yhy6zOSBgJdobDGE9mhJpkHjKV+5FSIX0Zi5qpEOjzSt7l8EQZvzJCV8YAzndL%0AvmfQFrB1haus5Ydnmyunu65js27YXd/gnOPy8pLaV2MRaMz3l/ceL45mtWKV65hEEu3+QNNUpKgt%0Ab2xyqiyC1rnd3NyQkr5WV6vx+opMYb3t87SwTEWSBj577xnSPNSFqYp6zB6NF8zRNGu8i6R04Hg8%0A5sSI1jidnZ1zfr6nbXuev3hF7Ssuzzas64bzzfr0TfA54502MOY+uEzLAAAgAElEQVQ6WvV0SXwy%0A11aBqozP5IsXooofRxwpRULUftKavUAri3HElIvSsoSc5HqmXFerfAggxQzMjr2f84QKkaHv6HtH%0A4x19vpCvXnxG17W4s4Y4BOqN9hZW1/i27sYyXfo6cPN1wOHSszkV158CWL8IU9eGGZffiFcz7Ut+%0AnEqV/blioVYNT+cs5F5DSSYeCaCWxTskT7rS4FZVxWaj2RNT4y+r02FKIJRMbZg8T82+xcx3MZ5M%0A3n7OJts9eTgcEFHdGe8mz3tMh2O7fLpsYMYWZ6JfLLEz88JsbgwhcOx6hl4X4vV6wwcffMD1zYGn%0Az3cM0eH8irOzcz766CMcU0go/u1MxTttYAzpN0lMs+pm4fd71UAlVoiDuqqJIdAm4614hpBo+8DV%0Afs/h0NKzmjJCIuAahhBwSdmzgsMlT+3qXL6vMb8CwIkYekgJ7yLEQSnXZ2tWq5pju2ftK7773e+y%0AqlX1rPLqvQxDx6quIbUnj9WM6TxdHOd/EqfG6Rkwxvj2KakDnkMkyc+leBzTZGTK7dzlwUTJf/m5%0AEenMkxHJ3RZJ4/+S9HMxzbNKmQ1g0k3ThJnVgem5DkFDpK7v6WNgsN7bosaeLAzlnUpO4hw+G4yq%0AqrRgEqbWJtYcDaU6RBLnmzPWm4bzzdkI3gO42uGRsd+T9/U4ic1T3O12GeTVDGEcgjIoYWRJm3dT%0AZmrEFqbx3JdhnxmfObBti09pYAyvsYTD2Eo5Ql01eAfXnzzne48f873vPeZm1/KtX/+EZy9esj2/%0AT98PNI1KfMQktENgE35AglO/mYYZl5TSWJdj7mtJbVdRbV1pmqbh5nrPMESub15Ctebl1TXNesP+%0A0KvWrnidbNaBL2qLESW+2YX2OPF4q08JAaLuRxxiLnLzenMBq6ahFke7v+bFi+esVtpVUqUAOmrv%0AkTSRBMvVy+JhW22NHQrTRNa0+rw5l6VmKcIgYLb621hWU9uNqzdnQeQqsI/kCoJeZtamYgKUnBc7%0AnlHOMiqBUWRu2Ep334xL35cN51Vgagy37Bob3V7Amxcr6jrUlar749yI1fi6GiejiUqFEFg3DZuz%0AM87Pz9lut+P5XA7bx7ZtSfl69P0wYivZrrHf77WwtZ4UCFerFSJqBOqK0WOq69V4ffS6lyS6OJ4D%0AY+a2bYvPjfnsPhm3n/fZOpY65xBXZVU8z2azYdVsaNuWV69ecXZ2xgM8H338mO12q2FnShz6DifC%0A6uGDLzotZ+OdNjA2CUyj1F4riWTeK2ZCnBTuRISXr67phoHkAi+vrukHSL5iCAFczHKYAqkCl1PH%0ALuFzTyKsH01WpPQRSnBy3dRsVw3bzSp3D6jwlefXfuWXuX51pWLeTW7+JZK9jdvHdopfMv6PZnHG%0AvzQZAjMwMQacNZqOE+hrz1OM+pdblCzjeQNZlyHU+JgC5HWTO2PeiXkl+lkzRvp6iBGx9LhMHkWK%0Ako3LlD5Xyno2LAFiTHSDSh8MSYl6zrm8Xd1WZZrFlcdlQNf2O5pxYwqlS2wlhah9pvthuo+cyp1a%0AOxARRlrDaqVhbqwHQujpu24kfdZ1jV9NhalanJivs2UIS+A4t0Qpw0H7jPWfNm82MufJ2GJrcEFd%0A1xyPmiENUaib9UiFUP7Plhhf8c1v/iq+0do9Iw26XErjEfrh86kAp8Y7bWDGOLSIq83A2OM5fyGT%0AjULWHO17OoT9saUblBcR0oBEn2t9BLCygYgpronMJ5pLqBC4cuf1wnoDZXPWJgxIVfHs2dPs3dSF%0At5KQJDjuBm/L473zvcLAGED4OpzFHi9j+LswmHL7NknH5zk8Am4R6sphYlFTGBRzaHMXFmSfd6Nx%0AGTGYsap52q7Tni66mruMu1QenIxKcMIUXo/kxkyuKztl2n7Y+yWZrTwfo1HPjdlgMhjr9Zqmqkme%0ASU+mqnTBEhnxpbvwlhLkVVoBOcSyXtenFyPbV6uyjzESE7klCyOZ7sd+7Mc4297j06cvef7yhv3h%0AQNcOuCxcLt6xalY/nEQ7tdL1WK5uN54xdi2k6I+BfujoW23Edn29o+17Xl3vuT5e8/LVDd0w0A+R%0A4HJ7V3EjCOxJOSOhz1Mc8MW/JAkvyrtxVIhzNHXFqqmonMe5HHt3WvuxXTW5o2NFnSumTUke5jdM%0AGWOX2SN9LYx/Rje3yuJk2TSZC3HbebPfW4ZGJYA6TXY5MfFTIb9QUNetB7Xd63nyh4WRO9WK1DJR%0AuhrnjFA0lbqUKQLmzfS0fY/xeiCpUXcVUpnKn14LX1UMMLZ4dU61bOscSnvvRzbvxfYcqScVN/Ne%0ASsDXQisRQSohBkvtwrpuuH///siDqeua2lf4VTV+10LTpmkQJswwhOn8wO2MUoyRIYdhI9bI3JiY%0At2dwQEqJ7XbLer1mt29BelISvvfpZ3zrOx/zjW/8Kg8ePuInfuK38f2nn/Fr3/p1uq5j37d0bUcf%0AEqv79Q8nyFu6rmX4s4z7p1YfaQTZjCq+PyryT3KTgppL2YMhrzAKdsVoE3puCBxaL+TQpmjOayP7%0ApmloVjWrVW6EdVSq9uryQsWkpDQqc9Du1LhrpRsnbpq/ZsMlDSlMR9Z0YO1/Qhyfh+Vv6l7d+s3Z%0A9guOCScMx8n9zZ9PYrAlgGVA9HfK7ZVcDL2GcwlLKLpeZk9ECoPi5TaNPsIYstR1jUM4Ho+sq+3M%0As7PfttfK33Fez45iG4l1raGYkiRjLmyUqb914ZkNw5A7dto+5e0VrNny84rfTFyaEALxjtDa5oSd%0AN6u/SijPywxQ13V88r3H1JsdSRQfCiHgwryt7hflYC3HO21gYLLeMHf3LVRSax5xldAHYWDDy+sd%0AL68S11eOITS4tKbdvaSShirLIRi2UF7AlJIKfeNw6YinpnaSGaYJZx5MSmxWG86bDT7UPNyc4Uk8%0A/vT7XDQVG+/xSahTokL/XFI8JNSJmEW+yWUFiCrNa0o8EkNPIOKbhpSEPiZWTgFUXBzbJseomY/g%0AHJE4smtjivQMRCJt7AgpEAgq4BVyNk4cwfgzMPUfMh4LiUQ9ii8F62zpsuxAzB6SYTkZc0koIGtt%0Ab1OwvBF4C/Gcqq2REmlIpD4wDJFjDOy7lleHA+Id9fo9NUiWe/JrqARfaUW6c0ZedPgELqqn6UTw%0ACSRE1mcrmqqmO7a06ciDBw8yR0b1aruhV2ypa9VrcEI39NSZs5JIJKeFHc5VtEOgomKdRb6req1e%0AdTdhJN7XOD8ZLANhjQsTLcbM/7limnqfDUeKOBxDPC1lOQvhs3F0TUUKAyElKufZrjf81h//e3j6%0A2Uu+/a3HvHj+kn7QTFrdCCnLe7ohEtrT2c3PG++0gVliC/barYIwAdLUmc8IRseuzTF+IbcgE+uz%0A5C/YmLIx9gfiDEDNK5qIhkBNlUWfI13Xstvtxjg/dorJ2Mq1rBeKaTqGu2LsL7qqnMY2Xs+ned1v%0A/Z0cJXGwBDS1Fe9U0RtSHAsJnXPFRZqybDpJT4eZ9tqp45i4KUqEOxwOXFxcjMBt+Rt2PezcmWyD%0ApcANYC2vm/JkupkXZttfHndK1vHg9tDQKs2+W/p/5TmFOdEuxqgeavZqttstDx8Kjz95ru1yLi8h%0ACR9/7/vaXSEcR1zKQq+3Ge+0gSlFq0tMocz/W7q6awO7myM3u5aPvveYvoNjG3A+gZ+qZ4cYtJKA%0A7PpnoyQ5Bu66Do+Q1hWgIK5SujWt6JzgfAQJiAvUjXA4HHj5/DM+/vjjkfEpAr6aN9fSm80M2BT+%0Aje64TELfo+vvtebEQrUYc/iRGMsVUpzKKew8Lf9KgxMLADegIHUJ6tpnSp7GeAO+gSctOY28xM76%0AHLrFLOa92x/oh8jVfk9AqDYrxFW4fB6sV1Rd1/hRjH0KZZZVxqWx2O12Y0Oz9Vo7bG6y5EafMR4z%0AMlCC6LlPUWdeQkVVNXjnGfpWvdrEmPE6Ho+j0THpA7tH7Xradu6qK9R7ueRBuZPnu6Q1lPsc2477%0AF/fpNpGXL3bcXF9zOOzwAk+efMowRL72o1/leDzy9LPjCEg7J6MA+JuOd9rAwHRzl4ClndDRwIin%0AHXpu9gcOh56+DwzRkURUWyVk9u0duhzltuZEN1COTW4x4RKJgZSg644cj0LXb6i8rpD7/c3YSdEM%0AmmIvknPH8zqTJei7HMvXxu9mIzNhM/N05ykvZvRwTvxeSmki0aV08jPj4zeM1WeGzbxDyd4m2ga2%0A6wPt0KsAlXi8r8dM0TITZJtfnptT57IEcg2LMY6JeVWnaohm58yMjZvaxNpnyy4Cpsqv+xvx3kL4%0ASZkQHKUU6nJoanoucPVFDPp4LpKw2WzYoCUQV1c3rFarXKDa0/dxlHRYr9ezjFjJmXqT8U4bGFuR%0AzLi0bTsyeo2I1Pc9bUhcvdrzre98wtALzq9pDweS1FlOM+CbWvmmeQLN/lJShqyBpM7N+CciZNAW%0AEgMxJbr+yLEd6Ic169WW73znW1xfX/PlLz1EBDarDV5MNcwyMdo2pc4s3zL9Doyr/Rg6ZeA2xkgK%0A2Q0ueCc5FTPelCXRrmSRngqhAlNNURIhxfyc0mM54cG8wRiGYfSubu+D0A49h2PHy92OIcJ6s8bX%0AFWIeXDbSVeUnAyoT2Lw0BmXIUvb7MaxOM4zXVKEfSwfM4BjhbpzYZPzPzxm2JsmZhkl3KMbIfr/H%0AspplN88yjPm8sFcN3XQs1r/odaM8r9vtlq4bGIaAz55ZipGbmysuthsOruVwvOHi4gK3T6zX6xEc%0Avrq6euPrC/8/MjC2YizxkhAC+13H9e7Aq5c3hFgxhJo+6ISOUfkTX1TtYgKV54JVIqIeTCZgIblc%0A32lIc319zTB0KiTdd4rVnJiU081zm2+RuK31ooYkqepdmlLHEidP45aXcWKb9v+y8HD8jUWCKIpm%0Ao34jmIzuPzMDAIyEuq4PtH3H/gi+Bld5pKrRFf92+1z7vZlRvuO47btGozf2q+ETKSlnCibV/vJ3%0A7Psx2L6rCH3fD/T9gKfUImLmbZVN8sw7mmU/X3O+YLrvvfczlb/yc+U5sHN0PB7RNrBqNFZVzeXl%0AOV/5kS/z+JNv8OLFK+5dPuD65SuiRFarWlP9klQK5S3GO29gTFfVWjaYWzrqZaTE1b7ls+evuNod%0AaeoLhuARt1JeRa1qK0PuZO+T3PJgSo0VuwmhaIqeUl5F1ftAlM15bCPH45797prd7povfelLtO2x%0A4F9ohshXWjwJc31WmAyaAXrl+170eykl+pEerulmTUfoARinpcRcYF5tvgQddXX2xGEYa3UAotOo%0AQBLEUPByMkYVT/TsiTl7VJ6vlPLzYt5PHTk9bTdwc9hz7HqqM/B1TZ9USrSu6lEYW49l8k5s0o7d%0AAwoC3fLc6nWrRrmF7XbL/fv3Z1iV4SLW5XB537ladXjW2+14fCVwbdtqmvVoFJpmPZazlMQ+M0jO%0AGcaTjVQovc7SEPckP+9wuTTW5cI79FG1Z4Cv/MiPcO/yAVdXey4u7nHv3gO++92P+LVvfZf9fs+D%0A+w9VByj/rfwPIdEOpglhvWfKSWSErK7TFiQkn6ukXc4qaXiSROt4VD3u9b7MiBdkoSbjwqfsPQzD%0AgPMqzbBZKyfi6ZMnAMUKJiM4vNzeqexH+V75mXGM3QcYPRdhfsOV+37qcfk/FM6Kk1wWwbyH0ReE%0AWpYZnOXKKnL7uFKWZohJNO1dOc3ZCWN6u6yUnnl8ErPRmMIgMzQzDkxhBI14ZwV+QwoaJhTYg4VK%0AZiTMAGkKWe8n67lVecYaNcVVhMZPpL2ynUjppY7GIf8/DEM2arfF5NUYMTt/pzzVcmGpvKdyNUMM%0AtMcjQz/w6NEj+m7gxXrNo0ePOOxbXr58SR8GwhA0EeEbjt3/ByCviPwh4I8C/3lK6d/Nr62APw78%0Ay8AG+CvAv5lS+rj43teAPwn848AB+LPAH0za9/qNhmUfuq4bJS+tuvrq6kpV6o5BlevqDTE5+iBE%0A6rEyJgKSiXVVvul1R6c0dQE55IvmSMkjUiOS06wxsTnbAgP3Hqx5cG9L03iePv0+6/Ua5zOe4zwy%0ArrqWblSzsMwc2UpvWaR8/rCskclcpaSeS0wRswMxRm1Qb0ZxkUUqX5uwl5hT5LPrPBqXseL5jsio%0A/O3y+yYEPu2/vbcIM0Vojy379qjuf1XhxSl3hhoRZeuWk9SySMpcjvk9N5uMNlnt3Jo3UmaPUko8%0AffoUv1nx4MGDnF4eCu8ijqzYUSCs8KRKwNm8VCBvbz2yb+ssR+nd1MxtNPj5POn9rEWQ59tLZaT3%0APdYXK9+JqipYnudiGMZmQHMMkeOhgyxFsttd853vfIdnTz+j9g3vv/8IgPWm4dXVnpubG9brNefn%0A5zx+/Ji3GW9tYESb3v/raHfHcvxnwO9D28p+hraP/XMi8pMppSDK6/7zwFPgHwMeAn8aXXT/7Tfc%0Ah1uvWexsVaR6oQLHPp/YqKnDlLkxOiYymNxpYNLoqeiHpxVL8Rat2Lb9ahrtPTwMqlWzWmuldyJg%0Ap71Mm5oHdSpEWv5/yrtxSTEaBXqzlxDmxsPOz/Lx7PkIjoIhxq+rLTp1/pduenm9SmOihohb+2Oh%0ArlSeWolFeKfYS+mtjIa2TEMvmpiZEYU5G3hKCfuR52GhxFJ/tjTKpeFXwznfnh1z+Rvj+WTuwZVF%0Ai+U5MtoETDpHZlRsP/V3mJ3nU+e73HeyiL0IVNlAdscDh+Oez559wuHQIr5GBIZOZSYcouUub8I/%0AKMZbGRgROQf+DPD7gT9SvH4P+FngX0kp/eX82s+gbWT/SeAvAP802rf6R1NKn+TP/PvAfy0ifzil%0A9IXh6uPxSIoD+/1+bFnS9z2vXr3ieDyqq9f3fPqk5Xjo6fsNcagZBq+N1QpA83Uu/yngTeUfLNXs%0AcRIyLUGFhgAO+5ZvfftX2e/3PHrvvhKYWq1ZicOAqxu0vazgyOQxmRuRcmVfYjDLG0qNYBrlDygm%0A++cZmvG1InM0c2O402m5tQ+nQq75udPJYXVGt3g4URXsVusaqWt8Al+vNCSIST0YqTBWwSxd7dLJ%0Ac6PGfsKibD9AJQ2eP39OXasY9oOHD7OkwiTuZOGReTVd11FVFauzzexY7f3SwKgXMVVEl8RAS0SU%0A19mwn7qu2e/3fPbZZzSNtlLRtLbtu4N66nu0DLdKAmNKidB2iK8zTqmY0o/92I/xwQdf5te+9ev8%0A8i//LT795NOMSW1H3MnIg28z3taD+ZPAn08p/WUR+SPF6z8J1Ex9p0kpfSIifwP43aiB+V3A3zDj%0AksdfAFb5+//zcmM57CrFJC8A4r6lO/akLiIdEBrSAO3Bsz84Xr1K7I891wdIaUWkJopWiCbCCOoC%0AuCSAJ7jiAqaU6eVC12fafaroGehiYEXSVGEKuCBIFKrk8QlqWTFE4f9t78xibdvSuv77xphzrrV2%0Ad7p7bt2+GiygoJAiBYIGqlRSINEY0AfqkeiDkZAYTASJD+KDEh9AtBAeDFFThgeeVDDEEoxGpSRa%0AoSuwOii4/bnnnmY3a6+15hyND98Yc441z9qnuVXnnrOp9Z3ss7qx5prjm3N84//1L73yOnvGY1cL%0AJDh2a4vBYypLZSJVqn6GRGxKbMnwe+xhoFg4IQRMUJBhrVGVKAZCyJnf9D2co9FgL5/C9EOItN7h%0AglevkVEjZiRqIe0QCMmYGKJmekdJlSnCYItx3ClMNOdHkDIPRgxOXApYBNDCU1orR7s4OudTw6/A%0AiXjMrGZvb48YoXIq4G1dkxMgjUBVZWNoRCRgxCOI5oRFGfKPxOAXq94uEmOgCxqpKgnB1Duzvl3s%0A7mwH16aM5cLbU1UVEnV3b5craCKrTnnQWK1b4zvfI46mqZjP532HRxGPtaHPJ2rTb+g11b8Q9Ld8%0A5zERZs2E09NTTpanGEKPuJTnTsMuoiZ15tY6WaBUItjKEuoK5xy3w5zV4kjVwskuzcRy+co+N2/e%0AxNqOZ5+5wu1bbzCf38JPV8x2Z0ym4MMpkeUdQuB+6IEFjIh8FBUE37zh46eANsZ4a/T+tfRZHnOt%0A/DDGeEtE2mLMmH4M+IfjN72PeNcyn5/S+cjJyZLFasm16ze4ffs2r1+7rqHf1T7WTKjspPdcDJtr%0AEZoum6V03l3KxVRGEUPOSzGpDITj859/DedbDg8P2T1Yj9YV0bICw24va5+Vu+8mNXB8bhuNtPeJ%0AXsZjy/eGz4ZcJFI7102/ne1F42PpgLFbGjCSOhqse7OsHUpZxKh1c1SdUTVpUAsG+8hYZRojvTIh%0ANoSArZMdJ0XQHhwcsLOzw4ULF/TzAoFkpGGM4eTkpDcKt22LSxHDAw88s9ksqequV2dKRDpOyi3v%0Ar/Ix1/GdzWZ9XNf42lSjKOPyninVNmMM+/v7hHBM2+p96VzgzTdv0rWeCxcu4F3k8uWL7O7u8pu/%0A+3uEEHju2Re4evUqk+nbUJNXRJ4H/jnwXTHGBxFpoyiKjWh7PKaknwB+qni9D7wMuqM6px4HzZJu%0AWa06VquOttWoWu0SoJmrb02TLE483RCt1zYpzqXqZQDRQdcRoyN4r2Uwq8EIfC9hsW78vPf4swQC%0AIwFwloA5S4W5c75l2kHsi2kPmti6mzs/rkW2huK3Q9FapFSNYuyzrEsbQ07wkxRblCNf+3qxI/vU%0AJr7GIrcrCj162dnZ6ZuuZWNwXa/X4i2FwXK57N3aXddBZdbUMpGcOT0IzXFMUz7m+Lrl97IqVwrL%0ATakOIoIUqSbja1DOPyPyPA/nW7pOy0yslpp/1blVUq0czz//PLdu3eL4+Fizrt+mZMcPAk8Cnyom%0AYYEPicgPAd8NNCJyaYRingR+PT1/HfjW8qAicglVrdaQTaYY4wpYFeMBWC5WINC6QNd5bh+ecPv2%0AEYe355yeOhanGuXoapVe3kWMuYsuGU3xItkg+p3b9AW+gwcvQx0VokL06B2umwMeW4NbrLBmKG40%0AGN3U0FZWvR9u0EFPL/OUzjzlDQim1MHV3Xt/wmYscIbjxD5jOaqte4RGhr+zGnSZSI9WYhBc0LgM%0AHwOdC3QhalveqP2qMuIIIfTellKgZHf/JiGb0UbJhxiDNrw3QiXCZDZTQTGdUDWqcvgYaF1HFSf9%0A93Nxp4wm8rXM7UuiKVGb2izExN5e1uenFd6mfMz8vU2G/PL9LKhy5cbyL8gQaNrfuSNEk6/JtKnY%0A3/c4N0PkmBiWqjrdvs21a28AQ/lQd/02Vy9fYTKZYYzh+PDwnvfiJnpQAfNrwDeM3vvXwGeAf4oa%0AczvgI8AvAojI08D7gR9J4z8J/AMReTrGmH1f34UKkE89yMksVitMqm+xWK64efM2N28ccTI/JUYB%0Ak7012rA+JxGqo2G8e98NQK1TjOrpaJ1j5TpM8BrBG7XMgLGR4DSnY39nF2NWawIGUra0KW+szbvP%0Avc5j0/PyvayC3a9QGR8vCxIx5U2foXw485h3CrJshDb993wMg21IJ6+LWIadOtsVdEGCyGDQDanr%0A4ljAnjXHsSE0x0o5p/YoCUNkeB5fRt1mo2eMsU+QzNfL+w6wGrMTApWtesFSIlNNZiXxELLtJTEg%0A/W5OHynHwcb7U0JS7YuNKkWU911BjcbWiKVXt0A9c88++zR1XXP79iHz+aJ3kHjvOTk5IQRNMdjd%0A3UMdvw9GDyRgYozHwKfX5icyB27EGD+dXv888JMicgO4icbE/C7wq+krnwB+H/i4iPw94HIa86/i%0AA3iQAI6Plqy6JUjF7VvH/N6nP8d8sWI6O2Bnf4/dncvqWWKCwmotZhRi2Q7UFAt8s5Apb7h8oy38%0AimZSce3agvZ0wV5T0VSW6BdMJhU7e5baCE1TMZ0MvZp0ka7f7MAdN76Pw5jejiDmjnHDdWDt/bXF%0AdYbQktHul3fsMRlj1jKps6epVB3y8fJ7GeaX+VQxFe3KnqOuc0OFf1E0IKJVAvMimE6HJMQ0Q2L0%0AeD/0bhrPu2matfMBRZGx3PmJxOCJyyWddwS08ptNdXNL5AJDr6HlUnf9ySR1n7B6DxljWLULgleE%0AQ0K3VW3WYrUADg4Oer6ZDSpOvsdKJFtep/KeWK1WvQu7DARcR8yK6FrnqOoKomZ+N03D4eExIsJk%0AokGhTz/zjlSa83UODw+5ffMWlbE0j1HJzB9GM7B+kSHQ7gdiTA0xNRbmLwM/C/wvikC7B/2h49MT%0A2uWKEC23D+fMFysWi47IClvPMLammViWnfoWhqzVTaSV6yALnnJRZn05P5f+JlZ9WgOjulVgf7fC%0AijZgi8FTmQllQtomQ25JZ72vgmJ4Xhqd83v3QiObnt8PmjnrPO7226Xw0edlEW9Vk5LjNkchgbGq%0AfoW8aAdvWkYRkZyguW63yL95pu3KDJEcMel5MWq2dhUDzXRKYDDojudQ2pNKFUTywpfBJey9Yzqd%0AgYQ++RYgxJQwmerciDHD8+K8jaHv4dUXGzPZM5HCEGIO4NMESP2e/n7brkYq5ZBS0Qt+owJyNpuw%0Av7/Lzs4OJyfzdBzDlStXaJqGo6MTmqbh9PT0nvfGJvqSBUyM8c+PXi/RgLkzg+ZijC8Cf+VL/e2X%0AXnyVxWJJ5+DkZM7i1DFfrLh91LFz3PHkO55lNtulit3I+FggCVPC60HIbIL+5aI2FpbtAusjtTFE%0A3xFcy6SasbczYbG6zWzSYML6DSSENQQzXhDjxTH+7fF55d0J7i5g7ieb+m6xDptVrDtVs3KnLXfQ%0A3LEghIDz2dBpwaB1bKL0iXtW6oR+hFy+oBQuIeSkVtvzpjSCjtMCoIg5SfV2fOuHDpTGMEmqg4j0%0AJTQz+iqTaDMqyyitrnPaR8qtyg3aLAmJaTH5xUJNiDnloC88NrKfAH2OUpnbVFVVj6LyHHM5ztzq%0ANZe7PD09XROIOZLX9dcZ6koFfdM0PPnkkxwfLXj55ZdZLOZqW+yEaTNhdnWHpmn69jsPSuc6F+n6%0A9esslyt8sNo0zeeq657FssU5ja61WaCQLKsbaJMeP35djukgwPYAACAASURBVHGJ4RKgdY6pVXfi%0ApUuXIHYsTgOxUrVsXcAU6QEj4TLeIe/47TMQTEw7290EzCaBeRYP7kb3QjCbjt2/F4boXR+juqlJ%0AnQCixhGVCzjXqO17E43C4kXW3f9lwNlYyERhKD8RY98iRUbfyR6mjJrKYLVNc1ovqRH7853P5xhj%0AaJp6rSngMLd1fo9V1RjX24/kcyxz7bz3BDP0ACsFjyKZdm1jySpiRjrZ/mRMxc7utE+B6LqO09MV%0AIQQmk9lawa0HpXMtYN64fiO1qWiYL1aslqkgt1SsVp6j4xPE1FQ7+0n3z3ET+v01pqWiTHHN6KYB%0Aagrr846cnNISCV7tCbWFZ596mieuXOLibs3LL/4hMXqsWGbNhCjLuwqYuxl574pguBPBbLoRxgil%0APOYYPZ0lY+4XwYwFzDB2sL/0zd2MNq+LxmopCpd6NPUVRAfbg6YBxGQ41UqClZ3088q7/NjblM8B%0ARr2HqhTEmBb9/oUD9i8cMJvN+nHZCCwiqdVMcweS2N3d1czqTrPZfejwqw7faTcJY/aIMVLXWlBb%0ABYwnRoP3Q73ckm/6e63eQ2l827qEeqSPr2nbFqmbJESExYIUEJg9YD6hq1TnyFhyoGKuqRPxfYb2%0AwcEBzzzzDEdHR/jVIfP5XDtdhsDp/BGpSI+SVqsVTd0QonYJsNaCMZigKOb0dElVzTnYPaDvQ8Nm%0AO8d4UZy1a+VHYwyu61T6z6ZcvXqVJ69e4ejGa3Rdx97eHnWj+vFZdoEz7QUbaBOCWT+vuwuYTc83%0Anc9bpTHPxgLxbuekgnd4HnzQTpq9AE5eJE1LSgI1rKGB/jiF6jme25qKm3kpuYRC0wuQrL6UqKDk%0AbTnHLMy6wjWuyKUhxqFLZomKsoAaC5XBBnOnHag0+jZN0x935QeEVSIloEdAJcJxTs+prmRol5JS%0AHwCm0wmr1WQjin4rdK4FjFsE/KrD1kJtakRa8B5jhSrCqj3h+MQxvbLP7s4+IUHw5bKlqTLsS7Az%0AGb8qDFFC0d9Hb/C6qvCdY2IqKiM0C2GnOuB973kvT7/jKZ5/6kkqgU9+9jO41mMnERGPqSOzGLGF%0AoDF26EIY8ZBiKaw11BhEtJxnbo8SomhovUgqV6ARrpHQx9SUwrNHXNQQPU1IHqI43NQehdbaESHl%0ABkWtkpYzbwEi2W0rCJYQfYqDgRA7Yv4nUZtFiiaTZhWkc9nOM6ELMG87ghcCVo+Z0FcIGt4vCA2O%0A6GPfIjfGSCUWK3YI2S8Ehs/pHhgkCnUc8rZAXexeUlfI3K9MNP2hrivqpuHC7owLuzNit8LR0bUR%0Aa7SmjIsdzaQiiKY22LrCp+u5XGpOkqkmROeJWKypaV2gqmpEbBI6JCRBX67DGBJSiWspAHqfCt6H%0AHsWA0ch1n1ENxCjM6kHYqHDWVIa8oQrC1O6AhWXbgo94L6zcEiOWizuXOF21PPf0jOVyyXLZUVUT%0AKrPL7du3OT4+pus8092Jpi4/IJ1rAdN6hzhPTdU3YBeRoUtggrir1YrpdMqkUUNeu+zOlNBl+nss%0AEEOv93YOKw0GuLR/wHPPPMvFCwc0tkJwfXHkyggEreQ+UFqoa+oR5AA/kcEVLTKUYpAH2ERKuL1J%0AVRmPGfOg/GyM4u5uZ8lPFF1ktSjzLhczz6oVSRBJ4kkI6h3JRtWeH2ao3raprkset2mn3aQm5fe1%0AdzVMJhMmKYgun9/JiXpOTJMS/bxL51zYfSSrMopGLNK3E8koxhQCXQGJwZgq2T3yRpBVcv0MUo5W%0AiEOL375nFn3gpIhmOdsqlw2R/p7X+Wqt35IHmZ9ZvTJi2dk5YOU8Xae5Wbu7u6oathoZnxOGJ02Z%0ACnj/dL4FzKojIri4VIlNuiGd19orIbBaLLn55g0MwoXnDgCDNYbT+XLNPqD1RgSXg7f6/1IYSYhU%0AUWiM5dLuPh9851dx8eJFXnjqaZrKcOvGaxwf3mQ1P2Q6s+pZIiYGa4sTKaI6TSol0u80ab30iygW%0ACyf3lD6DD+WCLyFxfj3O9Slfl8bFEAMxZE/NUFQ6xhTGn/T3bPvR3x6Ei8YY5Qxpvcm9046Fzre0%0AyQgfUIO7qXRhBLSnkxZo15nWdY1t6r5txibvkHNOi3xlg206Z0OFEdHgwMyDXJVPhkhgilavt27d%0A6jeiZlJx5coVrNFsZjEJxUWdk9q/6M9BWwdnR0IySgeDr6Btte+3C57JZIaI5ejo9trCzz2rs0CW%0AOBhxs2pVGpV3U/U8VZuHeyrHF00rrW2T1aFQ9E6aTqc0DbhwQte6Prfq5OSEa9eu8eLLr6iR90Q9%0AT5cvX+b0dMly9TYlOz5OFEXrN4YQ+wpuecFahGAE7ztc27E8XeDaDmsts9lMXXeewlWbjpnjSssN%0AMWgzdIlQRcvOZIeveuE97O/sMqsbYnB0yyXz+SHWROoKaiN40dbmkdCXFtBcGvVu5SArhbL63KLq%0AUL/raMjDmnDpUVGBsEoau5vPQh5noZpNCCYm2JGNy+u/a8i5RRprlOJcwiDMOi+96iQi+ChICGAM%0ALo1xSZBOUqmCrCKN+z1nuptNreSFCq51pqkwUATiw9BBIIQwBPbFFGBnzdr3Qgi9ilQb7WPebwQJ%0AAZvMt2zULm6obO8A1jo+9tfFdYMhXNbTDKqqoipr+qY0BxW+KcgvISfvXVKz0gZlBj5OJhOIguvo%0AO52Czvf4+JjlqWc+nzOdTqnrCVevXuXzL71xJp/PonMtYIxUZOOm3uAVYgr1IwoOaLsVJ/PjPnFr%0Af79mZzrDR63wpUV93NrOlEkA7xw2qPqyN53x5MXLXNq5wM7ulK5b0i5PWS6OWS5OqBvBVoI1Gvgk%0AMeIlN2kTtJfS+sLoH7FrO9sm5GLGJ1jQJm/EJuGySdCMj9G/Xzra7vj+EGsxeOEG1SijmxjXuxqo%0Ap0+LZJN2YVUR9JybRksdaBxMGbekxuw8L81F6psn5LOkL1eRu0t6lyJugVKIJhXaJPUrC5acKU3M%0AruukGhnpawiXCBHQMhdRBYyEiLM5dy27gwPdymGlYrVo++tcmZrT1PTN76gAiWFZ1CcecpYUlWir%0Am4x0mzRray1SqR0qRC1FQkJU2YRukgdMRI3aMUDw6iXLNa0nkwnT6ZTF/KSvsbS/f4Hd1CvqQelc%0AC5iUUaHFkcQQfcR1jiqhg67z1EZrayyP5/zB5z/H3t4eL7zr3VomsZkwmWi9jeMjp2pSLDwxQRAX%0AaKRiYg37zS7f8nUf4PlnnuXJgyc4Oj7k+OhNDo+uszi9yauv/AF7F2smU6hM7D0GdlalxZMrLGZ1%0AZVzGQXdRw2DAFIod2qvxuUc4Zl1A6Zy7NQSjBls/7LzpxnXe3aFaRYbG7BmthGwwSVQKr1QhphBs%0A9DBdpMJa8H6lrTK8Xicfk5s+RaEaY6imM405SShOUmBkLqkQ0fG5kJaghlsjKe8nBeblnb5fkMQ+%0A/qVUOTMvsj3M9s3nPRcvXqRpGlarFUZSZ07RfDYXPD7H5ERFJqZqIDVWA5hNalarFZNGW4JEP+Q6%0AXbv2GtPplBBUNZnNZlSV4bOf/QzOub5kxBMXdpKgbTBVavdaFLH3qyWTyYSdnR2OO+1UERlq/OZr%0A4L02um8aTQNwMaNAQxT1Rl17/QYuwpUrV9jZ2aF1nslkwmLuuHjxYrJN8egieR8lCVZ7R/fN0rNK%0AEfsdTyRiYgAP3arllDnXXnuNi5cva73RgwsqZOpFCqNOCZEYxbdO817qaofLBxd46uITXJzu4dsO%0A8brYrTUcHt5i5Rbsm1y2MXcn0L5LEVXfksuH3ugynlOxnvOIGHWBREnzyx6u0W56Fo0NnGPDXy8g%0A7pHs2QskySqGqqgx5GS7bEsyeJ/SI6JJm8BgXDXGasGtpkZsTT1pEGxvS4l+QKXZk7aeAFjwS4A+%0AITCX4lxvXxNjYJCbRdfDwr27Wq2YzWZr7umSstDOLuRsGymN0jYLeopeT0nVCc6zcl7LUBpDbStc%0A2+Ebx2wyZcWK+fEJ3aplf2oSkmowJnuThgjmGG1SfxwRg++cRkr7gLV1shcZrWWc7hlCxNg8d0vn%0AdbOp6xpCJIRV39NpuVz2Na41qdNqMbS3QOdawAQxfWBW750gqSZo3dHKWoJLO5YBt2p56aUXuX79%0AOs10yjvf/S729g44ODjAOcfy9FCRD5IqzAmTquYb3/u1fOBr38/7XngP0UXaeac71+kcIfDHr3yB%0AahKoJgFTey2RkESE9y1a1aKiqiylW3kgzZXqb+5CHZGgCYEGTc/vXZJFBTNYP+bYoFtSXughhL6C%0AvaKVs1MFdMGUqCa/n1ShoOfuUvChd6pCeR81otpaTFUxbSbYWg23djJN8S01LgbCYkHnXe+9Sw5x%0AVYeQXuIak4SDToacYxbTnxuVoMQapKhH09tlQoq7SWN3d3f71r51XWuHgKpKPc21Lo0Q+gTDqqqI%0AnaddLgneY+s6bTiW6D0+oQiJEUQ7XCyWx33AHYAYz9PPXKVtW65fv85qteAPv/C5PoR/Z2enj3vp%0AA/yiJ/pOH+sJIWi/7rqeUNcqZMREmlRcPHvxYsyqVUXrVKA0TQN+sPXkQMNnn61ZLDS7+ujohJs3%0Ab555b9yNzrWAiamOrUYrroOCDJlFhEmtMR8+BrwJ2GBYLE5ZdZ1e1K7liStPahtNs0e7WOIWHcRI%0AjWGnmfCup57l6StXsV6IzhPEEr0G+63inCiBye6EaFMZhmSzKVGByCAIdAcNrNegSWsoTSYLF/Us%0ADG7zbHIsbSJnGTrvhW4ehO5EOuvqkdoIcjuQocSBcw6pG6ytqJo69ZButFumWO0imXKUgh+S9sYC%0AM/NuTKURtBxT5nrZZIPJBcyzxyqjkPyoQWi2FzB9vFIEjOBdt8YLUwisjH6qqurzqoyeEFVlMKbG%0AGG0rnPswQcAYqGvLlSuXWC6X3HrtlOA8J0fH+M4xm83WUKdPjgAnBrJhl/VgQhWkq7X7y8dcPGtA%0Ar845XNHLKgcDZpvMhQsXaJop09nbUNHucSP1GKEJc2EIGZegrlFN0LU0lSE2lpP5At+5vgCT8x2v%0Avvoqb7x5XS3mOzs8fXGf3Z0dgjjwkd1pw7NXnuJr3/On2K+nxEVLIzXUltNTx6preeXaS+xe2MFU%0Anmi9BsmJIiBTVZgmp88PQmYd7t+Zsg/0u65Ju7eIYNdUnM2V+/NxyjB7AB+GRM6sz5cL14jBnwFi%0ASgTTe5EC5KC+ELKKJHgXtYxG6uIgYntXbNM0VLbRUH1TEWJMRnYKG4oeU+1WGZf0kU5kt/4aSmFY%0A9LnnlPQuXEtjtTujL4ViiivJiYUxap2XZrKrQtDkpEsNbOySLSQLnRACldGSm75zRK/Fun1CGpUY%0AfDqu75bJ9W6JvlUbnQRWixNCCCyXKnQuHuxyaeddffwWBNpO7TvZ44QPmvgZncbCJONeuzzFt7W2%0AyDFVejTk8IJTr+UdYmzJ1ZEPDg7oQkRQe9OyVTWpXUZu3brFYrGgbbuiVcqD0fkWMPkxxzykxRTD%0Aeuan9546VUUTEawxeKd6dEg31eHhIcu2Zc/Cwe6BXpwQ2Tc7PPHEExzsHWBbTyXa86aNufGVsFwu%0AsY2l606BGVECRqpezxezHvD0wPMs7CVv5RibvEmbPE73OnJpgznrc2tqvLSprswQJHdWgNyah6z3%0AmNw53yxMxvakcn5r9qRibuPf648pQ5LhOF5o09zy51lwgSZq5sjiPIcu2aRKG1qus1OmDLRt2/9W%0A7kZa1zWzqtZNJYxQW4rzKQPwQhiKq3ddhyP0RcZzyoP3KWctxcd4H7QgfO/dW28KV1VVb1darVbM%0A5wuWi6/AOBjB9J4E5z0iqvNHBKyiCJ8CsYJ3NI3q16fLFbWACdpQzPvA/MZtFuaIbjnn0oU5T114%0AgkvTPb7+mRf4xhe+ht2jluAi0kw4cS2xniLW8Mabf8zp8k329x1TqYmdIKHCGrVx1DaAa/rFVUmV%0Asrq12j6AjeraJAZIejNANBrPk0lVLqUYI4SR0VhyQJhF44ADRiJB/BABmpq+BZ8KeUsK6pJUB7aq%0A01j9Je9L9KKIRSKprm6rqQsxYry6pzsfiC7ig+Cih7rBNhY3AdOAbQxBVC0QIj74hH7Amows6iRc%0ASkRTLnqLiDYPAwbUJQFjIdAhEhQ9pq4NXVEgPPNvcHV7YnCQHjXSNl2bZCvxzkHntYVKEdbfuVPE%0AOEwdqGrLYqnu3SrVsqmT6uWyUAge5zrth26lR0RSR04XJ/jjDrNzQadj172MZY9stV1ZVn5OuzhN%0AIQ76Z8RibU3rSLaiZItpHdbW2MrQOlWZlqul1t8RFVi1NQRbpcLlkr57g3C2ee6udK4FDNynB0VE%0AjcHoharreq1ymzGGzmn+S3dboe40VkwODJOdGWJzPIQjh20611JVhvl83teGzW7X/LvZcBZltBOx%0Avvvmx/Fund2hD8qLs1DOGAGsqTtx8+P6sWXteYxx7fw2oSKTdkVTDaH+4/Hl/LP7+Cy6HxQ39pTd%0AjbLdpKwAB6mQWDGutFHkeZRop7x2zjlSD77eKJ8/02NHRBx5+VlraeppX17Bu3z9i+ZtIfbv5yBA%0A7yI0qJ1F1u+ljJoUoSTk1DQ4pw0IfUpdCEGDIi2miChWI/dkoihmMpmkwlYPTudawIQQ+naqJY0X%0AyVpnQtFCOqorp5oZIjS1hiy1vmVxMuelk5dY7h0z/+pvIhpBrGCilnUkBqpaWHUti+UJ090GZIm1%0AjapDDFm9Od3eiKItW9SbNTK0hBWkb2WySRBtmt/9GnrPShfInqMsaFRgmDVVIAer6XeK1IKYBRTJ%0AzRm1aJT3PeTOEaO2rqhmqkbkCFUAa6t+AZQCoRRCYwF8d96sfz/basaCdczLfJ65P/UQ2BbITerz%0AYrW27oVSXpx9h89o8GlMRtO+bZMAmfRCSaRLaEPQmvHSt4h1LnnRBIwthF7U6nsxRsS7/t7KRnG1%0ARyp6qetJL2BK+1Zsu7RZVsQgvbE4e6iCU1vQfD7n6PCQ09NT2rZlfnyCax+4qzNwzgXM3Whtpy49%0AOemzaTPB2aHwcxZCkuq/tF3LPLlNA17DwQUN6jORqhaOT25hrWbFmgSFiYKxBkNFrnRWLozx8/F7%0A/aKFPuy7X0ijuJdSxx/bWTblHpVCpdx91wXM5ojf0lM05nEkpmJOKcALVe/yIigNhJtQSykEYhxs%0AF5sM2KWnJLeJLUYo3wpBfT8mq/I8y1owkoMNC16W/MzlJ0vK4fwS6YPjRARbFx0dxWJNlfjiksA1%0AQ/a4z3V5soF73QaUhWJVxZQBnxoAYlK8kQO0up7yUGNZooD1FWI9xIoYU6qEz73Wo+qbyVidbWd1%0AY78yvUi6kd7bRSsFklEmOuZdR13rrgU5zsGy7BbUaaderVas3Iql6+ii0wQ68SBqwf/jFz/HZGoI%0AOJpGe+GoN7NKMTQaf2BFLSKSdgyTBUsSHv1nWe24B4K521zHi0CNen6I/YiREAcUUapIpYC5Q5Ua%0AC5g4dAOQ4vMsaEQ0/sTWupCWbtkH2Q3GRG1j6rqhEJbu8HeijQdRezJ6uh/KCynbWkrhIeneynVW%0AcuJgGRGtP5PtRdLH1uh5pqBNYxPCMIhoqL4xFZWtmTRTTubHeO9T3k/Tq9xrLWWNYTqdDR7B5P5X%0AQZhsc1EgISd1Zg+hAuAxVc1ieUrwkbqeUNUTpk1D6wJ0Xjt4EvDBcf3112nblul0Rm0su9OvwGxq%0AY4ZFeS8PAtDHlASG2qgiQl1VrFqFkzM7wYdAU9e0XceyXdH5lmY6IbQdQQJVZTic36BzS3zomM6s%0ABlRJxFRFLpQxVJZ1tWjkSYF1m4sxJgmywrib7To+rL8u1KJ7zb2MFYlpl9UFM5RGEBG6dnidPQzD%0AMQc7SQwhBeYlQ6v3uKALtms7QohMk1vaE6mrnBFdFVGwOZdpvRTmJsNTidDGgmYwfCZ0Q9mZcT02%0AJo8t2/LmFIsYVWUe7EXSe3oGO83wvaqqWK0Wa+fXJ2dm5FPkEamKpMfI5SljjMymO3pOVSooZSaE%0AENY8T/29kZ0FMVKHgKlNEkTDfbfWmyoW+WLBU9uKWCmKknTdamsIwRJDYHe2Q3BazuHo6IjpdErb%0Artjb37vjmtwPnWsBo27HO1tu3jEub7rpOybBVwn0pRMrk1LijRC7DkTwBL7wR1/kqctP8J4rT2Fz%0AQpE1/NZvf5Lrb77K7pUaqVa4Ppkx5YKkztDaioNeaCT1el1VAojrbs08vxKiZ7elT/O0fYGiAank%0A74+FzVmv++esI5bgi9otDJ6k0h7jCbrrxZgyoiGgu2427GINFjBNVpXM2u/CsIB69LVBQJbnVrzq%0A31uzs2wAOZsM3PnRe99HsHZdh+2qvl1JHjMI9XUVdDDEJnVGUvhClOTZ0cx57zoqK1S2wc5qKjvB%0Ah466bvpyFJraIlSV/nY9vdNonn8bUY+g9wGRuheu+VplviJBhcmaam5VjTeGduV1w8Vga8vFiwdM%0AJjXv//r3cXJywptv3sSIhma8FTrXAiZTKVzGF0OZmnYXtB+O2kpiv2hzoWfV/7VRe6brN67z0ksv%0AcvLer+NgZ5cInJ7MuXnrOm13yoVqik/9iY1ZdyNniH0voy3Fd8oxGTWU6gsM+/vY7jIWIkP28p2x%0AL3d8rw9AGyNBNp9LWsXaXyj0yHAw4A69ebTuSo4XsWvdDGDdqLsJffX83ID81vmWx53J4ju+k+cz%0AILYB8WxCir33jHXBM46fGZ+rMVVCGQaTWs1aoyEBeozMX1glg+q4S2ap6ma+SVR3dXZ2xBjJLVT6%0AMSmKIbqgNkQGVVjd7cLKuX4DGc5Jo45DCH2Q5oPSuRYw2VszRjBjNGNQd2EWMlG0TgtxcLVmlaZJ%0A8StBQKrIa29c4ze7wDe+6728+/nnmO3t8vKrL9G5OXWjZSNdaJnuVqmYUmm4HHs0NntE7rjp8/zu%0AgsrK8eUxx0IF7hQ0dxh4Y+FNSpB6MGAWXRYLg3NGgyEEQjLySorTMdYik2aouA9FRf2z7Si9UfRu%0ANSnK+RPv4F1GtXf9XkYBDPMpOzXWBTIseaePw3HG1zDP1RiDQfqguxgjla1wTvtrV5XFuUBdKz9I%0AJS5yLaPVqkv8lj7mpldNi3MHkFh0TuhTAVIyiRTR7aIdTTUGy6uqFjtVc6PBOVWzou+I3lNVmpf0%0AzDPP8PLLL/PKK6/e1zUZ07kWMJnuhWAE0ZyR0ecwJLoBEHNtXEuMAawhtIGTkxNefOVFJk3Fs9Wz%0AqcoZaocICm21snyHqYZOkb3N5Yybcgzbx1QiBRHpof9YMJW71Tg2424q0vi3No0dUIHyazh3NM3F%0Al+ckvbDuvTGpHkmJiO7c6WOvqnjv+6zk8TXezJ8NKtIZAmasIpXf6bpu/bxDIAZXqBsZTRQ2thEy%0AXfsrNr/y+Cp0qyTEVcioyjMIPFvrslSvZbbdCnXdUFKMEb8aSnGosCqSW0NYO8dKhsJggYCIoXNo%0AJruLKaq9ZbVaMJ/PWS6XxBR6sLMz28jTe9G5FjAu+N4jA+B7z4hSSGpFEA9S6vnJZoHrex9jdLc9%0AaY9VRwWIwmlcsVy2/Pof/DZvhFu8Z/kaR4e3uBVuaAKdn1JXNadzdTVa6fB0qW7qlNNFwJrQ33DW%0Aho2LpTfiFTdwRgCZxsJh4odiQpHBW1Tuut57uqhG1wytQwy0rRoQvct1YQwhRLq40pvfpxYisYWM%0AOsQO6lAIuJUjSk3XebxUirylYtm1XDw4wIWA7Rxd8DiZUlUZUQ2LLp9nCIHOaaCZuPU4mMEw3iug%0A6cNar2/auTVqF5xfNxzTVxEcVIB8XGt7zyx1M8X5yPx0yXLZYqRisdRataWRurweJlVVdClPqesc%0Ada2GbOc888WSSMS5jrqqmEynuDDYvCpryRqiGI28FZsLQw0bSU5HMEbr5tZ1TYgBYy3z+XzwEBbu%0Ac+9db6TXe9z0MUrWaCKud6q+BW+JQbh584jjoxNevf4qy8UK54RXX3mdrrs/VDkmudsO+riSiDwL%0AvPyoz2NLW/oKpOdijK/c7+DzKmAE+GrgM8BzwPGjPaNHTvuowN3yYsuLkr7cvNgHXo0PIDTOpYoU%0AY4wi8lp6eRxjPHqkJ/SIqVCjtrzY8qKnh8CLBz7G/YU7bmlLW9rSW6CtgNnSlrb00Og8C5gV8I/S%0A41c6bXkx0JYXAz1yXpxLI++WtrSl80HnGcFsaUtbesxpK2C2tKUtPTTaCpgtbWlLD422AmZLW9rS%0AQ6OtgNnSlrb00OhcChgR+UER+aKILEXkUyLyHY/6nL7cJCIfEpFfEpFXRSSKyPeOPhcR+fH0+UJE%0A/puIfP1ozCUR+biIHKa/j4vIxbd3Jl86iciPicj/EZFjEXlDRP69iHzNaMxERD4mIm+KyFxE/qOI%0APDca80Li6TyN+xcisp6i/JiTiPxtEfkdETlKf58Uke8pPn+s+HDuBIyIfD/w08A/Br4J+B/Ar4jI%0AC4/0xL78tAv8NvBDZ3z+I8DfTZ9/C/A68F9EZL8Y8wvAB4C/lP4+AHz8YZ3wQ6QPA/8S+DbgI2iK%0AyydEZLcY89PA9wEfBb4d2AN+WVLJufT4n1C+fnsa99eBn3yb5vDlopeBvw98c/r7r8B/KDaXx4sP%0AZ1U7e1z/gN8Afm703v8DfuJRn9tDnHMEvrd4LcBrwI8W702A28DfSq/fl773rcWYb0vvfc2jntOX%0AyI+raR4fSq8vAC3w/cWYZ9BqNd+dXn9Pev1MMeajwBI4eNRz+hL5cRP4m48jH84Vgkkw7oPAJ0Yf%0AfQL4c2//GT0yejfwFAUfYowr4L8z8OHPAocxxt8oxvxv4JDzz6sL6fFmevwgULPOj1eBT7POj0+n%0A9zP9Z1Qwf/Chnu1DIhGxIvJRFI18kseQD+ctm/oJwALXRu9fQxfcVwrluW7iwzuLMW9s+O4bnGNe%0ApVIdPwX8zxjjp9PbTwFtjPHWaHh5XzzFiF8xxlsiIOuxQAAAAmFJREFU0nLO+CEi34AKlClwAnxf%0AjPH3ReQDPGZ8OG8CJtM4v2Fzr4s/+XQvPmziyXnn1c8Afxq1H9yL/qTy47OoPe0iaj/5tyLy4buM%0Af2R8OFcqEvAmqj+OJe2T3Lmb/0mm19Pj3fjwOvCODd+9yjnllYh8DPirwF+IMZYVDV8HGhG5NPrK%0AmB9r/Erja84ZP2KMbYzxCzHG/xtj/DHUGfB3eAz5cK4ETIyxBT6FehJK+gjw62//GT0y+iJ6o/R8%0ASPapDzPw4ZPABRH5M8WYb0XtF+eKV8kl/zPAXwP+Yozxi6MhnwI61vnxNPB+1vnx/vR+pu9CM40/%0A9bDO/W0iQW0ojx8fHrUF/C1YzL8ftZT/DdRT8s9QPfSdj/rcvszz3ENh8AdQ6PrD6fkL6fMfRb1G%0A35duoF8AXgX2i2P8Crq7fVv6+x3glx713N4CL342zfXD6O6b/2bFmJ8DXgK+Ew1f+DXgtwCbPrfA%0A7wK/mj7/zjT+Y496fg/Ii38CfAfwLuAb0HAND3zkceTDI2fYW2TyDwJ/xCB1P/Soz+khzPHP07cL%0AXPv7N+lzAX4cdVcvUQ/S+0fHuAz8O7TU4VF6fvFRz+0t8GITHyLwA8WYKfAx4AZwCvwS8PzoOC8A%0Av5w+v5HGTx71/B6QFz9f3PtvJEHxkceVD9t6MFva0pYeGp0rG8yWtrSl80VbAbOlLW3podFWwGxp%0AS1t6aLQVMFva0pYeGm0FzJa2tKWHRlsBs6Utbemh0VbAbGlLW3potBUwW9rSlh4abQXMlra0pYdG%0AWwGzpS1t6aHRVsBsaUtbemj0/wFYt+D0T6biHwAAAABJRU5ErkJggg==" alt="" />
What to remember from this assignment:
- 预处理你的数据集很重要Preprocessing the dataset is important.
- 你分别实现每个函数: initialize(), propagate(), optimize(). 然后你整合成 一个 model().
- 调整你的learning rate (which is an example of a "hyperparameter") 可以对算法产生很大的影响.
代码综合
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset # 用来导入数据集的
import skimage
%matplotlib inline
# Loading the data (cat/non-cat)
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
### START CODE HERE ### (≈ 3 lines of code)
m_train = train_set_y.shape[1] # or train_set_x_orig.shape[0]
m_test = test_set_y.shape[1]
num_px = train_set_x_orig.shape[1]
### END CODE HERE ###
print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
# Reshape the training and test examples
### START CODE HERE ### (≈ 2 lines of code)
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
### END CODE HERE ###
print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
print ("sanity check after reshaping: " + str(train_set_x_flatten[0:5,0]))
train_set_x = train_set_x_flatten / 255.
test_set_x = test_set_x_flatten / 255.
# GRADED FUNCTION: sigmoid
def sigmoid(z):
"""
Compute the sigmoid of z
Arguments:
x -- A scalar or numpy array of any size.
Return:
s -- sigmoid(z)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1 / (1 + np.exp(-z))
### END CODE HERE ###
return s
# GRADED FUNCTION: initialize_with_zeros
def initialize_with_zeros(dim):
"""
This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
Argument:
dim -- size of the w vector we want (or number of parameters in this case)
Returns:
w -- initialized vector of shape (dim, 1)
b -- initialized scalar (corresponds to the bias)
"""
### START CODE HERE ### (≈ 1 line of code)
w = np.zeros(shape=(dim, 1))
b = 0
### END CODE HERE ###
assert(w.shape == (dim, 1)) # 判断 w 的shape是否为 (dim, 1), 不是则终止程序
assert(isinstance(b, float) or isinstance(b, int)) # 判断 b 是否是float或者int类型
return w, b
# GRADED FUNCTION: propagate
def propagate(w, b, X, Y):
"""
Implement the cost function and its gradient for the propagation explained above
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)
Return:
cost -- negative log-likelihood cost for logistic regression
dw -- gradient of the loss with respect to w, thus same shape as w
db -- gradient of the loss with respect to b, thus same shape as b
Tips:
- Write your code step by step for the propagation
"""
m = X.shape[1] # 样例数
# print(m)
# 前向传播(Forward Propagation) (FROM X TO COST)
### START CODE HERE ### (≈ 2 lines of code)
A = sigmoid(np.dot(w.T, X) + b) # 计算 activation , A 的 维度是 (m, m)
cost = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * (np.log(1 - A))) # 计算 cost; Y == yhat(1, m)
### END CODE HERE ###
# 反向传播(Backward Propagation) (TO FIND GRAD)
### START CODE HERE ### (≈ 2 lines of code)
dw = (1 / m) * np.dot(X, (A - Y).T) # 计算 w 的导数
db = (1 / m) * np.sum(A - Y) # 计算 b 的导数
### END CODE HERE ###
assert(dw.shape == w.shape) # 这些代码 会 减少bug出现
assert(db.dtype == float) # db 是一个值
cost = np.squeeze(cost) # 压缩维度,(从数组的形状中删除单维条目,即把shape中为1的维度去掉)
assert(cost.shape == ())
grads = {"dw": dw,
"db": db}
return grads, cost
# GRADED FUNCTION: optimize
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
"""
This function optimizes w and b by running a gradient descent algorithm
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat), of shape (1, number of examples)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- True to print the loss every 100 steps
Returns:
params -- dictionary containing the weights w and bias b
grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
Tips:
You basically need to write down two steps and iterate through them:
1) Calculate the cost and the gradient for the current parameters. Use propagate().
2) Update the parameters using gradient descent rule for w and b.
"""
costs = []
for i in range(num_iterations):
# Cost and gradient calculation
### START CODE HERE ###
grads, cost = propagate(w, b, X, Y)
### END CODE HERE ###
# Retrieve derivatives from grads(获取导数)
dw = grads["dw"]
db = grads["db"]
# update rule (更新 参数)
### START CODE HERE ###
w = w - learning_rate * dw # need to broadcast
b = b - learning_rate * db
### END CODE HERE ###
# Record the costs (每一百次记录一次 cost)
if i % 100 == 0:
costs.append(cost)
# Print the cost every 100 training examples (如果需要打印则每一百次打印一次)
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" % (i, cost))
# 记录 迭代好的参数 (w, b)
params = {"w": w,
"b": b}
# 记录当前导数(dw, db), 以便下次继续迭代
grads = {"dw": dw,
"db": db}
return params, grads, costs
# GRADED FUNCTION: predict
def predict(w, b, X):
'''
Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Returns:
Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
'''
m = X.shape[1]
Y_prediction = np.zeros((1, m))
w = w.reshape(X.shape[0], 1)
# Compute vector "A" predicting the probabilities of a cat being present in the picture
### START CODE HERE ### (≈ 1 line of code)
A = sigmoid(np.dot(w.T, X) + b)
### END CODE HERE ###
for i in range(A.shape[1]):
# Convert probabilities a[0,i] to actual predictions p[0,i]
### START CODE HERE ### (≈ 4 lines of code)
Y_prediction[0, i] = 1 if A[0, i] > 0.5 else 0
### END CODE HERE ###
assert(Y_prediction.shape == (1, m))
return Y_prediction
# GRADED FUNCTION: model
def model(X_train, Y_train, X_test, Y_test, num_iterations=2000, learning_rate=0.5, print_cost=False):
"""
Builds the logistic regression model by calling the function you've implemented previously
Arguments:
X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
print_cost -- Set to true to print the cost every 100 iterations
Returns:
d -- dictionary containing information about the model.
"""
### START CODE HERE ###
# initialize parameters with zeros (初始化参数(w, b))
w, b = initialize_with_zeros(X_train.shape[0]) # num_px*num_px*3
# Gradient descent (前向传播和后向传播 同时 梯度下降更新参数)
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
# Retrieve parameters w and b from dictionary "parameters"(获取参数w, b)
w = parameters["w"]
b = parameters["b"]
# Predict test/train set examples (使用测试集和训练集进行预测)
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
### END CODE HERE ###
# Print train/test Errors (训练/测试误差: (100 - mean(abs(Y_hat - Y))*100 )
print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
# Example of a picture that was wrongly classified.
index = 24
plt.imshow(test_set_x[:,index].reshape((num_px, num_px, 3)))
# test_set_y[0, index]:测试集里标签; classes[int(d["Y_Prediction_test"][0, index])]:预测值
print ("y = " + str(test_set_y[0, index]) + ", you predicted that it is a \"" +
classes[int(d["Y_prediction_test"][0, index])].decode("utf-8") + "\" picture.")
- 吴恩达《深度学习》-第一门课 (Neural Networks and Deep Learning)-第二周:(Basics of Neural Network programming)-课程笔记
第二周:神经网络的编程基础 (Basics of Neural Network programming) 2.1.二分类(Binary Classification) 二分类问题的目标就是习得一个分类 ...
- Coursera, Deep Learning 1, Neural Networks and Deep Learning - week2, Neural Networks Basics
Logistic regression Cost function for logistic regression Gradient Descent 接下来主要讲 Vectorization Logi ...
- 【DeepLearning学习笔记】Coursera课程《Neural Networks and Deep Learning》——Week2 Neural Networks Basics课堂笔记
Coursera课程<Neural Networks and Deep Learning> deeplearning.ai Week2 Neural Networks Basics 2.1 ...
- Neural Networks and Deep Learning
Neural Networks and Deep Learning This is the first course of the deep learning specialization at Co ...
- [C3] Andrew Ng - Neural Networks and Deep Learning
About this Course If you want to break into cutting-edge AI, this course will help you do so. Deep l ...
- Neural Networks and Deep Learning学习笔记ch1 - 神经网络
近期開始看一些深度学习的资料.想学习一下深度学习的基础知识.找到了一个比較好的tutorial,Neural Networks and Deep Learning,认真看完了之后觉得收获还是非常多的. ...
- 第四节,Neural Networks and Deep Learning 一书小节(上)
最近花了半个多月把Mchiael Nielsen所写的Neural Networks and Deep Learning这本书看了一遍,受益匪浅. 该书英文原版地址地址:http://neuralne ...
- 【DeepLearning学习笔记】Coursera课程《Neural Networks and Deep Learning》——Week1 Introduction to deep learning课堂笔记
Coursera课程<Neural Networks and Deep Learning> deeplearning.ai Week1 Introduction to deep learn ...
- 课程一(Neural Networks and Deep Learning),第二周(Basics of Neural Network programming)—— 4、Logistic Regression with a Neural Network mindset
Logistic Regression with a Neural Network mindset Welcome to the first (required) programming exerci ...
随机推荐
- JS平滑无缝滚动实现———实现首页广告自动滚动效果(附实例)
本文我们实现纯JS方式的滚动广告效果. 先show一下成品: 首先是网页样式: 1. #demo { 2. background: #FFF; 3. overflow:hidden; 4. borde ...
- php实现常驻进程 多进程监控
php都是通过crontabd定时脚本处理队列的,面试被问到php如何常驻进程进行处理队列,想了半天这样不知道是否是一种方式 <?php function logs(){ file_put_co ...
- [日常工作]Oracle新增数据文件的小知识点
1. 表空间是small file tablespace的 然后数据文件长到了32g左右之后无法再次扩充, 应用报错了 为了性能和最快的处理 使用语句 alter tablespace user ad ...
- React 组件
<!DOCTYPE html><html><head lang="en"> <meta charset="UTF-8" ...
- Wireshark协议分析工具应用
一.Wireshark简介与安装 Wireshark(前称Ethereal)是一个网络封包分析软件.网络封包分析软件的功能是撷取网络封包,并尽可能显示出最为详细的网络封包资料.Wireshark使用W ...
- 在做销售录入界面时,如何使用dbgrid?(50分)
给你段源码看一看用stringgird做得: procedure Tfrmingoods.adddata ; var i:integer; begin do begin ,i])=trim(goods ...
- Java之静态代码块
有一些情况下,有些代码需要在项目启动的时候就执行,则需要使用静态代码块,这种代码是主动执行的.Java中的静态代码块是在虚拟机加载类的时候,就执行的,而且只执行一次.如果static代码块有多个,JV ...
- caffe运行错误: im2col.cu:61] Check failed: error == cudaSuccess (8 vs. 0) invalid device function
错误: im2col.cu:61] Check failed: error == cudaSuccess (8 vs. 0) invalid device function 原因:由于Makefil ...
- 一本通1548【例 2】A Simple Problem with Integers
1548:[例 2]A Simple Problem with Integers 题目描述 这是一道模板题. 给定数列 a[1],a[2],…,a[n],你需要依次进行 q 个操作,操作有两类: 1 ...
- 转 PV、TPS、QPS 计算方法
PV.TPS.QPS是怎么计算出来的? QPS = req/sec = 请求数/秒 [QPS计算PV和机器的方式] QPS统计方式 [一般使用 http_load 进行统计]QPS = 总请求数 ...